HintMR: Eliciting Stronger Mathematical Reasoning in Small Language Models

Small language models (SLMs) often struggle with complex mathematical reasoning due to limited capacity to maintain long chains of intermediate steps and to recover from early errors. We address this challenge by introducing a hint-assisted reasoning framework that incrementally guides SLMs through multi-step mathematical problem solving. Our approach decomposes solutions into sequential reasoning steps and provides context-aware hints, where hints are generated by a separate SLM trained via distillation from a strong large language model. While the hint-generating SLM alone is not capable of solving the problems, its collaboration with a reasoning SLM enables effective guidance, forming a cooperative two-model system for reasoning. Each hint is generated conditionally on the problem statement and the accumulated reasoning history, providing stepwise, localized guidance without revealing full solutions. This reduces error propagation and allows the reasoning model to focus on manageable subproblems. Experiments across diverse mathematical benchmarks and models demonstrate that hint assistance consistently improves reasoning accuracy for SLMs, yielding substantial gains over standard prompting while preserving model efficiency. These results highlight that structured collaboration between SLMs-via hint generation and reasoning-offers an effective and lightweight mechanism for enhancing mathematical reasoning.

Rethinking Driving World Model as Synthetic Data Generator for Perception Tasks

Recent advancements in driving world models enable controllable generation of high-quality RGB videos or multimodal videos. Existing methods primarily focus on metrics related to generation quality and controllability. However, they often overlook the evaluation of downstream perception tasks, which are $\mathbf{really\ crucial}$ for the performance of autonomous driving. Existing methods usually leverage a training strategy that first pretrains on synthetic data and finetunes on real data, resulting in twice the epochs compared to the baseline (real data only). When we double the epochs in the baseline, the benefit of synthetic data becomes negligible. To thoroughly demonstrate the benefit of synthetic data, we introduce Dream4Drive, a novel synthetic data generation framework designed for enhancing the downstream perception tasks. Dream4Drive first decomposes the input video into several 3D-aware guidance maps and subsequently renders the 3D assets onto these guidance maps. Finally, the driving world model is fine-tuned to produce the edited, multi-view photorealistic videos, which can be used to train the downstream perception models. Dream4Drive enables unprecedented flexibility in generating multi-view corner cases at scale, significantly boosting corner case perception in autonomous driving. To facilitate future research, we also contribute a large-scale 3D asset dataset named DriveObj3D, covering the typical categories in driving scenarios and enabling diverse 3D-aware video editing. We conduct comprehensive experiments to show that Dream4Drive can effectively boost the performance of downstream perception models under various training epochs. Project: $\href{https://wm-research.github.io/Dream4Drive/}{this\ https\ URL}$

ReCogDrive: A Reinforced Cognitive Framework for End-to-End Autonomous Driving

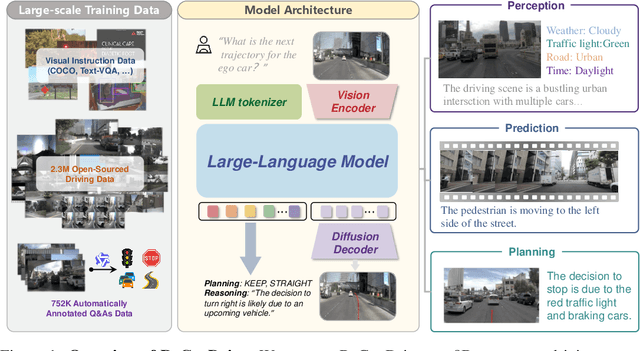
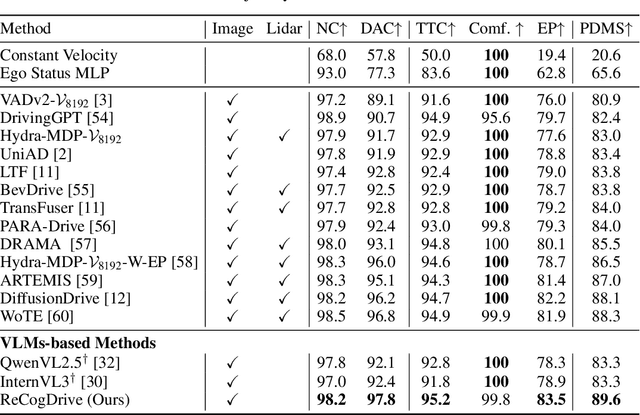
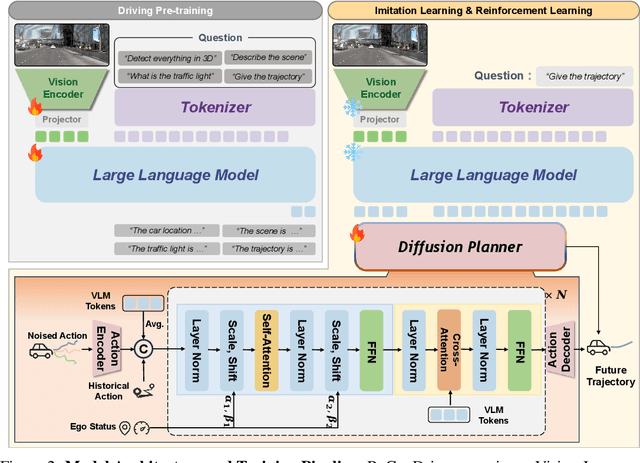
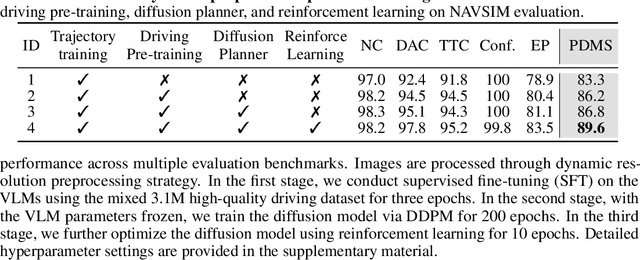
Although end-to-end autonomous driving has made remarkable progress, its performance degrades significantly in rare and long-tail scenarios. Recent approaches attempt to address this challenge by leveraging the rich world knowledge of Vision-Language Models (VLMs), but these methods suffer from several limitations: (1) a significant domain gap between the pre-training data of VLMs and real-world driving data, (2) a dimensionality mismatch between the discrete language space and the continuous action space, and (3) imitation learning tends to capture the average behavior present in the dataset, which may be suboptimal even dangerous. In this paper, we propose ReCogDrive, an autonomous driving system that integrates VLMs with diffusion planner, which adopts a three-stage paradigm for training. In the first stage, we use a large-scale driving question-answering datasets to train the VLMs, mitigating the domain discrepancy between generic content and real-world driving scenarios. In the second stage, we employ a diffusion-based planner to perform imitation learning, mapping representations from the latent language space to continuous driving actions. Finally, we fine-tune the diffusion planner using reinforcement learning with NAVSIM non-reactive simulator, enabling the model to generate safer, more human-like driving trajectories. We evaluate our approach on the planning-oriented NAVSIM benchmark, achieving a PDMS of 89.6 and setting a new state-of-the-art that surpasses the previous vision-only SOTA by 5.6 PDMS.

Genesis: Multimodal Driving Scene Generation with Spatio-Temporal and Cross-Modal Consistency

We present Genesis, a unified framework for joint generation of multi-view driving videos and LiDAR sequences with spatio-temporal and cross-modal consistency. Genesis employs a two-stage architecture that integrates a DiT-based video diffusion model with 3D-VAE encoding, and a BEV-aware LiDAR generator with NeRF-based rendering and adaptive sampling. Both modalities are directly coupled through a shared latent space, enabling coherent evolution across visual and geometric domains. To guide the generation with structured semantics, we introduce DataCrafter, a captioning module built on vision-language models that provides scene-level and instance-level supervision. Extensive experiments on the nuScenes benchmark demonstrate that Genesis achieves state-of-the-art performance across video and LiDAR metrics (FVD 16.95, FID 4.24, Chamfer 0.611), and benefits downstream tasks including segmentation and 3D detection, validating the semantic fidelity and practical utility of the generated data.

MARAGE: Transferable Multi-Model Adversarial Attack for Retrieval-Augmented Generation Data Extraction

Retrieval-Augmented Generation (RAG) offers a solution to mitigate hallucinations in Large Language Models (LLMs) by grounding their outputs to knowledge retrieved from external sources. The use of private resources and data in constructing these external data stores can expose them to risks of extraction attacks, in which attackers attempt to steal data from these private databases. Existing RAG extraction attacks often rely on manually crafted prompts, which limit their effectiveness. In this paper, we introduce a framework called MARAGE for optimizing an adversarial string that, when appended to user queries submitted to a target RAG system, causes outputs containing the retrieved RAG data verbatim. MARAGE leverages a continuous optimization scheme that integrates gradients from multiple models with different architectures simultaneously to enhance the transferability of the optimized string to unseen models. Additionally, we propose a strategy that emphasizes the initial tokens in the target RAG data, further improving the attack's generalizability. Evaluations show that MARAGE consistently outperforms both manual and optimization-based baselines across multiple LLMs and RAG datasets, while maintaining robust transferability to previously unseen models. Moreover, we conduct probing tasks to shed light on the reasons why MARAGE is more effective compared to the baselines and to analyze the impact of our approach on the model's internal state.

ANVIL: Anomaly-based Vulnerability Identification without Labelled Training Data

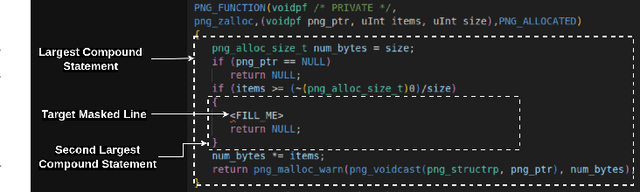
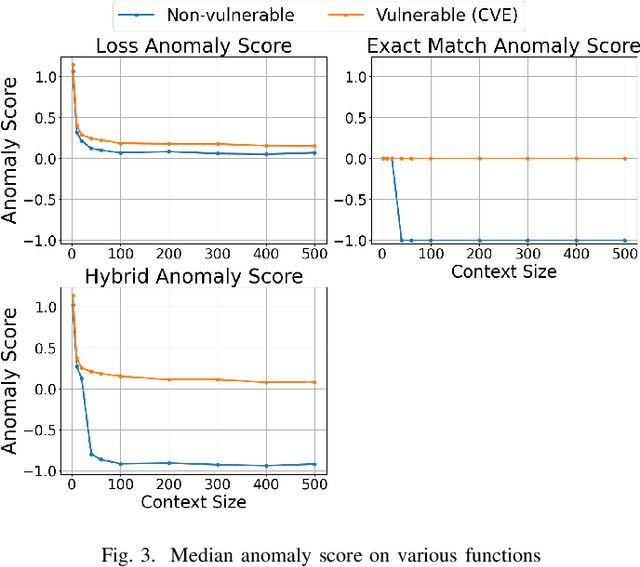
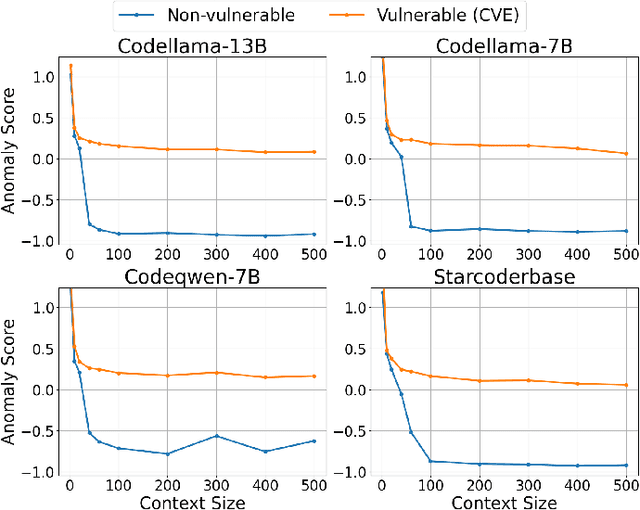
Supervised learning-based software vulnerability detectors often fall short due to the inadequate availability of labelled training data. In contrast, Large Language Models (LLMs) such as GPT-4, are not trained on labelled data, but when prompted to detect vulnerabilities, LLM prediction accuracy is only marginally better than random guessing. In this paper, we explore a different approach by reframing vulnerability detection as one of anomaly detection. Since the vast majority of code does not contain vulnerabilities and LLMs are trained on massive amounts of such code, vulnerable code can be viewed as an anomaly from the LLM's predicted code distribution, freeing the model from the need for labelled data to provide a learnable representation of vulnerable code. Leveraging this perspective, we demonstrate that LLMs trained for code generation exhibit a significant gap in prediction accuracy when prompted to reconstruct vulnerable versus non-vulnerable code. Using this insight, we implement ANVIL, a detector that identifies software vulnerabilities at line-level granularity. Our experiments explore the discriminating power of different anomaly scoring methods, as well as the sensitivity of ANVIL to context size. We also study the effectiveness of ANVIL on various LLM families, and conduct leakage experiments on vulnerabilities that were discovered after the knowledge cutoff of our evaluated LLMs. On a collection of vulnerabilities from the Magma benchmark, ANVIL outperforms state-of-the-art line-level vulnerability detectors, LineVul and LineVD, which have been trained with labelled data, despite ANVIL having never been trained with labelled vulnerabilities. Specifically, our approach achieves $1.62\times$ to $2.18\times$ better Top-5 accuracies and $1.02\times$ to $1.29\times$ times better ROC scores on line-level vulnerability detection tasks.

Finding Optimal Tangent Points for Reducing Distortions of Hard-label Attacks

One major problem in black-box adversarial attacks is the high query complexity in the hard-label attack setting, where only the top-1 predicted label is available. In this paper, we propose a novel geometric-based approach called Tangent Attack (TA), which identifies an optimal tangent point of a virtual hemisphere located on the decision boundary to reduce the distortion of the attack. Assuming the decision boundary is locally flat, we theoretically prove that the minimum $\ell_2$ distortion can be obtained by reaching the decision boundary along the tangent line passing through such tangent point in each iteration. To improve the robustness of our method, we further propose a generalized method which replaces the hemisphere with a semi-ellipsoid to adapt to curved decision boundaries. Our approach is free of hyperparameters and pre-training. Extensive experiments conducted on the ImageNet and CIFAR-10 datasets demonstrate that our approach can consume only a small number of queries to achieve the low-magnitude distortion. The implementation source code is released online at https://github.com/machanic/TangentAttack.

Robust High Dimensional Expectation Maximization Algorithm via Trimmed Hard Thresholding

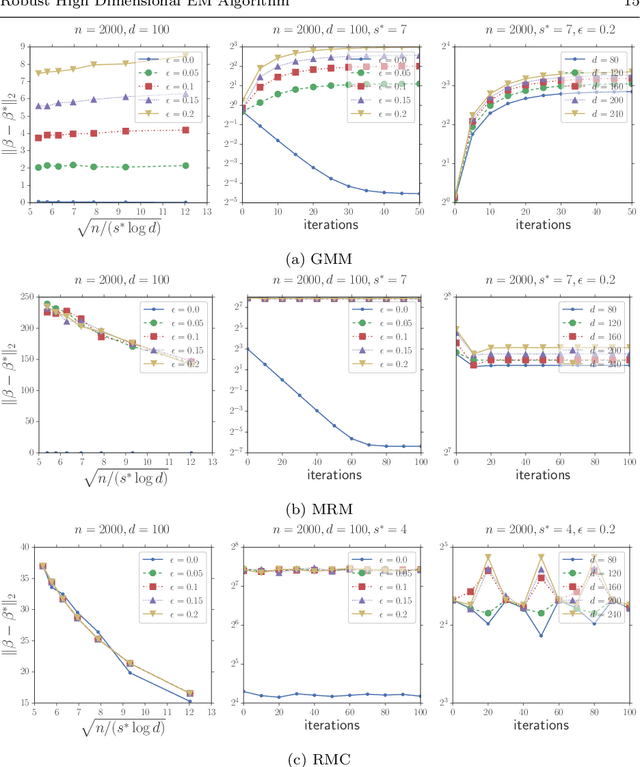
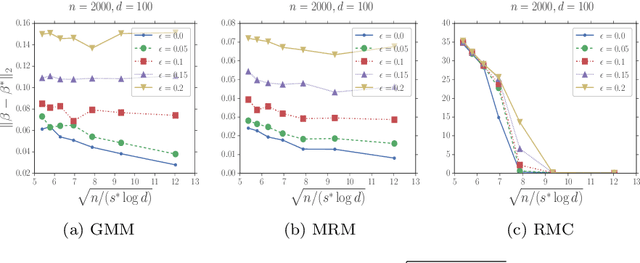
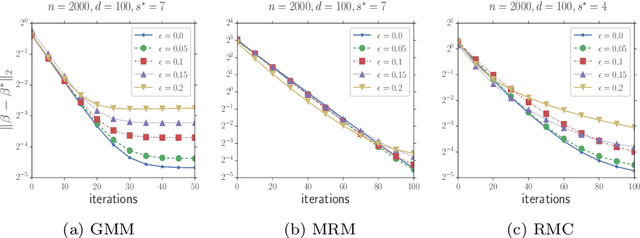
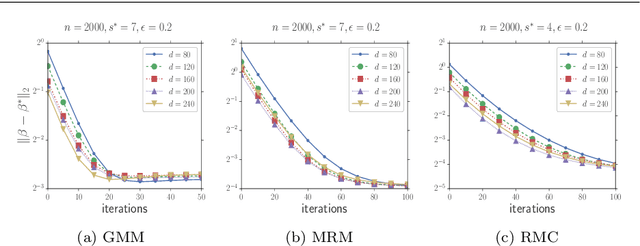
In this paper, we study the problem of estimating latent variable models with arbitrarily corrupted samples in high dimensional space ({\em i.e.,} $d\gg n$) where the underlying parameter is assumed to be sparse. Specifically, we propose a method called Trimmed (Gradient) Expectation Maximization which adds a trimming gradients step and a hard thresholding step to the Expectation step (E-step) and the Maximization step (M-step), respectively. We show that under some mild assumptions and with an appropriate initialization, the algorithm is corruption-proofing and converges to the (near) optimal statistical rate geometrically when the fraction of the corrupted samples $\epsilon$ is bounded by $ \tilde{O}(\frac{1}{\sqrt{n}})$. Moreover, we apply our general framework to three canonical models: mixture of Gaussians, mixture of regressions and linear regression with missing covariates. Our theory is supported by thorough numerical results.

Estimating Stochastic Linear Combination of Non-linear Regressions Efficiently and Scalably

Recently, many machine learning and statistical models such as non-linear regressions, the Single Index, Multi-index, Varying Coefficient Index Models and Two-layer Neural Networks can be reduced to or be seen as a special case of a new model which is called the \textit{Stochastic Linear Combination of Non-linear Regressions} model. However, due to the high non-convexity of the problem, there is no previous work study how to estimate the model. In this paper, we provide the first study on how to estimate the model efficiently and scalably. Specifically, we first show that with some mild assumptions, if the variate vector $x$ is multivariate Gaussian, then there is an algorithm whose output vectors have $\ell_2$-norm estimation errors of $O(\sqrt{\frac{p}{n}})$ with high probability, where $p$ is the dimension of $x$ and $n$ is the number of samples. The key idea of the proof is based on an observation motived by the Stein's lemma. Then we extend our result to the case where $x$ is bounded and sub-Gaussian using the zero-bias transformation, which could be seen as a generalization of the classic Stein's lemma. We also show that with some additional assumptions there is an algorithm whose output vectors have $\ell_\infty$-norm estimation errors of $O(\frac{1}{\sqrt{p}}+\sqrt{\frac{p}{n}})$ with high probability. We also provide a concrete example to show that there exists some link function which satisfies the previous assumptions. Finally, for both Gaussian and sub-Gaussian cases we propose a faster sub-sampling based algorithm and show that when the sub-sample sizes are large enough then the estimation errors will not be sacrificed by too much. Experiments for both cases support our theoretical results. To the best of our knowledge, this is the first work that studies and provides theoretical guarantees for the stochastic linear combination of non-linear regressions model.

Consistent $k$-Median: Simpler, Better and Robust

In this paper we introduce and study the online consistent $k$-clustering with outliers problem, generalizing the non-outlier version of the problem studied in [Lattanzi-Vassilvitskii, ICML17]. We show that a simple local-search based online algorithm can give a bicriteria constant approximation for the problem with $O(k^2 \log^2 (nD))$ swaps of medians (recourse) in total, where $D$ is the diameter of the metric. When restricted to the problem without outliers, our algorithm is simpler, deterministic and gives better approximation ratio and recourse, compared to that of [Lattanzi-Vassilvitskii, ICML17].