Hybrid Forecasting of Chaotic Processes: Using Machine Learning in Conjunction with a Knowledge-Based Model
Paper and Code
Mar 09, 2018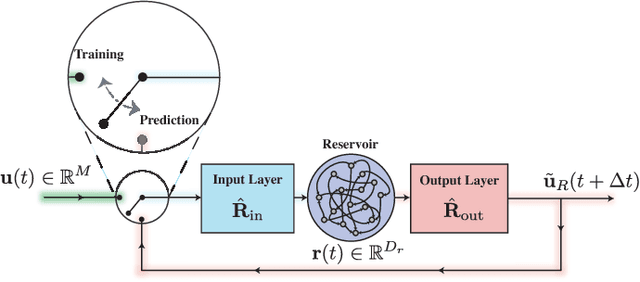
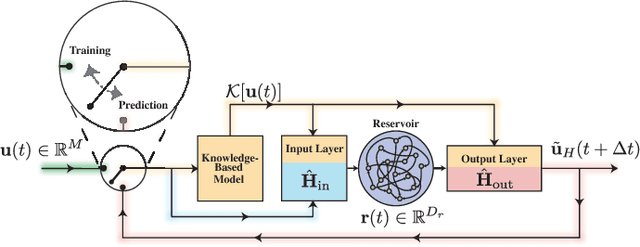
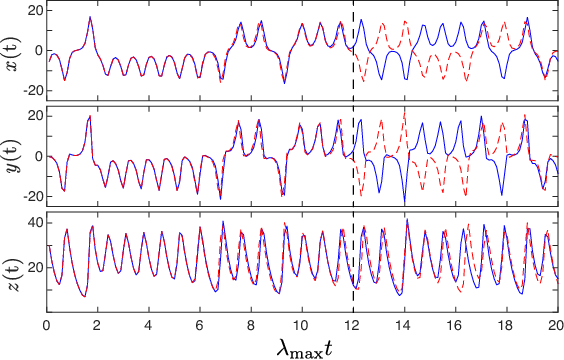
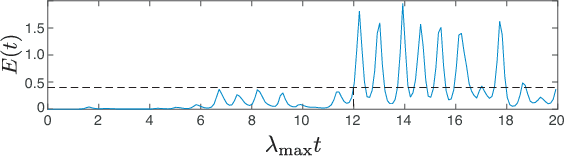
A model-based approach to forecasting chaotic dynamical systems utilizes knowledge of the physical processes governing the dynamics to build an approximate mathematical model of the system. In contrast, machine learning techniques have demonstrated promising results for forecasting chaotic systems purely from past time series measurements of system state variables (training data), without prior knowledge of the system dynamics. The motivation for this paper is the potential of machine learning for filling in the gaps in our underlying mechanistic knowledge that cause widely-used knowledge-based models to be inaccurate. Thus we here propose a general method that leverages the advantages of these two approaches by combining a knowledge-based model and a machine learning technique to build a hybrid forecasting scheme. Potential applications for such an approach are numerous (e.g., improving weather forecasting). We demonstrate and test the utility of this approach using a particular illustrative version of a machine learning known as reservoir computing, and we apply the resulting hybrid forecaster to a low-dimensional chaotic system, as well as to a high-dimensional spatiotemporal chaotic system. These tests yield extremely promising results in that our hybrid technique is able to accurately predict for a much longer period of time than either its machine-learning component or its model-based component alone.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge