Characterizing control between interacting subsystems with deep Jacobian estimation

Biological function arises through the dynamical interactions of multiple subsystems, including those between brain areas, within gene regulatory networks, and more. A common approach to understanding these systems is to model the dynamics of each subsystem and characterize communication between them. An alternative approach is through the lens of control theory: how the subsystems control one another. This approach involves inferring the directionality, strength, and contextual modulation of control between subsystems. However, methods for understanding subsystem control are typically linear and cannot adequately describe the rich contextual effects enabled by nonlinear complex systems. To bridge this gap, we devise a data-driven nonlinear control-theoretic framework to characterize subsystem interactions via the Jacobian of the dynamics. We address the challenge of learning Jacobians from time-series data by proposing the JacobianODE, a deep learning method that leverages properties of the Jacobian to directly estimate it for arbitrary dynamical systems from data alone. We show that JacobianODEs outperform existing Jacobian estimation methods on challenging systems, including high-dimensional chaos. Applying our approach to a multi-area recurrent neural network (RNN) trained on a working memory selection task, we show that the "sensory" area gains greater control over the "cognitive" area over learning. Furthermore, we leverage the JacobianODE to directly control the trained RNN, enabling precise manipulation of its behavior. Our work lays the foundation for a theoretically grounded and data-driven understanding of interactions among biological subsystems.

Bridging Associative Memory and Probabilistic Modeling

Associative memory and probabilistic modeling are two fundamental topics in artificial intelligence. The first studies recurrent neural networks designed to denoise, complete and retrieve data, whereas the second studies learning and sampling from probability distributions. Based on the observation that associative memory's energy functions can be seen as probabilistic modeling's negative log likelihoods, we build a bridge between the two that enables useful flow of ideas in both directions. We showcase four examples: First, we propose new energy-based models that flexibly adapt their energy functions to new in-context datasets, an approach we term \textit{in-context learning of energy functions}. Second, we propose two new associative memory models: one that dynamically creates new memories as necessitated by the training data using Bayesian nonparametrics, and another that explicitly computes proportional memory assignments using the evidence lower bound. Third, using tools from associative memory, we analytically and numerically characterize the memory capacity of Gaussian kernel density estimators, a widespread tool in probababilistic modeling. Fourth, we study a widespread implementation choice in transformers -- normalization followed by self attention -- to show it performs clustering on the hypersphere. Altogether, this work urges further exchange of useful ideas between these two continents of artificial intelligence.

Content addressable memory without catastrophic forgetting by heteroassociation with a fixed scaffold

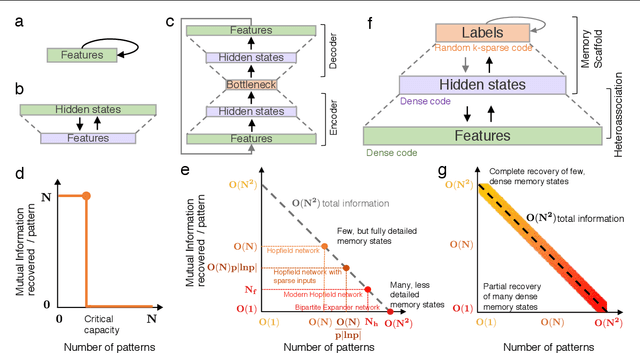
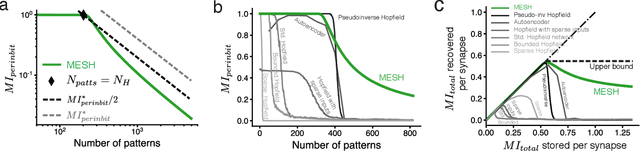
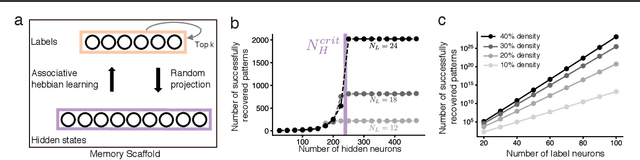
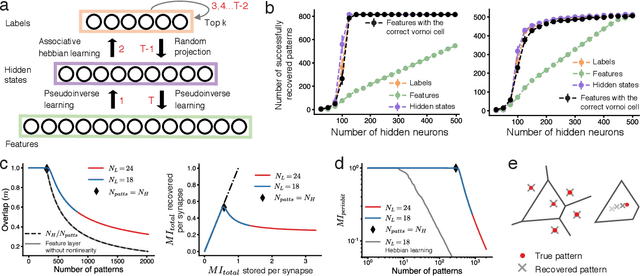
Content-addressable memory (CAM) networks, so-called because stored items can be recalled by partial or corrupted versions of the items, exhibit near-perfect recall of a small number of information-dense patterns below capacity and a `memory cliff' beyond, such that inserting a single additional pattern results in catastrophic forgetting of all stored patterns. We propose a novel ANN architecture, Memory Scaffold with Heteroassociation (MESH), that gracefully trades-off pattern richness with pattern number to generate a CAM continuum without a memory cliff: Small numbers of patterns are stored with complete information recovery matching standard CAMs, while inserting more patterns still results in partial recall of every pattern, with an information per pattern that scales inversely with the number of patterns. Motivated by the architecture of the Entorhinal-Hippocampal memory circuit in the brain, MESH is a tripartite architecture with pairwise interactions that uses a predetermined set of internally stabilized states together with heteroassociation between the internal states and arbitrary external patterns. We show analytically and experimentally that MESH nearly saturates the total information bound (given by the number of synapses) for CAM networks, invariant of the number of stored patterns, outperforming all existing CAM models.

Hybrid Forecasting of Chaotic Processes: Using Machine Learning in Conjunction with a Knowledge-Based Model

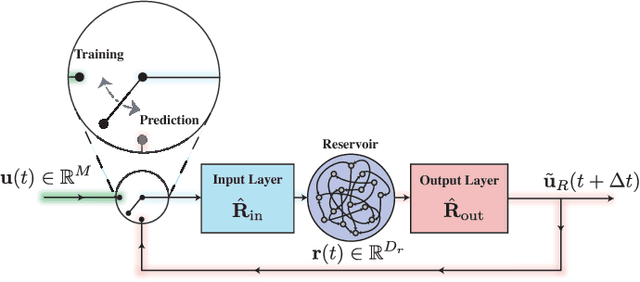
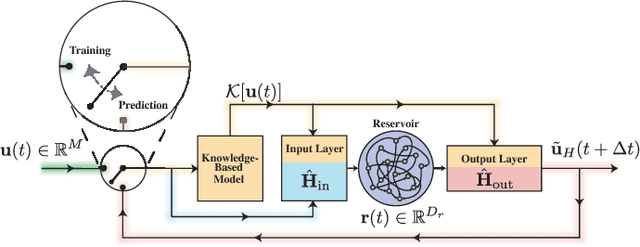
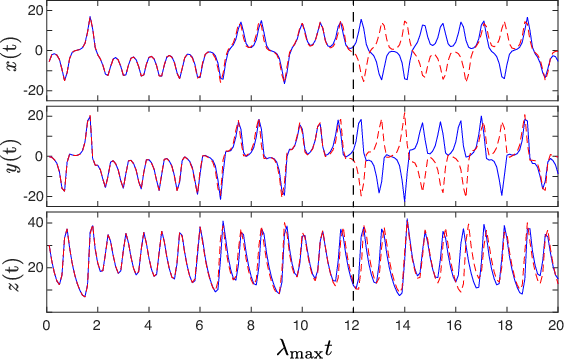
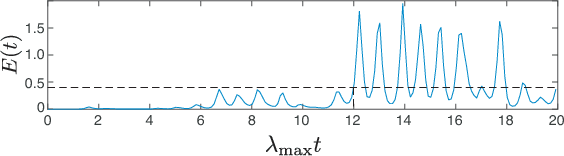
A model-based approach to forecasting chaotic dynamical systems utilizes knowledge of the physical processes governing the dynamics to build an approximate mathematical model of the system. In contrast, machine learning techniques have demonstrated promising results for forecasting chaotic systems purely from past time series measurements of system state variables (training data), without prior knowledge of the system dynamics. The motivation for this paper is the potential of machine learning for filling in the gaps in our underlying mechanistic knowledge that cause widely-used knowledge-based models to be inaccurate. Thus we here propose a general method that leverages the advantages of these two approaches by combining a knowledge-based model and a machine learning technique to build a hybrid forecasting scheme. Potential applications for such an approach are numerous (e.g., improving weather forecasting). We demonstrate and test the utility of this approach using a particular illustrative version of a machine learning known as reservoir computing, and we apply the resulting hybrid forecaster to a low-dimensional chaotic system, as well as to a high-dimensional spatiotemporal chaotic system. These tests yield extremely promising results in that our hybrid technique is able to accurately predict for a much longer period of time than either its machine-learning component or its model-based component alone.