Content addressable memory without catastrophic forgetting by heteroassociation with a fixed scaffold

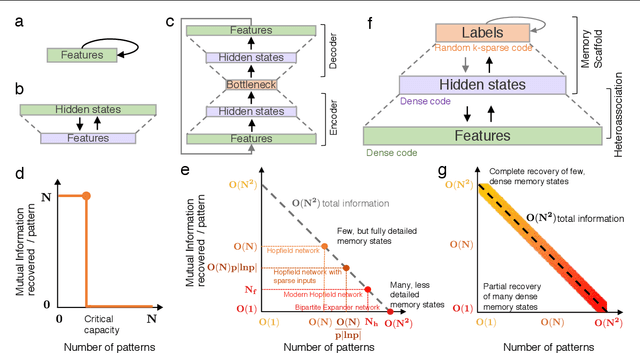
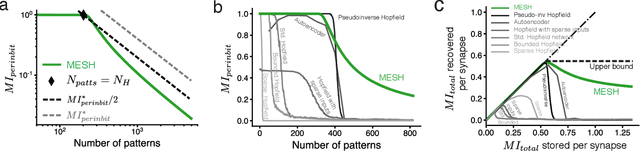
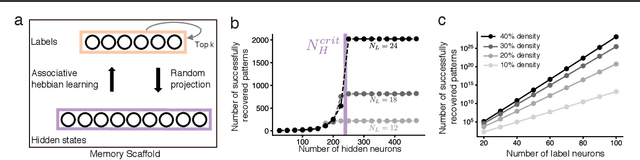
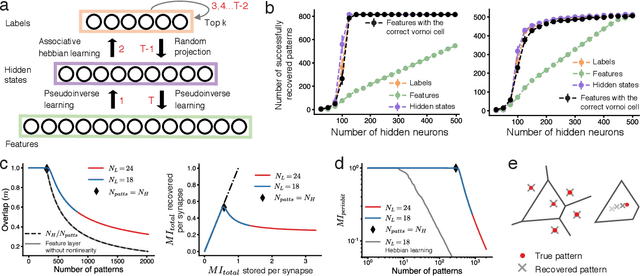
Content-addressable memory (CAM) networks, so-called because stored items can be recalled by partial or corrupted versions of the items, exhibit near-perfect recall of a small number of information-dense patterns below capacity and a `memory cliff' beyond, such that inserting a single additional pattern results in catastrophic forgetting of all stored patterns. We propose a novel ANN architecture, Memory Scaffold with Heteroassociation (MESH), that gracefully trades-off pattern richness with pattern number to generate a CAM continuum without a memory cliff: Small numbers of patterns are stored with complete information recovery matching standard CAMs, while inserting more patterns still results in partial recall of every pattern, with an information per pattern that scales inversely with the number of patterns. Motivated by the architecture of the Entorhinal-Hippocampal memory circuit in the brain, MESH is a tripartite architecture with pairwise interactions that uses a predetermined set of internally stabilized states together with heteroassociation between the internal states and arbitrary external patterns. We show analytically and experimentally that MESH nearly saturates the total information bound (given by the number of synapses) for CAM networks, invariant of the number of stored patterns, outperforming all existing CAM models.