Characterizing control between interacting subsystems with deep Jacobian estimation

Biological function arises through the dynamical interactions of multiple subsystems, including those between brain areas, within gene regulatory networks, and more. A common approach to understanding these systems is to model the dynamics of each subsystem and characterize communication between them. An alternative approach is through the lens of control theory: how the subsystems control one another. This approach involves inferring the directionality, strength, and contextual modulation of control between subsystems. However, methods for understanding subsystem control are typically linear and cannot adequately describe the rich contextual effects enabled by nonlinear complex systems. To bridge this gap, we devise a data-driven nonlinear control-theoretic framework to characterize subsystem interactions via the Jacobian of the dynamics. We address the challenge of learning Jacobians from time-series data by proposing the JacobianODE, a deep learning method that leverages properties of the Jacobian to directly estimate it for arbitrary dynamical systems from data alone. We show that JacobianODEs outperform existing Jacobian estimation methods on challenging systems, including high-dimensional chaos. Applying our approach to a multi-area recurrent neural network (RNN) trained on a working memory selection task, we show that the "sensory" area gains greater control over the "cognitive" area over learning. Furthermore, we leverage the JacobianODE to directly control the trained RNN, enabling precise manipulation of its behavior. Our work lays the foundation for a theoretically grounded and data-driven understanding of interactions among biological subsystems.

Growing Brains: Co-emergence of Anatomical and Functional Modularity in Recurrent Neural Networks

Recurrent neural networks (RNNs) trained on compositional tasks can exhibit functional modularity, in which neurons can be clustered by activity similarity and participation in shared computational subtasks. Unlike brains, these RNNs do not exhibit anatomical modularity, in which functional clustering is correlated with strong recurrent coupling and spatial localization of functional clusters. Contrasting with functional modularity, which can be ephemerally dependent on the input, anatomically modular networks form a robust substrate for solving the same subtasks in the future. To examine whether it is possible to grow brain-like anatomical modularity, we apply a recent machine learning method, brain-inspired modular training (BIMT), to a network being trained to solve a set of compositional cognitive tasks. We find that functional and anatomical clustering emerge together, such that functionally similar neurons also become spatially localized and interconnected. Moreover, compared to standard $L_1$ or no regularization settings, the model exhibits superior performance by optimally balancing task performance and network sparsity. In addition to achieving brain-like organization in RNNs, our findings also suggest that BIMT holds promise for applications in neuromorphic computing and enhancing the interpretability of neural network architectures.

Content addressable memory without catastrophic forgetting by heteroassociation with a fixed scaffold

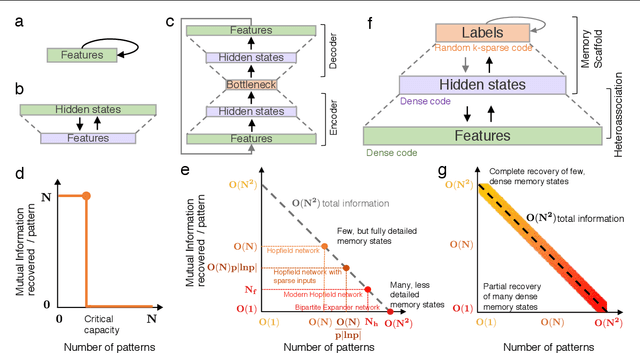
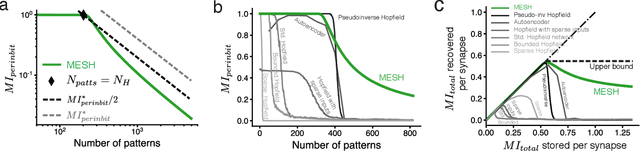
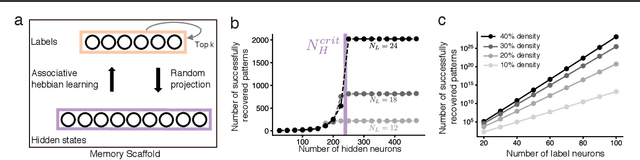
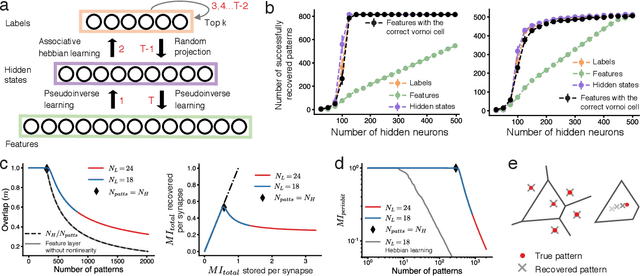
Content-addressable memory (CAM) networks, so-called because stored items can be recalled by partial or corrupted versions of the items, exhibit near-perfect recall of a small number of information-dense patterns below capacity and a `memory cliff' beyond, such that inserting a single additional pattern results in catastrophic forgetting of all stored patterns. We propose a novel ANN architecture, Memory Scaffold with Heteroassociation (MESH), that gracefully trades-off pattern richness with pattern number to generate a CAM continuum without a memory cliff: Small numbers of patterns are stored with complete information recovery matching standard CAMs, while inserting more patterns still results in partial recall of every pattern, with an information per pattern that scales inversely with the number of patterns. Motivated by the architecture of the Entorhinal-Hippocampal memory circuit in the brain, MESH is a tripartite architecture with pairwise interactions that uses a predetermined set of internally stabilized states together with heteroassociation between the internal states and arbitrary external patterns. We show analytically and experimentally that MESH nearly saturates the total information bound (given by the number of synapses) for CAM networks, invariant of the number of stored patterns, outperforming all existing CAM models.