Characterizing control between interacting subsystems with deep Jacobian estimation

Biological function arises through the dynamical interactions of multiple subsystems, including those between brain areas, within gene regulatory networks, and more. A common approach to understanding these systems is to model the dynamics of each subsystem and characterize communication between them. An alternative approach is through the lens of control theory: how the subsystems control one another. This approach involves inferring the directionality, strength, and contextual modulation of control between subsystems. However, methods for understanding subsystem control are typically linear and cannot adequately describe the rich contextual effects enabled by nonlinear complex systems. To bridge this gap, we devise a data-driven nonlinear control-theoretic framework to characterize subsystem interactions via the Jacobian of the dynamics. We address the challenge of learning Jacobians from time-series data by proposing the JacobianODE, a deep learning method that leverages properties of the Jacobian to directly estimate it for arbitrary dynamical systems from data alone. We show that JacobianODEs outperform existing Jacobian estimation methods on challenging systems, including high-dimensional chaos. Applying our approach to a multi-area recurrent neural network (RNN) trained on a working memory selection task, we show that the "sensory" area gains greater control over the "cognitive" area over learning. Furthermore, we leverage the JacobianODE to directly control the trained RNN, enabling precise manipulation of its behavior. Our work lays the foundation for a theoretically grounded and data-driven understanding of interactions among biological subsystems.

Differentiable Optimization of Similarity Scores Between Models and Brains

What metrics should guide the development of more realistic models of the brain? One proposal is to quantify the similarity between models and brains using methods such as linear regression, Centered Kernel Alignment (CKA), and angular Procrustes distance. To better understand the limitations of these similarity measures we analyze neural activity recorded in five experiments on nonhuman primates, and optimize synthetic datasets to become more similar to these neural recordings. How similar can these synthetic datasets be to neural activity while failing to encode task relevant variables? We find that some measures like linear regression and CKA, differ from angular Procrustes, and yield high similarity scores even when task relevant variables cannot be linearly decoded from the synthetic datasets. Synthetic datasets optimized to maximize similarity scores initially learn the first principal component of the target dataset, but angular Procrustes captures higher variance dimensions much earlier than methods like linear regression and CKA. We show in both theory and simulations how these scores change when different principal components are perturbed. And finally, we jointly optimize multiple similarity scores to find their allowed ranges, and show that a high angular Procrustes similarity, for example, implies a high CKA score, but not the converse.

Torus Graphs for Multivariate Phase Coupling Analysis

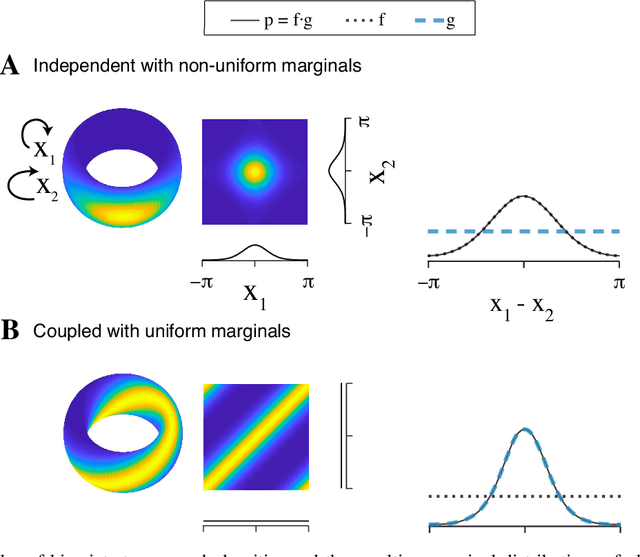
Angular measurements are often modeled as circular random variables, where there are natural circular analogues of moments, including correlation. Because a product of circles is a torus, a d-dimensional vector of circular random variables lies on a d-dimensional torus. For such vectors we present here a class of graphical models, which we call torus graphs, based on the full exponential family with pairwise interactions. The topological distinction between a torus and Euclidean space has several important consequences. Our development was motivated by the problem of identifying phase coupling among oscillatory signals recorded from multiple electrodes in the brain: oscillatory phases across electrodes might tend to advance or recede together, indicating coordination across brain areas. The data analyzed here consisted of 24 phase angles measured repeatedly across 840 experimental trials (replications) during a memory task, where the electrodes were in 4 distinct brain regions, all known to be active while memories are being stored or retrieved. In realistic numerical simulations, we found that a standard pairwise assessment, known as phase locking value, is unable to describe multivariate phase interactions, but that torus graphs can accurately identify conditional associations. Torus graphs generalize several more restrictive approaches that have appeared in various scientific literatures, and produced intuitive results in the data we analyzed. Torus graphs thus unify multivariate analysis of circular data and present fertile territory for future research.