Attractor reconstruction with reservoir computers: The effect of the reservoir's conditional Lyapunov exponents on faithful attractor reconstruction

Reservoir computing is a machine learning technique which has been shown to be able to replicate the chaotic attractor, including the fractal dimension and the entire Lyapunov spectrum, of the dynamical system on which it is trained. We quantitatively relate the generalized synchronization dynamics of a driven reservoir computer during the training stage to the performance of the autonomous reservoir computer at the attractor reconstruction task. We show that, for successful attractor reconstruction and Lyapunov exponent estimation, the largest conditional Lyapunov exponent of the driven reservoir must be significantly smaller (more negative) than the smallest (most negative) Lyapunov exponent of the true system. We find that the maximal conditional Lyapunov exponent of the reservoir depends strongly on the spectral radius of the reservoir adjacency matrix, and therefore, for attractor reconstruction and Lyapunov exponent estimation, small spectral radius reservoir computers perform better in general. Our arguments are supported by numerical examples on well-known chaotic systems.

Reservoir Computing with Noise

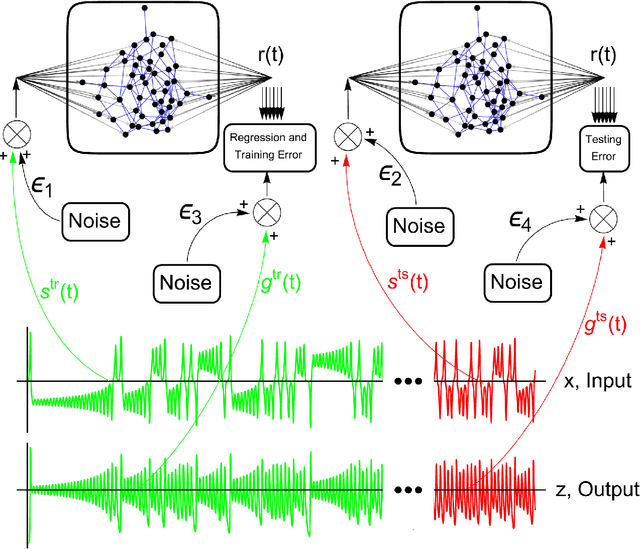
This paper investigates in detail the effects of noise on the performance of reservoir computing. We focus on an application in which reservoir computers are used to learn the relationship between different state variables of a chaotic system. We recognize that noise can affect differently the training and testing phases. We find that the best performance of the reservoir is achieved when the strength of the noise that affects the input signal in the training phase equals the strength of the noise that affects the input signal in the testing phase. For all the cases we examined, we found that a good remedy to noise is to low-pass filter the input and the training/testing signals; this typically preserves the performance of the reservoir, while reducing the undesired effects of noise.

Optimizing time-shifts for reservoir computing using a rank-revealing QR algorithm

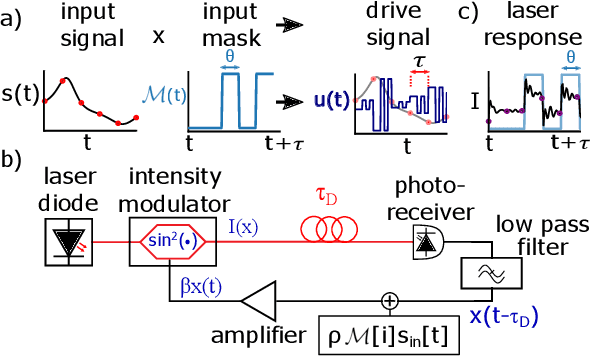
Reservoir computing is a recurrent neural network paradigm in which only the output layer is trained. Recently, it was demonstrated that adding time-shifts to the signals generated by a reservoir can provide large improvements in performance accuracy. In this work, we present a technique to choose the optimal time shifts. Our technique maximizes the rank of the reservoir matrix using a rank-revealing QR algorithm and is not task dependent. Further, our technique does not require a model of the system, and therefore is directly applicable to analog hardware reservoir computers. We demonstrate our time-shift optimization technique on two types of reservoir computer: one based on an opto-electronic oscillator and the traditional recurrent network with a $tanh$ activation function. We find that our technique provides improved accuracy over random time-shift selection in essentially all cases.

Time Shifts to Reduce the Size of Reservoir Computers

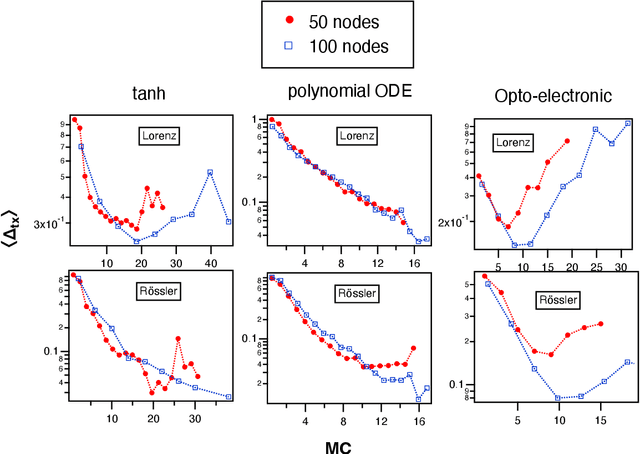
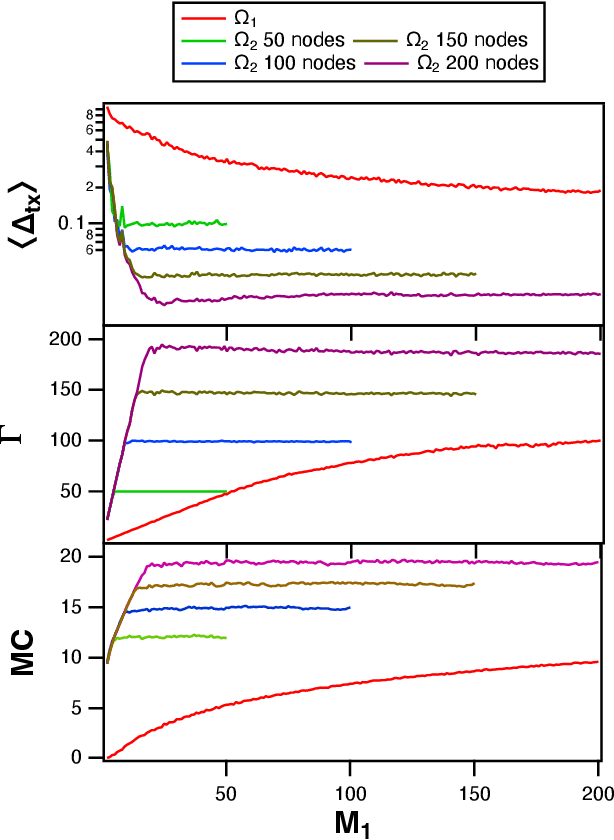
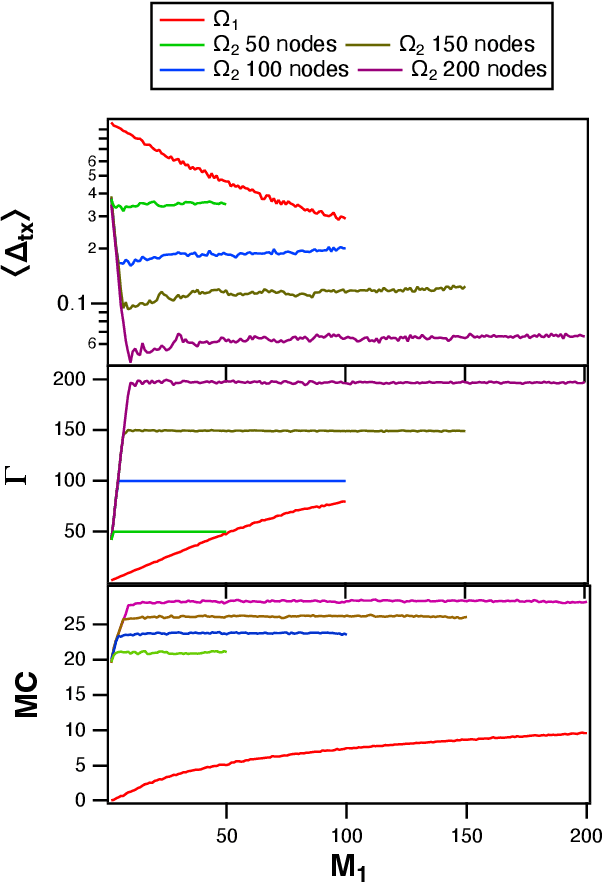
A reservoir computer is a type of dynamical system arranged to do computation. Typically, a reservoir computer is constructed by connecting a large number of nonlinear nodes in a network that includes recurrent connections. In order to achieve accurate results, the reservoir usually contains hundreds to thousands of nodes. This high dimensionality makes it difficult to analyze the reservoir computer using tools from dynamical systems theory. Additionally, the need to create and connect large numbers of nonlinear nodes makes it difficult to design and build analog reservoir computers that can be faster and consume less power than digital reservoir computers. We demonstrate here that a reservoir computer may be divided into two parts; a small set of nonlinear nodes (the reservoir), and a separate set of time-shifted reservoir output signals. The time-shifted output signals serve to increase the rank and memory of the reservoir computer, and the set of nonlinear nodes may create an embedding of the input dynamical system. We use this time-shifting technique to obtain excellent performance from an opto-electronic delay-based reservoir computer with only a small number of virtual nodes. Because only a few nonlinear nodes are required, construction of a reservoir computer becomes much easier, and delay-based reservoir computers can operate at much higher speeds.

Link inference of noisy delay-coupled networks: Machine learning and opto-electronic experimental tests

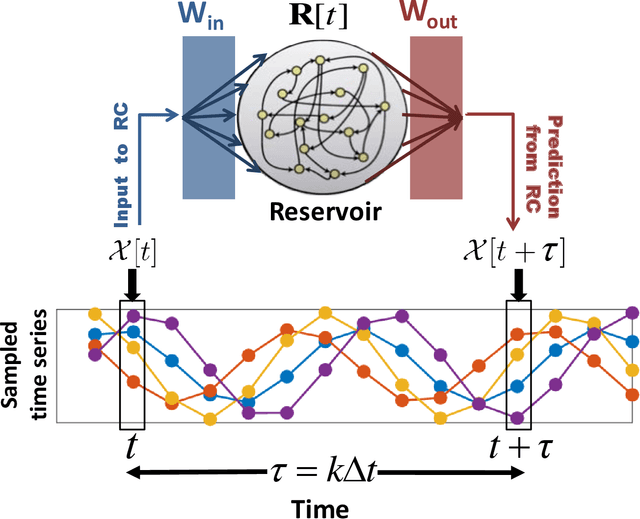
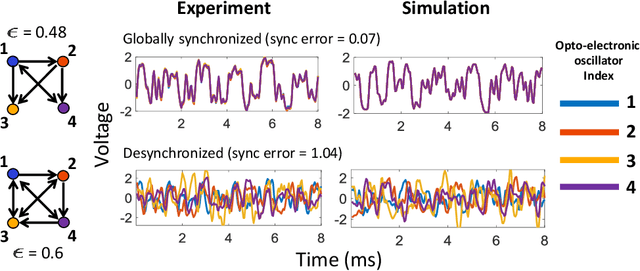
We devise a machine learning technique to solve the general problem of inferring network links that have time-delays. The goal is to do this purely from time-series data of the network nodal states. This task has applications in fields ranging from applied physics and engineering to neuroscience and biology. To achieve this, we first train a type of machine learning system known as reservoir computing to mimic the dynamics of the unknown network. We formulate and test a technique that uses the trained parameters of the reservoir system output layer to deduce an estimate of the unknown network structure. Our technique, by its nature, is non-invasive, but is motivated by the widely-used invasive network inference method whereby the responses to active perturbations applied to the network are observed and employed to infer network links (e.g., knocking down genes to infer gene regulatory networks). We test this technique on experimental and simulated data from delay-coupled opto-electronic oscillator networks. We show that the technique often yields very good results particularly if the system does not exhibit synchrony. We also find that the presence of dynamical noise can strikingly enhance the accuracy and ability of our technique, especially in networks that exhibit synchrony.