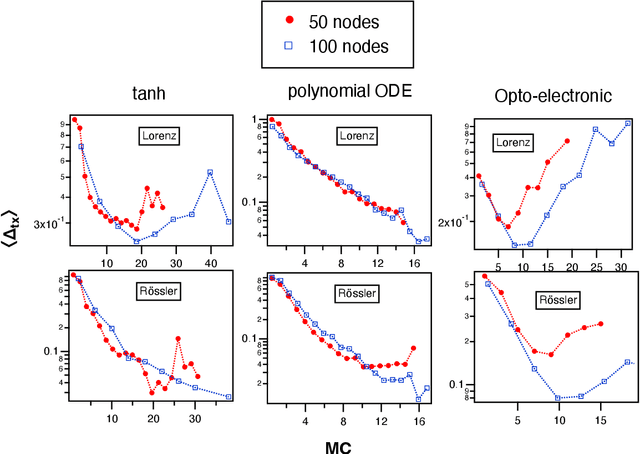
Optimizing time-shifts for reservoir computing using a rank-revealing QR algorithm

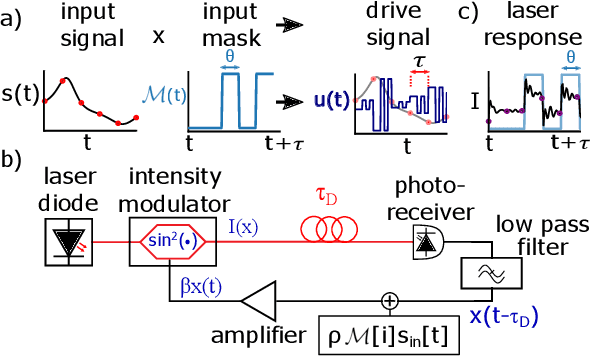
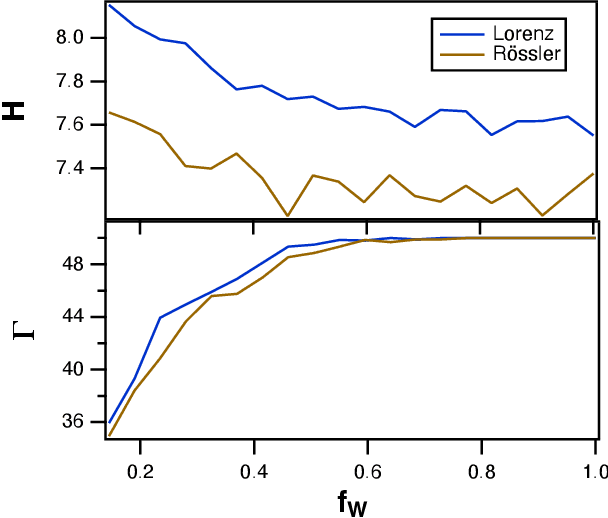
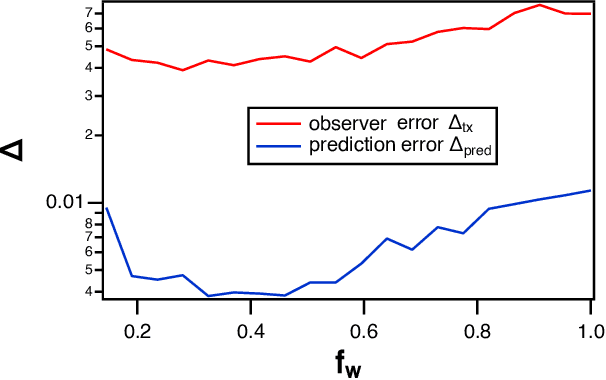
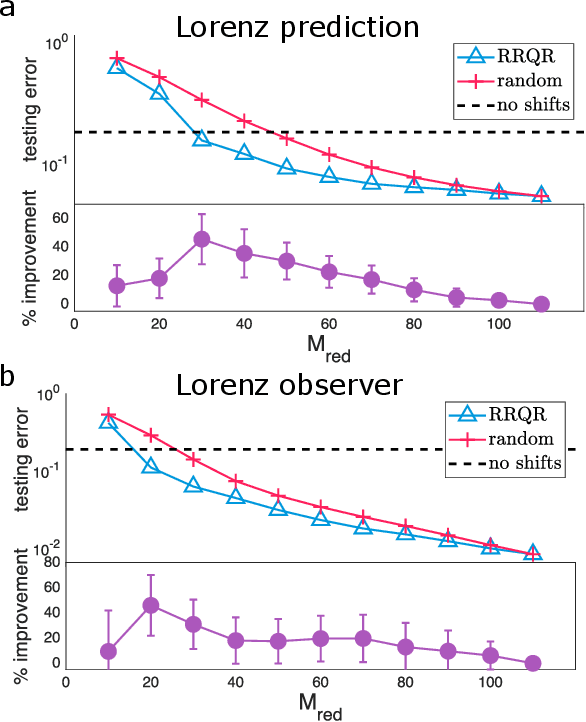
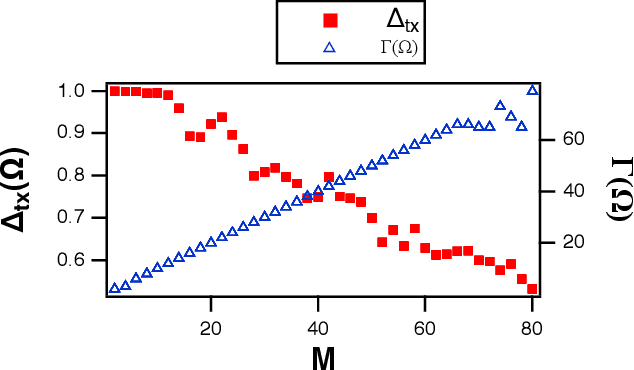
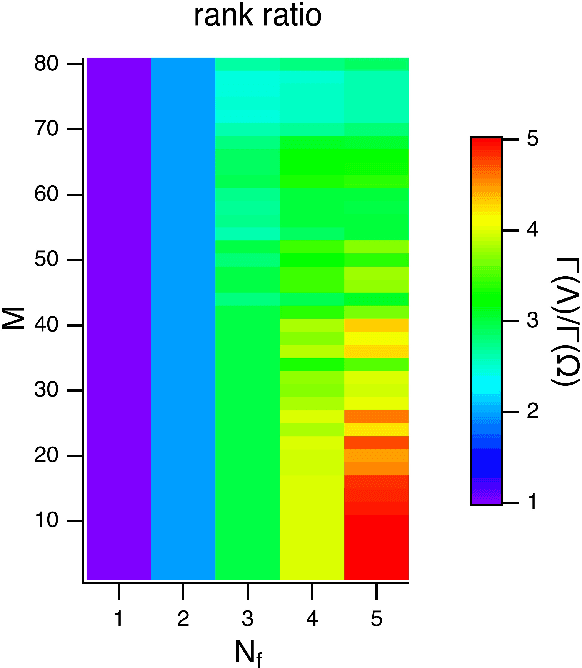
Reservoir computing is a recurrent neural network paradigm in which only the output layer is trained. Recently, it was demonstrated that adding time-shifts to the signals generated by a reservoir can provide large improvements in performance accuracy. In this work, we present a technique to choose the optimal time shifts. Our technique maximizes the rank of the reservoir matrix using a rank-revealing QR algorithm and is not task dependent. Further, our technique does not require a model of the system, and therefore is directly applicable to analog hardware reservoir computers. We demonstrate our time-shift optimization technique on two types of reservoir computer: one based on an opto-electronic oscillator and the traditional recurrent network with a $tanh$ activation function. We find that our technique provides improved accuracy over random time-shift selection in essentially all cases.

Time Shifts to Reduce the Size of Reservoir Computers

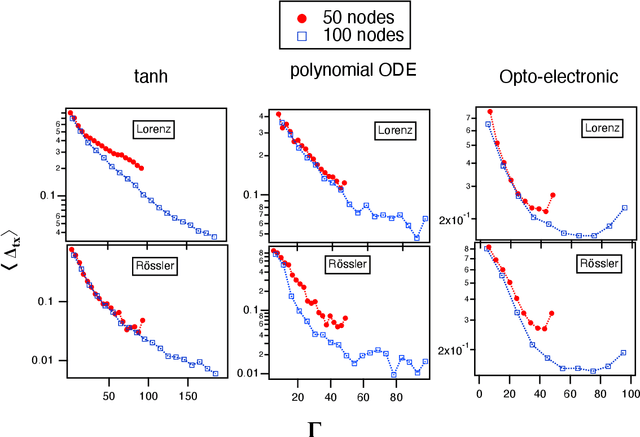
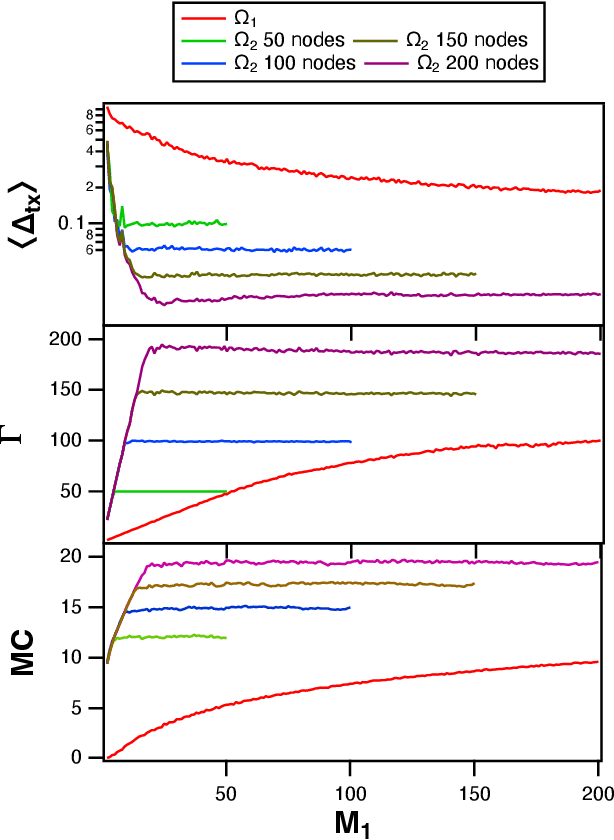
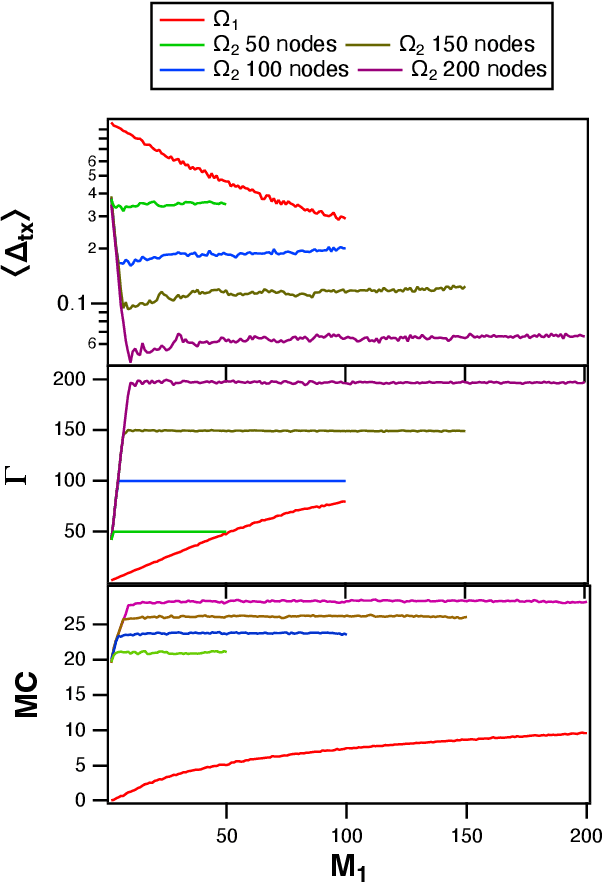
A reservoir computer is a type of dynamical system arranged to do computation. Typically, a reservoir computer is constructed by connecting a large number of nonlinear nodes in a network that includes recurrent connections. In order to achieve accurate results, the reservoir usually contains hundreds to thousands of nodes. This high dimensionality makes it difficult to analyze the reservoir computer using tools from dynamical systems theory. Additionally, the need to create and connect large numbers of nonlinear nodes makes it difficult to design and build analog reservoir computers that can be faster and consume less power than digital reservoir computers. We demonstrate here that a reservoir computer may be divided into two parts; a small set of nonlinear nodes (the reservoir), and a separate set of time-shifted reservoir output signals. The time-shifted output signals serve to increase the rank and memory of the reservoir computer, and the set of nonlinear nodes may create an embedding of the input dynamical system. We use this time-shifting technique to obtain excellent performance from an opto-electronic delay-based reservoir computer with only a small number of virtual nodes. Because only a few nonlinear nodes are required, construction of a reservoir computer becomes much easier, and delay-based reservoir computers can operate at much higher speeds.

Light in the Larynx: a Miniaturized Robotic Optical Fiber for In-office Laser Surgery of the Vocal Folds

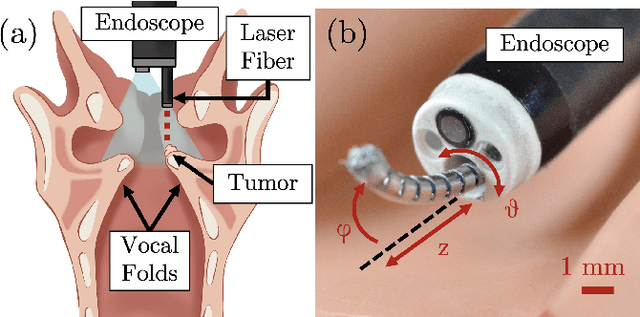
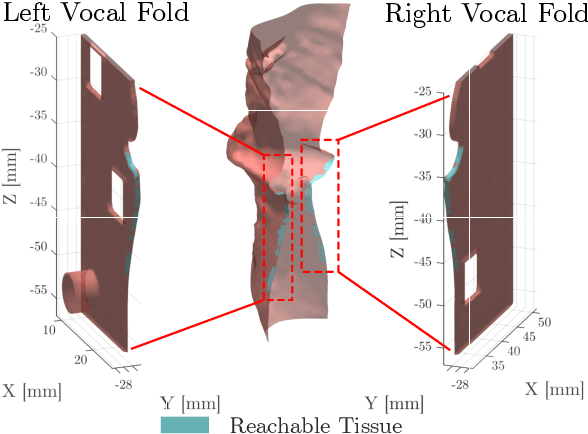
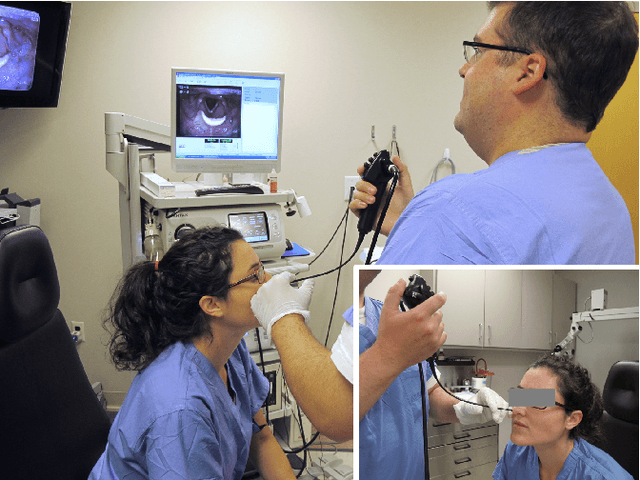
This letter reports the design, construction, and experimental validation of a novel hand-held robot for in-office laser surgery of the vocal folds. In-office endoscopic laser surgery is an emerging trend in Laryngology: It promises to deliver the same patient outcomes of traditional surgical treatment (i.e., in the operating room), at a fraction of the cost. Unfortunately, office procedures can be challenging to perform; the optical fibers used for laser delivery can only emit light forward in a line-of-sight fashion, which severely limits anatomical access. The robot we present in this letter aims to overcome these challenges. The end effector of the robot is a steerable laser fiber, created through the combination of a thin optical fiber (0.225 mm) with a tendon-actuated Nickel-Titanium notched sheath that provides bending. This device can be seamlessly used with most commercially available endoscopes, as it is sufficiently small (1.1 mm) to pass through a working channel. To control the fiber, we propose a compact actuation unit that can be mounted on top of the endoscope handle, so that, during a procedure, the operating physician can operate both the endoscope and the steerable fiber with a single hand. We report simulation and phantom experiments demonstrating that the proposed device substantially enhances surgical access compared to current clinical fibers.

Optimizing Memory in Reservoir Computers

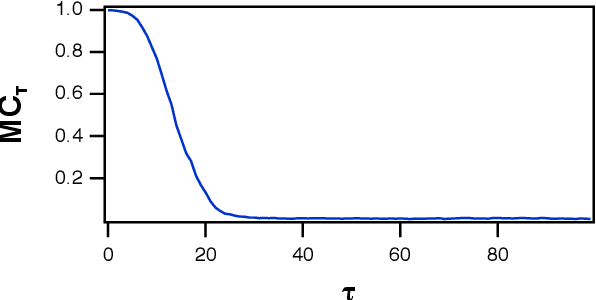
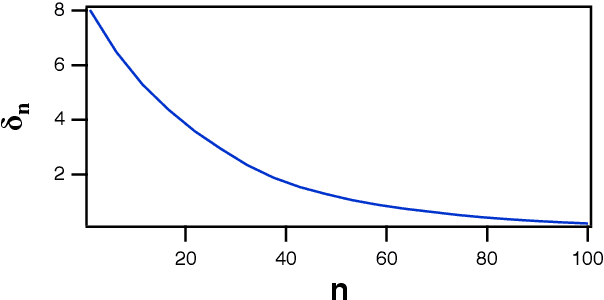
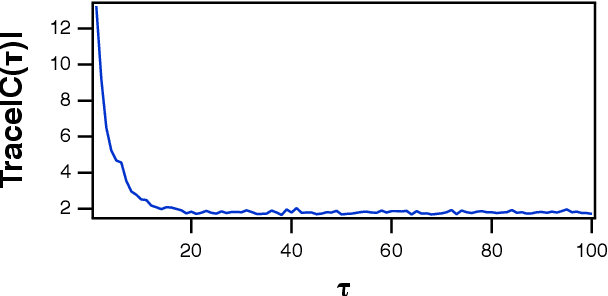
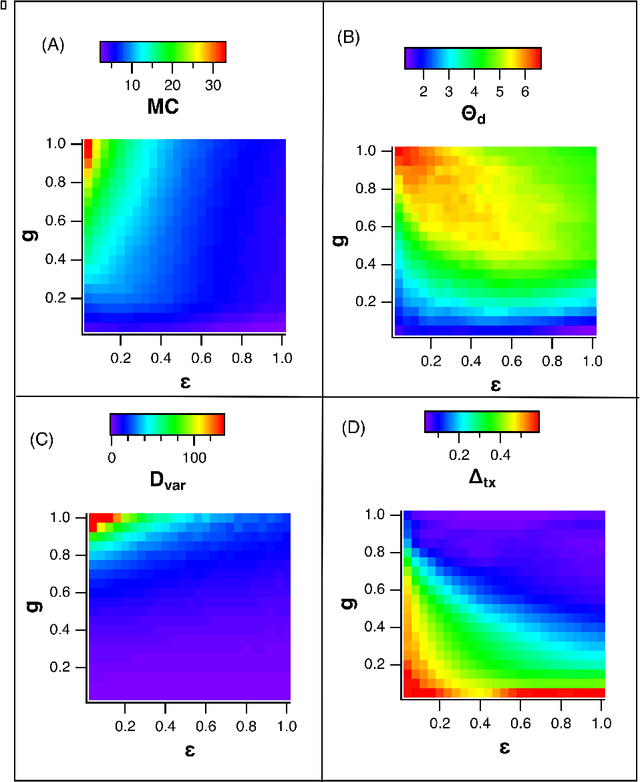
A reservoir computer is a way of using a high dimensional dynamical system for computation. One way to construct a reservoir computer is by connecting a set of nonlinear nodes into a network. Because the network creates feedback between nodes, the reservoir computer has memory. If the reservoir computer is to respond to an input signal in a consistent way (a necessary condition for computation), the memory must be fading; that is, the influence of the initial conditions fades over time. How long this memory lasts is important for determining how well the reservoir computer can solve a particular problem. In this paper I describe ways to vary the length of the fading memory in reservoir computers. Tuning the memory can be important to achieve optimal results in some problems; too much or too little memory degrades the accuracy of the computation.

Do Reservoir Computers Work Best at the Edge of Chaos?

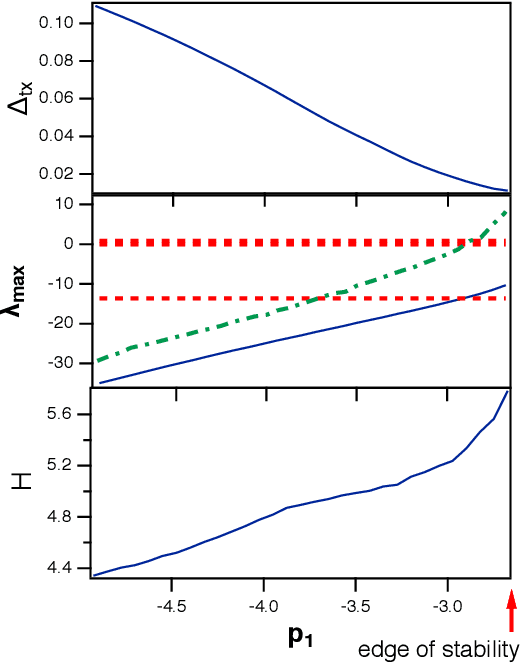
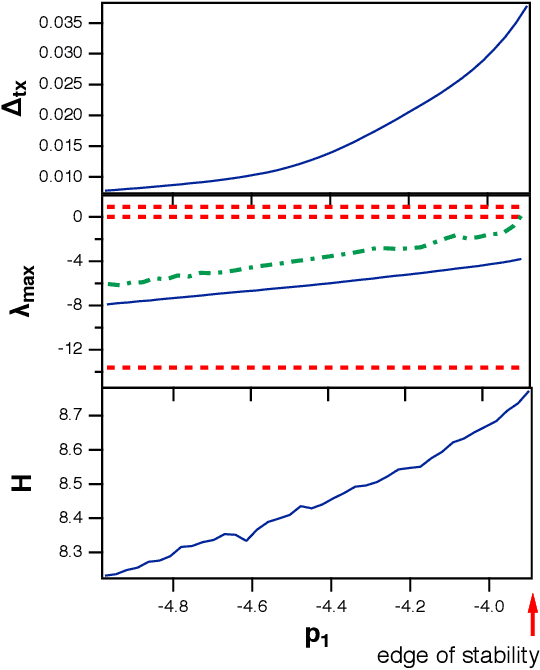
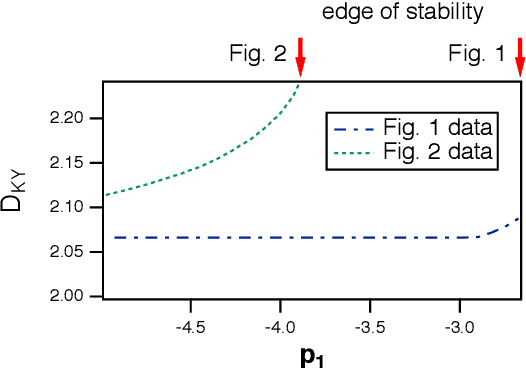
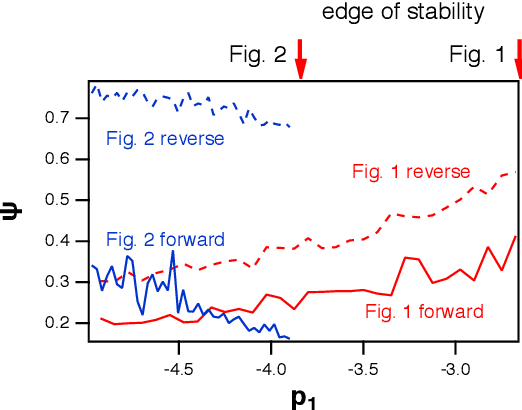
It has been demonstrated that cellular automata had the highest computational capacity at the edge of chaos, the parameter at which their behavior transitioned from ordered to chaotic. This same concept has been applied to reservoir computers; a number of researchers have stated that the highest computational capacity for a reservoir computer is at the edge of chaos, although others have suggested that this rule is not universally true. Because many reservoir computers do not show chaotic behavior but merely become unstable, it is felt that a more accurate term for this instability transition is the "edge of stability"Here I find two examples where the computational capacity of a reservoir computer decreases as the edge of stability is approached; in one case, because generalized synchronization breaks down, and in the other case because the reservoir computer is a poor match to the problem being solved. The edge of stability as an optimal operating point for a reservoir computer is not in general true, although it may be true in some cases.

Adding Filters to Improve Reservoir Computer Performance

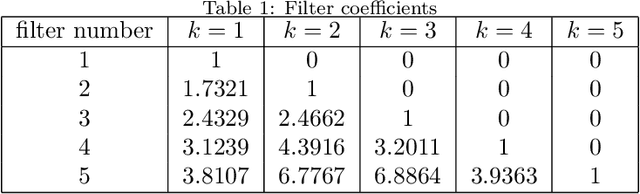
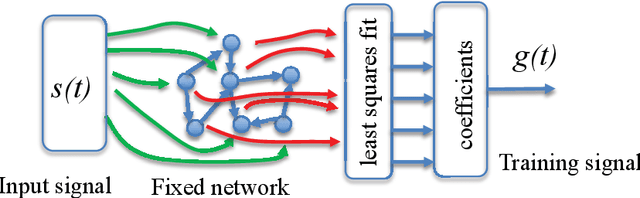
Reservoir computers are a type of neuromorphic computer that may be built a an analog system, potentially creating powerful computers that are small, light and consume little power. Typically a reservoir computer is build by connecting together a set of nonlinear nodes into a network; connecting the nonlinear nodes may be difficult or expensive, however. This work shows how a reservoir computer may be expanded by adding functions to its output. The particular functions described here are linear filters, but other functions are possible. The design and construction of linear filters is well known, and such filters may be easily implemented in hardware such as field programmable gate arrays (FPGA's). The effect of adding filters on the reservoir computer performance is simulated for a signal fitting problem, a prediction problem and a signal classification problem.

Dimension of Reservoir Computers

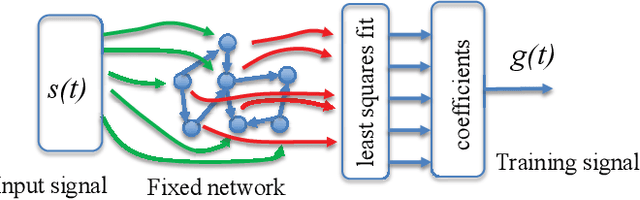
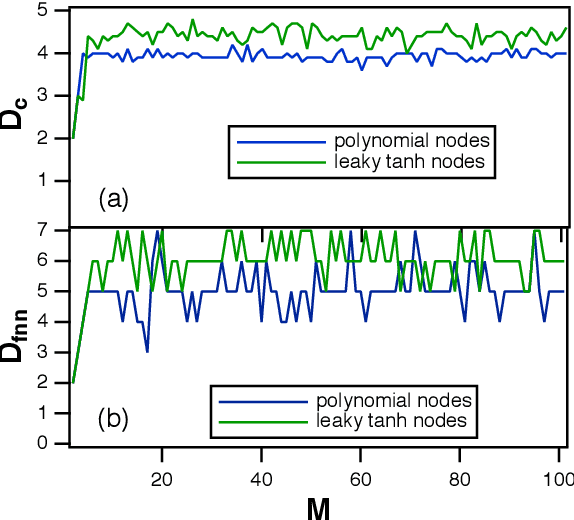
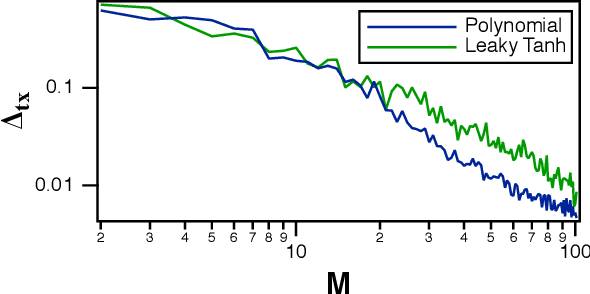
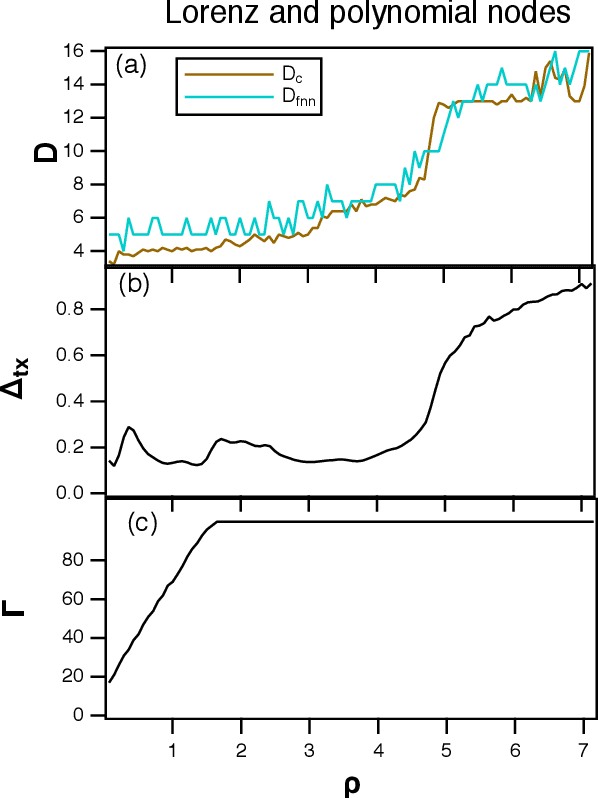
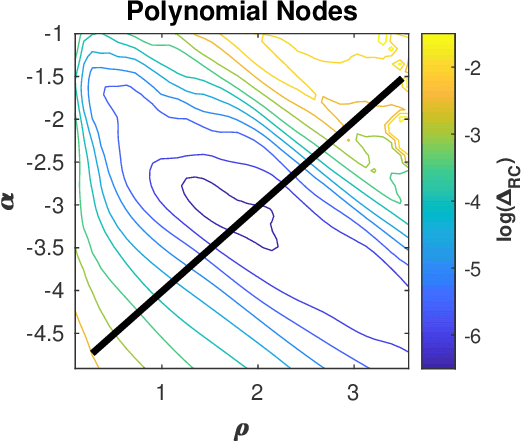
A reservoir computer is a complex dynamical system, often created by coupling nonlinear nodes in a network. The nodes are all driven by a common driving signal. In this work, three dimension estimation methods, false nearest neighbor, covariance and Kaplan-Yorke dimensions, are used to estimate the dimension of the reservoir dynamical system. It is shown that the signals in the reservoir system exist on a relatively low dimensional surface. Changing the spectral radius of the reservoir network can increase the fractal dimension of the reservoir signals, leading to an increase in testing error.

Mutual Information and the Edge of Chaos in Reservoir Computers

A reservoir computer is a dynamical system that may be used to perform computations. A reservoir computer usually consists of a set of nonlinear nodes coupled together in a network so that there are feedback paths. Training the reservoir computer consists of inputing a signal of interest and fitting the time series signals of the reservoir computer nodes to a training signal that is related to the input signal. It is believed that dynamical systems function most efficiently as computers at the "edge of chaos", the point at which the largest Lyapunov exponent of the dynamical system transitions from negative to positive. In this work I simulate several different reservoir computers and ask if the best performance really does come at this edge of chaos. I find that while it is possible to get optimum performance at the edge of chaos, there may also be parameter values where the edge of chaos regime produces poor performance. This ambiguous parameter dependance has implications for building reservoir computers from analog physical systems, where the parameter range is restricted.