Do Reservoir Computers Work Best at the Edge of Chaos?
Paper and Code
Dec 02, 2020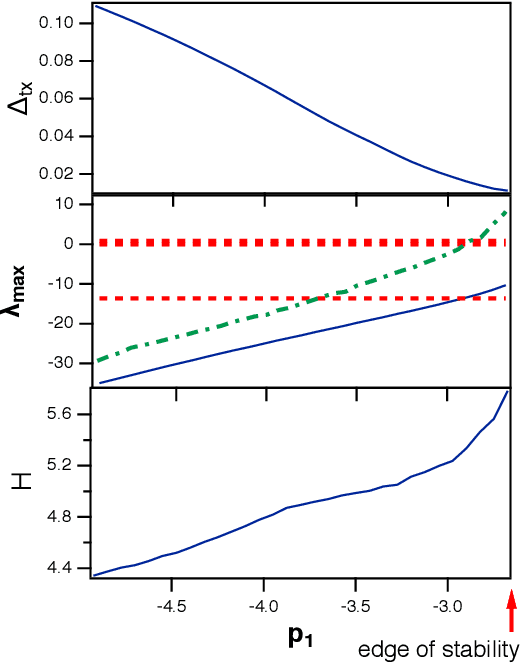
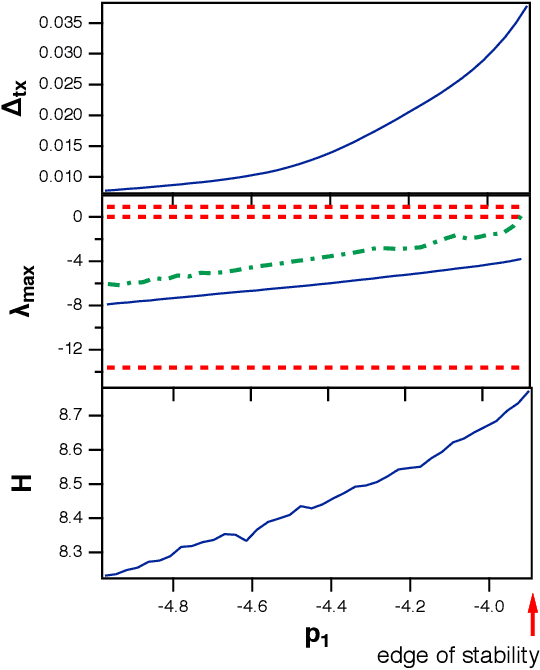
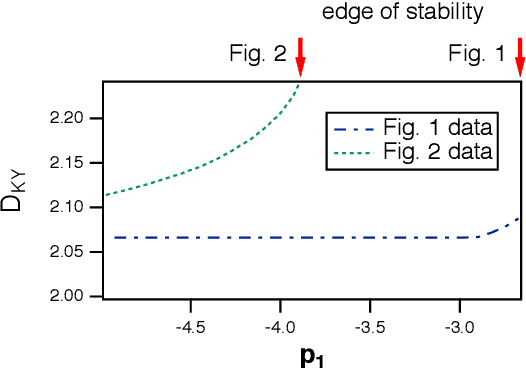
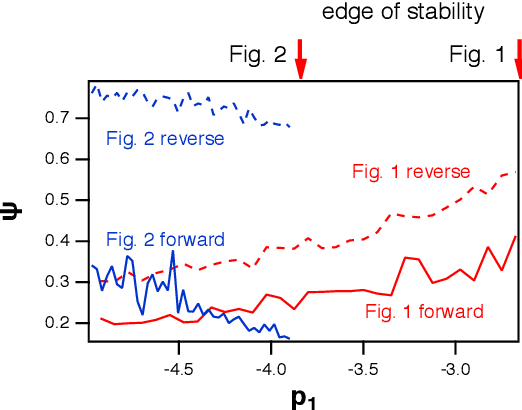
It has been demonstrated that cellular automata had the highest computational capacity at the edge of chaos, the parameter at which their behavior transitioned from ordered to chaotic. This same concept has been applied to reservoir computers; a number of researchers have stated that the highest computational capacity for a reservoir computer is at the edge of chaos, although others have suggested that this rule is not universally true. Because many reservoir computers do not show chaotic behavior but merely become unstable, it is felt that a more accurate term for this instability transition is the "edge of stability"Here I find two examples where the computational capacity of a reservoir computer decreases as the edge of stability is approached; in one case, because generalized synchronization breaks down, and in the other case because the reservoir computer is a poor match to the problem being solved. The edge of stability as an optimal operating point for a reservoir computer is not in general true, although it may be true in some cases.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge