Mutual Information and the Edge of Chaos in Reservoir Computers
Paper and Code
Jul 19, 2019
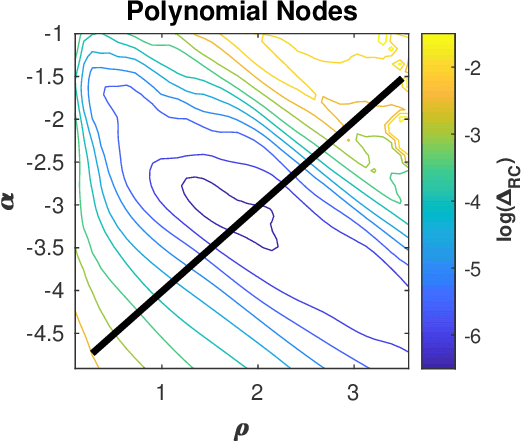


A reservoir computer is a dynamical system that may be used to perform computations. A reservoir computer usually consists of a set of nonlinear nodes coupled together in a network so that there are feedback paths. Training the reservoir computer consists of inputing a signal of interest and fitting the time series signals of the reservoir computer nodes to a training signal that is related to the input signal. It is believed that dynamical systems function most efficiently as computers at the "edge of chaos", the point at which the largest Lyapunov exponent of the dynamical system transitions from negative to positive. In this work I simulate several different reservoir computers and ask if the best performance really does come at this edge of chaos. I find that while it is possible to get optimum performance at the edge of chaos, there may also be parameter values where the edge of chaos regime produces poor performance. This ambiguous parameter dependance has implications for building reservoir computers from analog physical systems, where the parameter range is restricted.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge