RCUKF: Data-Driven Modeling Meets Bayesian Estimation

Accurate modeling is crucial in many engineering and scientific applications, yet obtaining a reliable process model for complex systems is often challenging. To address this challenge, we propose a novel framework, reservoir computing with unscented Kalman filtering (RCUKF), which integrates data-driven modeling via reservoir computing (RC) with Bayesian estimation through the unscented Kalman filter (UKF). The RC component learns the nonlinear system dynamics directly from data, serving as a surrogate process model in the UKF prediction step to generate state estimates in high-dimensional or chaotic regimes where nominal mathematical models may fail. Meanwhile, the UKF measurement update integrates real-time sensor data to correct potential drift in the data-driven model. We demonstrate RCUKF effectiveness on well-known benchmark problems and a real-time vehicle trajectory estimation task in a high-fidelity simulation environment.

Reservoir Computing with Noise

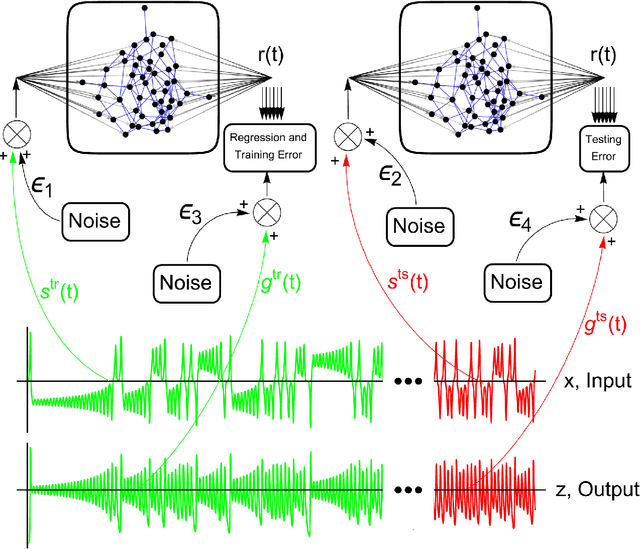
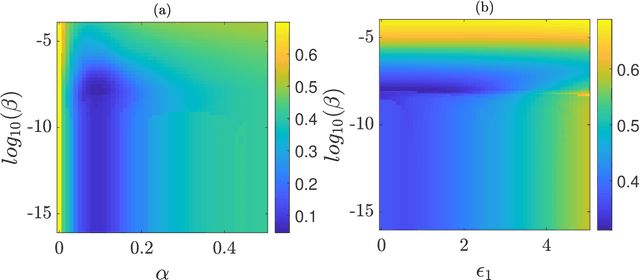
This paper investigates in detail the effects of noise on the performance of reservoir computing. We focus on an application in which reservoir computers are used to learn the relationship between different state variables of a chaotic system. We recognize that noise can affect differently the training and testing phases. We find that the best performance of the reservoir is achieved when the strength of the noise that affects the input signal in the training phase equals the strength of the noise that affects the input signal in the testing phase. For all the cases we examined, we found that a good remedy to noise is to low-pass filter the input and the training/testing signals; this typically preserves the performance of the reservoir, while reducing the undesired effects of noise.

Optimizing time-shifts for reservoir computing using a rank-revealing QR algorithm

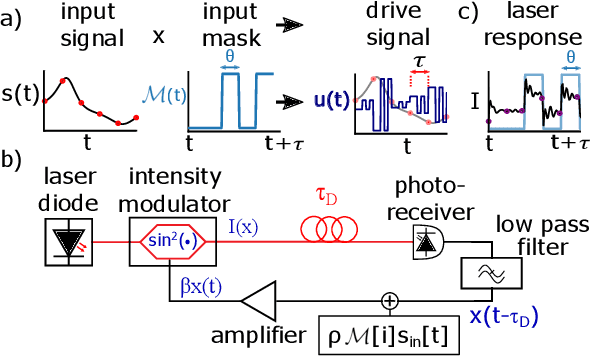
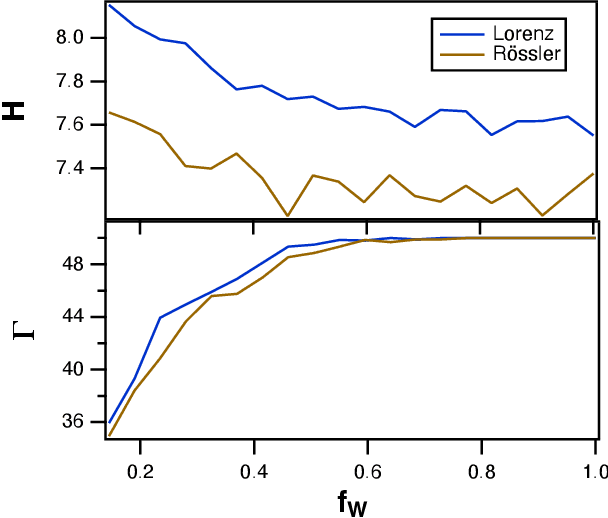
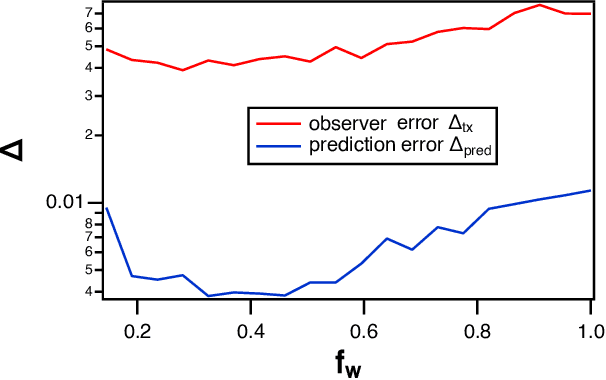
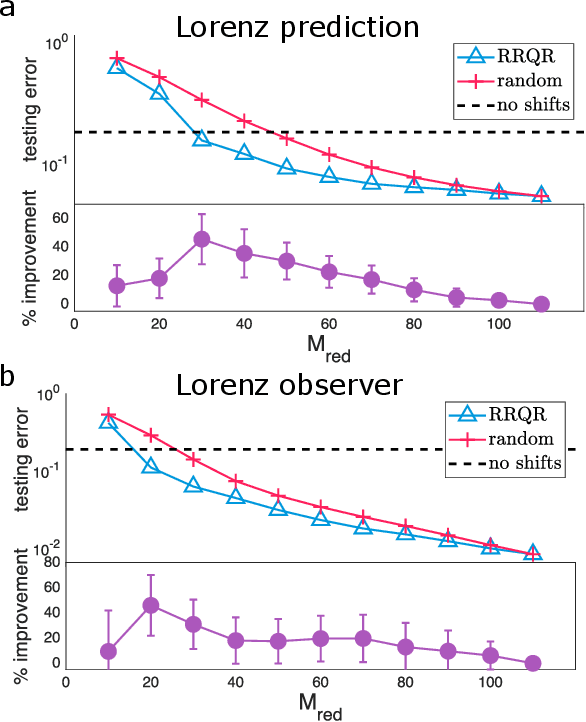
Reservoir computing is a recurrent neural network paradigm in which only the output layer is trained. Recently, it was demonstrated that adding time-shifts to the signals generated by a reservoir can provide large improvements in performance accuracy. In this work, we present a technique to choose the optimal time shifts. Our technique maximizes the rank of the reservoir matrix using a rank-revealing QR algorithm and is not task dependent. Further, our technique does not require a model of the system, and therefore is directly applicable to analog hardware reservoir computers. We demonstrate our time-shift optimization technique on two types of reservoir computer: one based on an opto-electronic oscillator and the traditional recurrent network with a $tanh$ activation function. We find that our technique provides improved accuracy over random time-shift selection in essentially all cases.

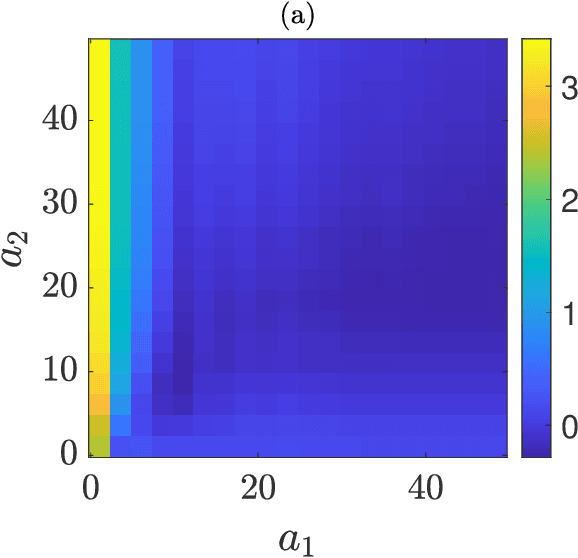
Reservoir Computers Modal Decomposition and Optimization

The topology of a network associated with a reservoir computer is often taken so that the connectivity and the weights are chosen randomly. Optimization is hardly considered as the parameter space is typically too large. Here we investigate this problem for a class of reservoir computers for which we obtain a decomposition of the reservoir dynamics into modes, which can be computed independently of one another. Each mode depends on an eigenvalue of the network adjacency matrix. We then take a parametric approach in which the eigenvalues are parameters that can be appropriately designed and optimized. In addition, we introduce the application of a time shift to each individual mode. We show that manipulations of the individual modes, either in terms of the eigenvalues or the time shifts, can lead to dramatic reductions in the training error.

Decentralized identification and control of networks of coupled mobile platforms through adaptive synchronization of chaos

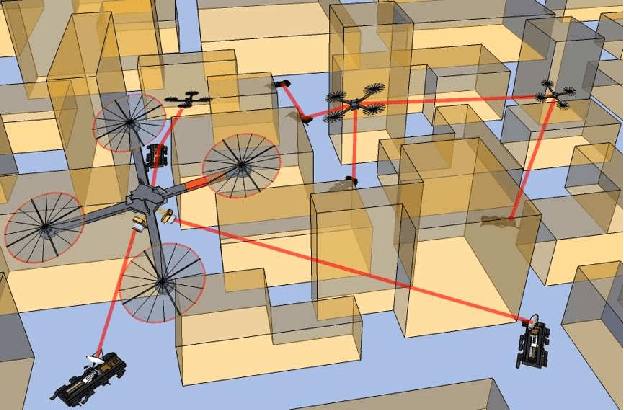
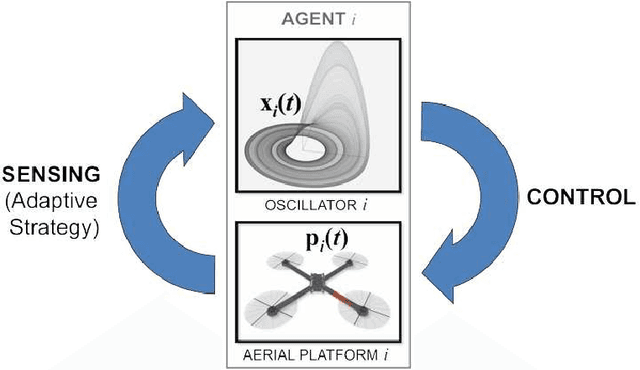
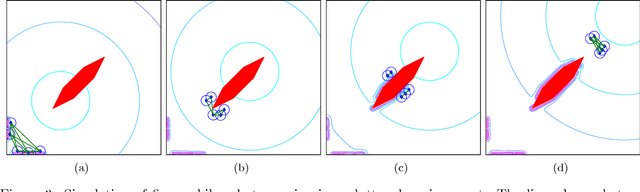
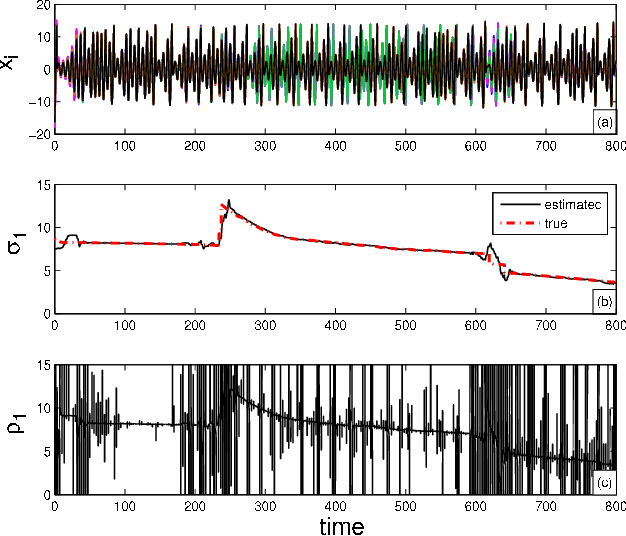
In this paper we propose an application of adaptive synchronization of chaos to detect changes in the topology of a mobile robotic network. We assume that the network may evolve in time due to the relative motion of the mobile robots and due to unknown environmental conditions, such as the presence of obstacles in the environment. We consider that each robotic agent is equipped with a chaotic oscillator whose state is propagated to the other robots through wireless communication, with the goal of synchronizing the oscillators. We introduce an adaptive strategy that each agent independently implements to: (i) estimate the net coupling of all the oscillators in its neighborhood and (ii) synchronize the state of the oscillators onto the same time evolution. We show that by using this strategy, synchronization can be attained and changes in the network topology can be detected. We go one step forward and consider the possibility of using this information to control the mobile network. We show the potential applicability of our technique to the problem of maintaining a formation between a set of mobile platforms, which operate in an inhomogeneous and uncertain environment. We discuss the importance of using chaotic oscillators and validate our methodology by numerical simulations.