Chad Nathe
Reservoir Computing with Noise
Feb 28, 2023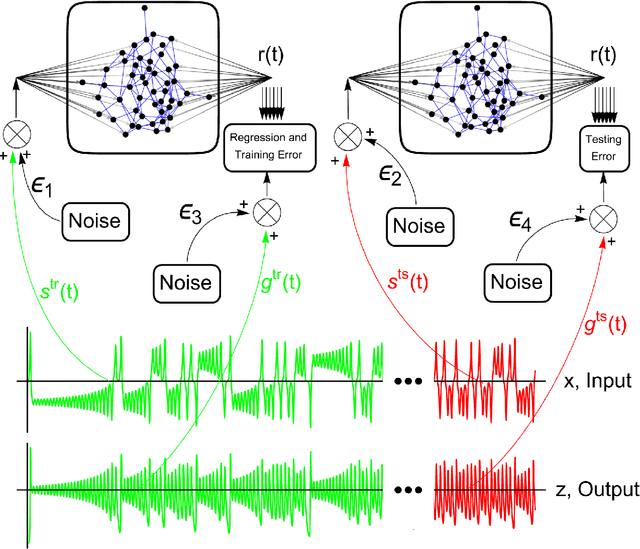
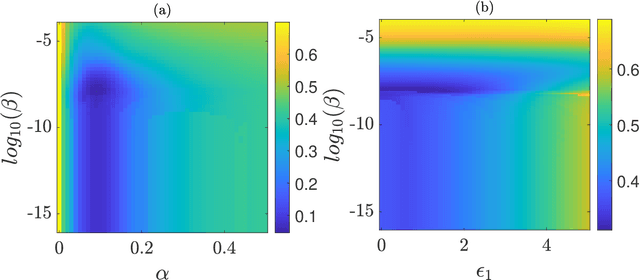

Abstract:This paper investigates in detail the effects of noise on the performance of reservoir computing. We focus on an application in which reservoir computers are used to learn the relationship between different state variables of a chaotic system. We recognize that noise can affect differently the training and testing phases. We find that the best performance of the reservoir is achieved when the strength of the noise that affects the input signal in the training phase equals the strength of the noise that affects the input signal in the testing phase. For all the cases we examined, we found that a good remedy to noise is to low-pass filter the input and the training/testing signals; this typically preserves the performance of the reservoir, while reducing the undesired effects of noise.
Reservoir Computers Modal Decomposition and Optimization
Jan 13, 2021



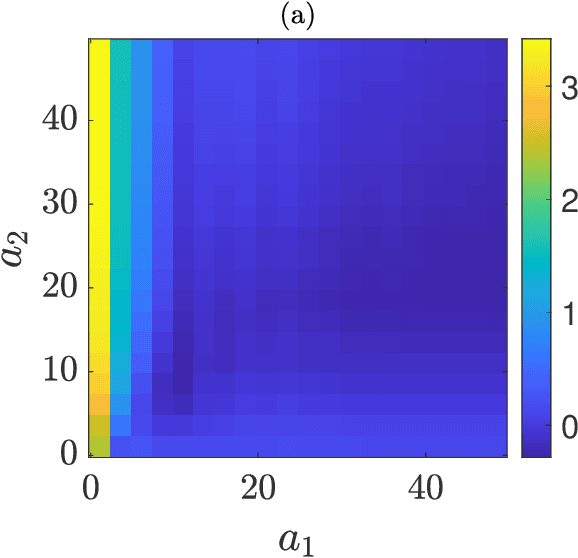
Abstract:The topology of a network associated with a reservoir computer is often taken so that the connectivity and the weights are chosen randomly. Optimization is hardly considered as the parameter space is typically too large. Here we investigate this problem for a class of reservoir computers for which we obtain a decomposition of the reservoir dynamics into modes, which can be computed independently of one another. Each mode depends on an eigenvalue of the network adjacency matrix. We then take a parametric approach in which the eigenvalues are parameters that can be appropriately designed and optimized. In addition, we introduce the application of a time shift to each individual mode. We show that manipulations of the individual modes, either in terms of the eigenvalues or the time shifts, can lead to dramatic reductions in the training error.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge