Reservoir Computing with Noise
Paper and Code
Feb 28, 2023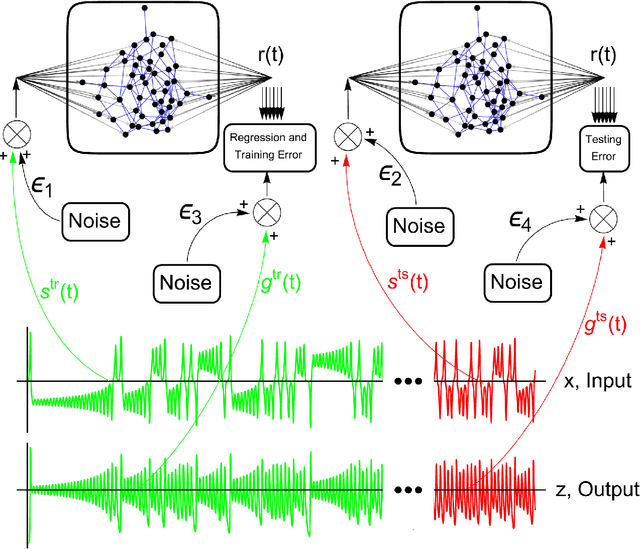
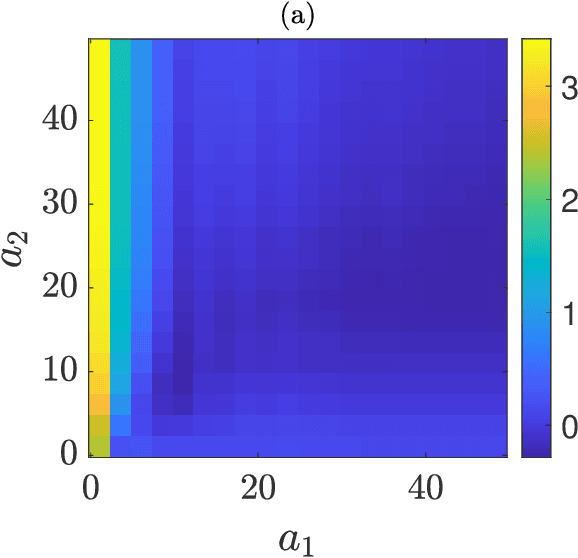
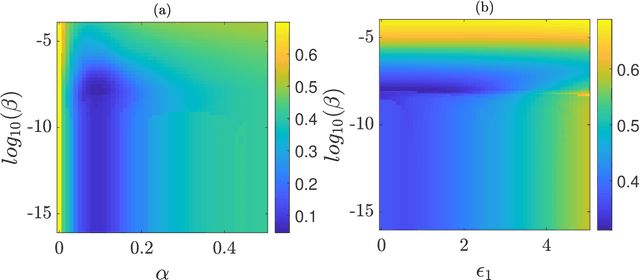

This paper investigates in detail the effects of noise on the performance of reservoir computing. We focus on an application in which reservoir computers are used to learn the relationship between different state variables of a chaotic system. We recognize that noise can affect differently the training and testing phases. We find that the best performance of the reservoir is achieved when the strength of the noise that affects the input signal in the training phase equals the strength of the noise that affects the input signal in the testing phase. For all the cases we examined, we found that a good remedy to noise is to low-pass filter the input and the training/testing signals; this typically preserves the performance of the reservoir, while reducing the undesired effects of noise.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge