Dimension of Reservoir Computers
Paper and Code
Dec 10, 2019
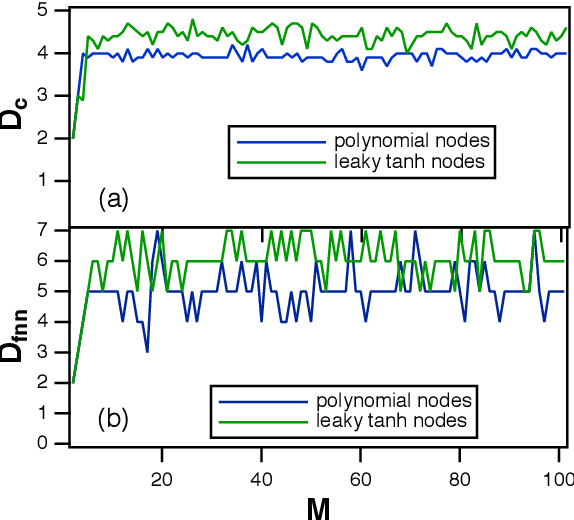
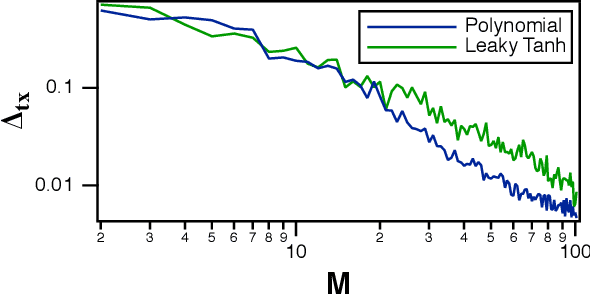
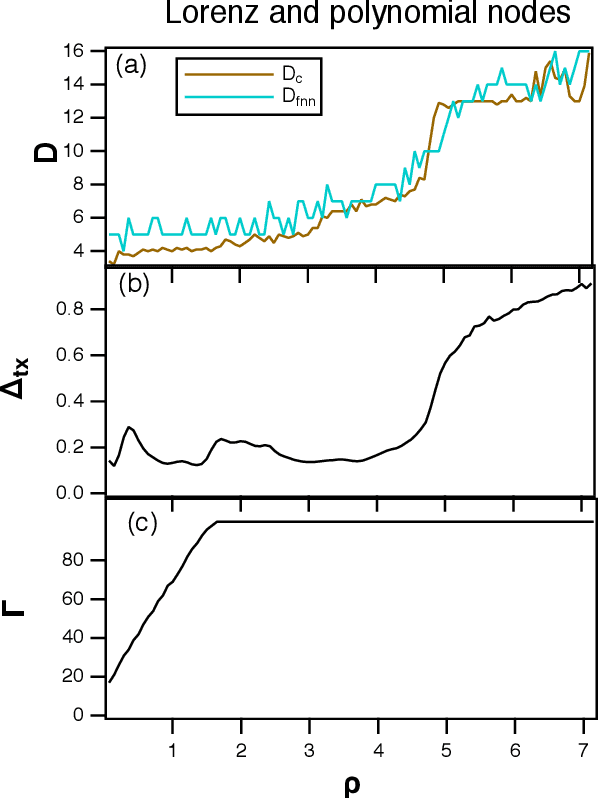
A reservoir computer is a complex dynamical system, often created by coupling nonlinear nodes in a network. The nodes are all driven by a common driving signal. In this work, three dimension estimation methods, false nearest neighbor, covariance and Kaplan-Yorke dimensions, are used to estimate the dimension of the reservoir dynamical system. It is shown that the signals in the reservoir system exist on a relatively low dimensional surface. Changing the spectral radius of the reservoir network can increase the fractal dimension of the reservoir signals, leading to an increase in testing error.
* submitted to Chaos
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge