A theoretical framework for reservoir computing on networks of organic electrochemical transistors
Paper and Code
Aug 17, 2024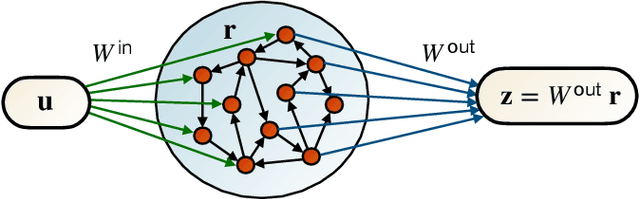
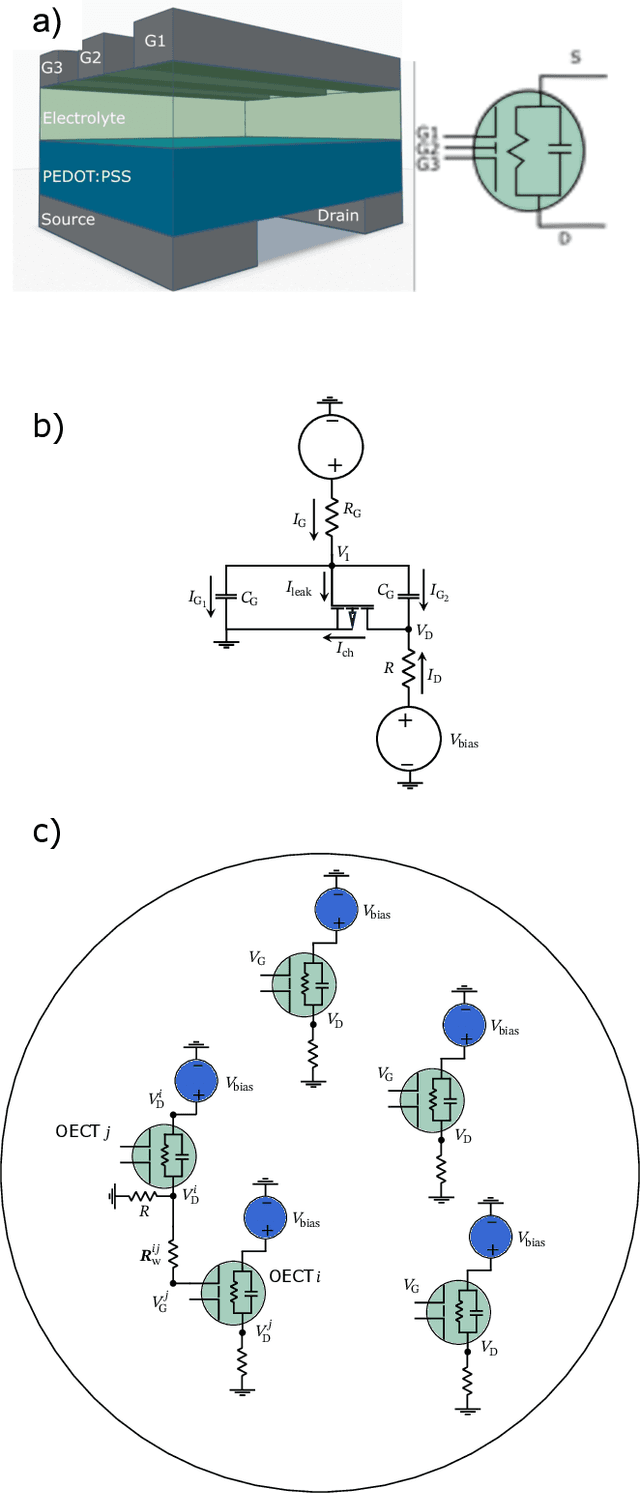
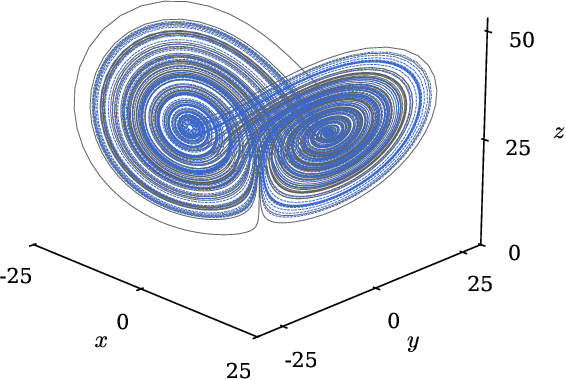
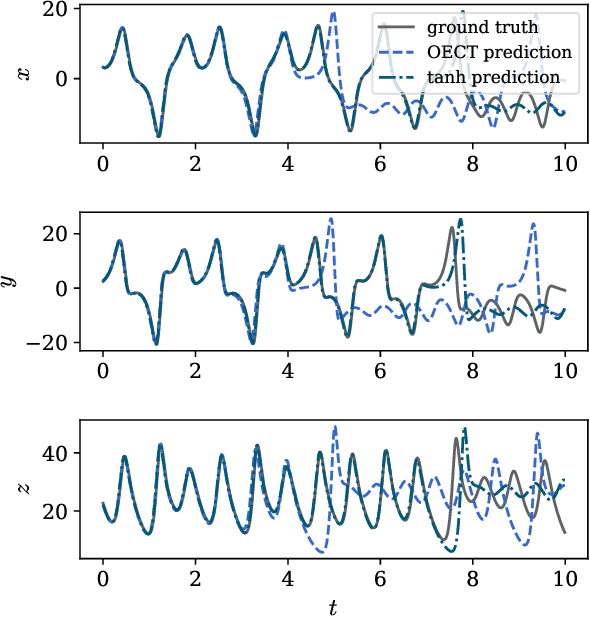
Efficient and accurate prediction of physical systems is important even when the rules of those systems cannot be easily learned. Reservoir computing, a type of recurrent neural network with fixed nonlinear units, is one such prediction method and is valued for its ease of training. Organic electrochemical transistors (OECTs) are physical devices with nonlinear transient properties that can be used as the nonlinear units of a reservoir computer. We present a theoretical framework for simulating reservoir computers using OECTs as the non-linear units as a test bed for designing physical reservoir computers. We present a proof of concept demonstrating that such an implementation can accurately predict the Lorenz attractor with comparable performance to standard reservoir computer implementations. We explore the effect of operating parameters and find that the prediction performance strongly depends on the pinch-off voltage of the OECTs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge