Alice Patania
Topological Learning for Motion Data via Mixed Coordinates
Oct 30, 2023



Abstract:Topology can extract the structural information in a dataset efficiently. In this paper, we attempt to incorporate topological information into a multiple output Gaussian process model for transfer learning purposes. To achieve this goal, we extend the framework of circular coordinates into a novel framework of mixed valued coordinates to take linear trends in the time series into consideration. One of the major challenges to learn from multiple time series effectively via a multiple output Gaussian process model is constructing a functional kernel. We propose to use topologically induced clustering to construct a cluster based kernel in a multiple output Gaussian process model. This kernel not only incorporates the topological structural information, but also allows us to put forward a unified framework using topological information in time and motion series.
* 7 pages, 4 figures
Exact and rapid linear clustering of networks with dynamic programming
Jan 25, 2023Abstract:We study the problem of clustering networks whose nodes have imputed or physical positions in a single dimension, such as prestige hierarchies or the similarity dimension of hyperbolic embeddings. Existing algorithms, such as the critical gap method and other greedy strategies, only offer approximate solutions. Here, we introduce a dynamic programming approach that returns provably optimal solutions in polynomial time -- O(n^2) steps -- for a broad class of clustering objectives. We demonstrate the algorithm through applications to synthetic and empirical networks, and show that it outperforms existing heuristics by a significant margin, with a similar execution time.
Generalized Penalty for Circular Coordinate Representation
Jun 03, 2020
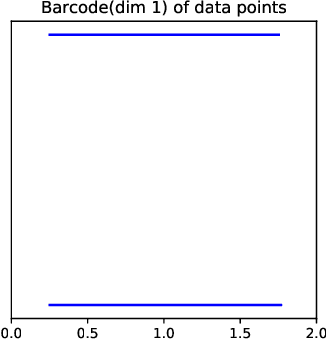
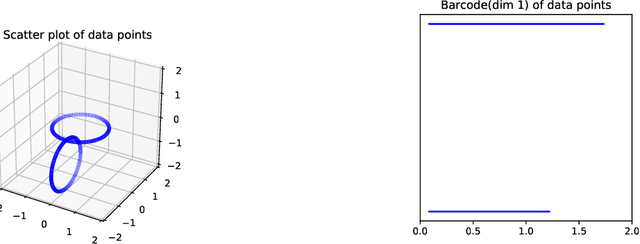
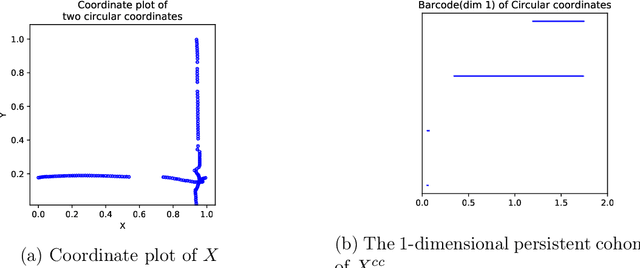
Abstract:Topological Data Analysis (TDA) provides novel approaches that allow us to analyze the geometrical shapes and topological structures of a dataset. As one important application, TDA can be used for data visualization and dimension reduction. We follow the framework of circular coordinate representation, which allows us to perform dimension reduction and visualization for high-dimensional datasets on a torus using persistent cohomology. In this paper, we propose a method to adapt the circular coordinate framework to take into account sparsity in high-dimensional applications. We use a generalized penalty function instead of an $L_{2}$ penalty in the traditional circular coordinate algorithm. We provide simulation experiments and real data analysis to support our claim that circular coordinates with generalized penalty will accommodate the sparsity in high-dimensional datasets under different sampling schemes while preserving the topological structures.
Complex Politics: A Quantitative Semantic and Topological Analysis of UK House of Commons Debates
Oct 13, 2015


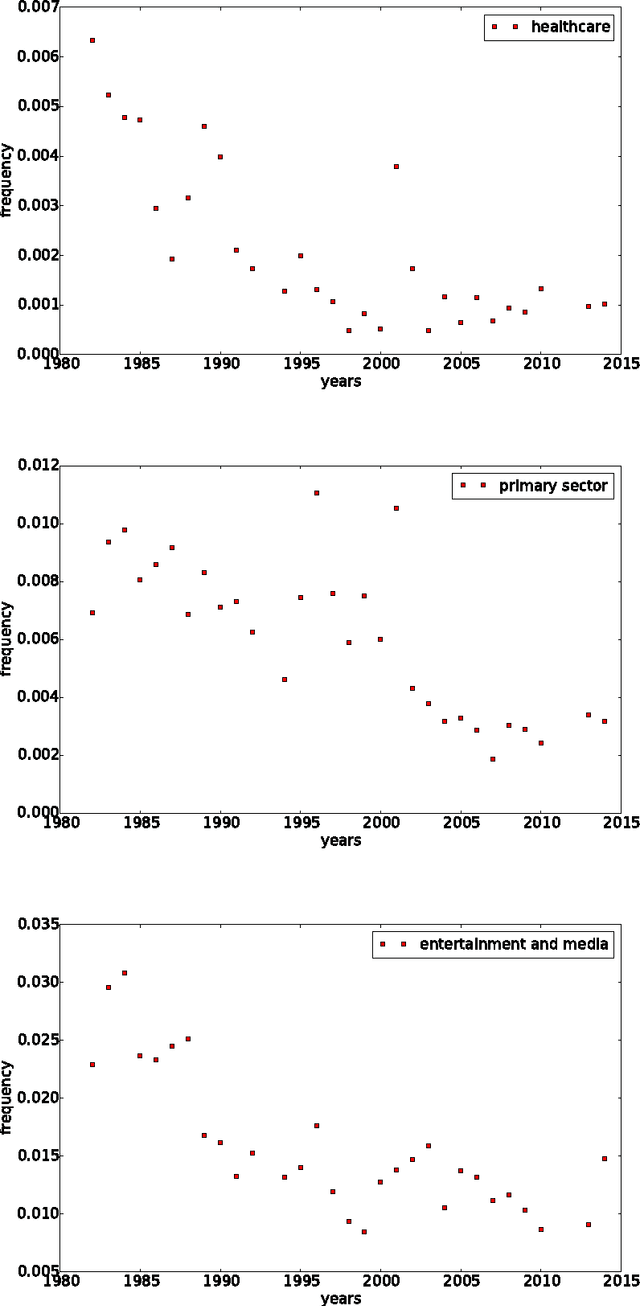
Abstract:This study is a first, exploratory attempt to use quantitative semantics techniques and topological analysis to analyze systemic patterns arising in a complex political system. In particular, we use a rich data set covering all speeches and debates in the UK House of Commons between 1975 and 2014. By the use of dynamic topic modeling (DTM) and topological data analysis (TDA) we show that both members and parties feature specific roles within the system, consistent over time, and extract global patterns indicating levels of political cohesion. Our results provide a wide array of novel hypotheses about the complex dynamics of political systems, with valuable policy applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge