Principled inference of hyperedges and overlapping communities in hypergraphs

Hypergraphs, encoding structured interactions among any number of system units, have recently proven a successful tool to describe many real-world biological and social networks. Here we propose a framework based on statistical inference to characterize the structural organization of hypergraphs. The method allows to infer missing hyperedges of any size in a principled way, and to jointly detect overlapping communities in presence of higher-order interactions. Furthermore, our model has an efficient numerical implementation, and it runs faster than dyadic algorithms on pairwise records projected from higher-order data. We apply our method to a variety of real-world systems, showing strong performance in hyperedge prediction tasks, detecting communities well aligned with the information carried by interactions, and robustness against addition of noisy hyperedges. Our approach illustrates the fundamental advantages of a hypergraph probabilistic model when modeling relational systems with higher-order interactions.

Complex Politics: A Quantitative Semantic and Topological Analysis of UK House of Commons Debates

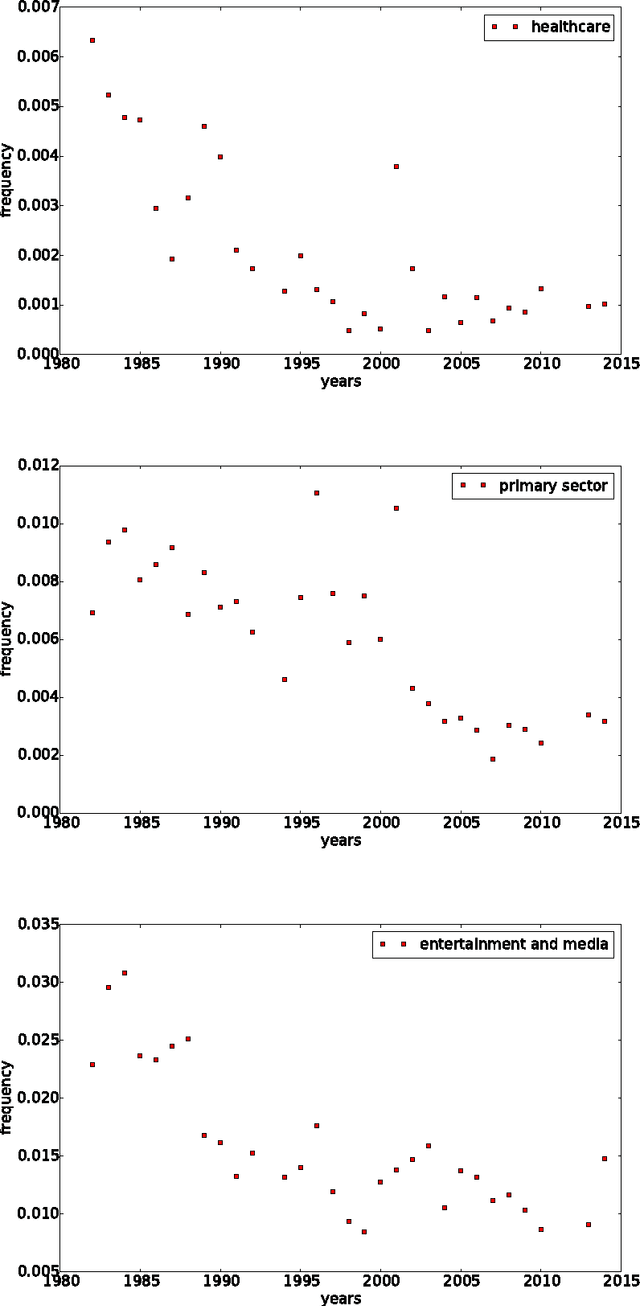
This study is a first, exploratory attempt to use quantitative semantics techniques and topological analysis to analyze systemic patterns arising in a complex political system. In particular, we use a rich data set covering all speeches and debates in the UK House of Commons between 1975 and 2014. By the use of dynamic topic modeling (DTM) and topological data analysis (TDA) we show that both members and parties feature specific roles within the system, consistent over time, and extract global patterns indicating levels of political cohesion. Our results provide a wide array of novel hypotheses about the complex dynamics of political systems, with valuable policy applications.