Known by the company we keep: `Triadic influence' as a proxy for compatibility in social relationships

Networks of social interactions are the substrate upon which civilizations are built. Often, we create new bonds with people that we like or feel that our relationships are damaged through the intervention of third parties. Despite their importance and the huge impact that these processes have in our lives, quantitative scientific understanding of them is still in its infancy, mainly due to the difficulty of collecting large datasets of social networks including individual attributes. In this work, we present a thorough study of real social networks of 13 schools, with more than 3,000 students and 60,000 declared positive and negative relations, including tests for personal traits of all the students. We introduce a metric -- the `triadic influence' -- that measures the influence of nearest-neighbors in the relationships of their contacts. We use neural networks to predict the relationships and to extract the probability that two students are friends or enemies depending on their personal attributes or the triadic influence. We alternatively use a high-dimensional embedding of the network structure to also predict the relationships. Remarkably, the triadic influence (a simple one-dimensional metric) achieves the highest accuracy at predicting the relationship between two students. We postulate that the probabilities extracted from the neural networks -- functions of the triadic influence and the personalities of the students -- control the evolution of real social networks, opening a new avenue for the quantitative study of these systems.

Hierarchical clustering of bipartite data sets based on the statistical significance of coincidences

When a set 'entities' are related by the 'features' they share they are amenable to a bipartite network representation. Plant-pollinator ecological communities, co-authorship of scientific papers, customers and purchases, or answers in a poll, are but a few examples. Analysing clustering of such entities in the network is a useful tool with applications in many fields, like internet technology, recommender systems, or detection of diseases. The algorithms most widely applied to find clusters in bipartite networks are variants of modularity optimisation. Here we provide an hierarchical clustering algorithm based on a dissimilarity between entities that quantifies the probability that the features shared by two entities is due to mere chance. The algorithm performance is $O(n^{2})$ when applied to a set of $n$ entities, and its outcome is a dendrogram exhibiting the connections of those entities. Through the introduction of a 'susceptibility' measure we can provide an 'optimal' choice for the clustering as well as quantify its quality. The dendrogram reveals further useful structural information though -- like the existence of sub-clusters within clusters. We illustrate the algorithm by applying it first to a set of synthetic networks, and then to a selection of examples. We also illustrate how to transform our algorithm into a valid alternative for uni-modal networks as well, and show that it performs at least as well as the standard, modularity-based algorithms -- with a higher numerical performance. We provide an implementation of the algorithm in Python freely accessible from GitHub.

Complex Politics: A Quantitative Semantic and Topological Analysis of UK House of Commons Debates

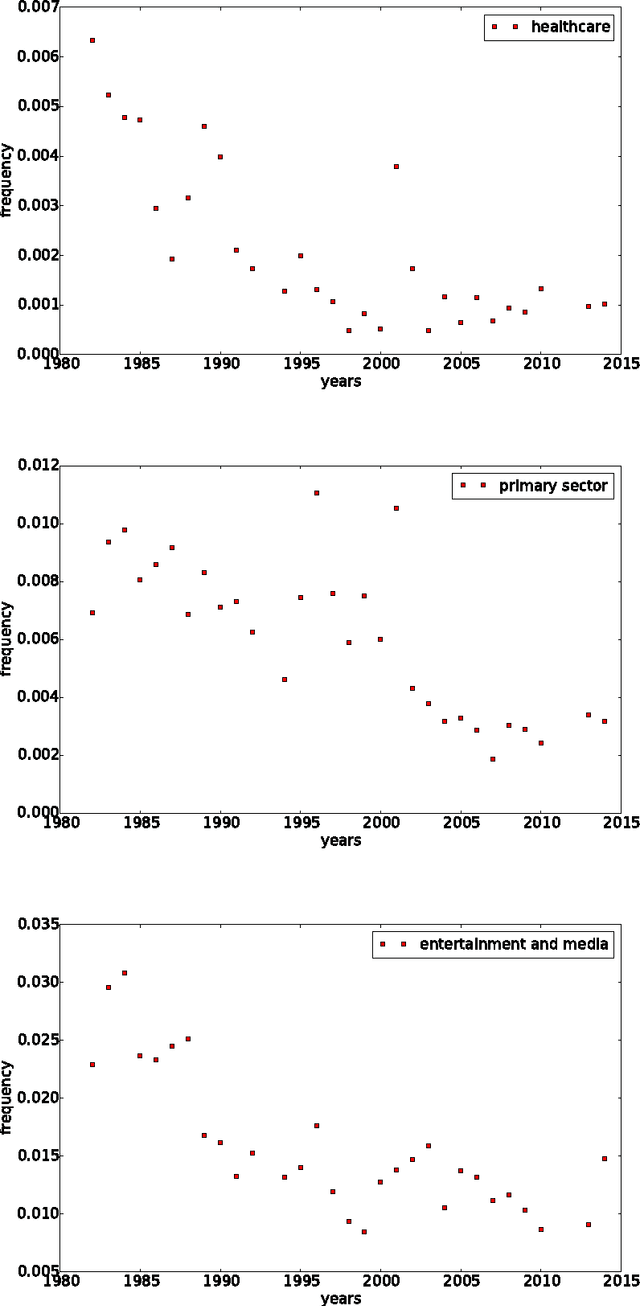
This study is a first, exploratory attempt to use quantitative semantics techniques and topological analysis to analyze systemic patterns arising in a complex political system. In particular, we use a rich data set covering all speeches and debates in the UK House of Commons between 1975 and 2014. By the use of dynamic topic modeling (DTM) and topological data analysis (TDA) we show that both members and parties feature specific roles within the system, consistent over time, and extract global patterns indicating levels of political cohesion. Our results provide a wide array of novel hypotheses about the complex dynamics of political systems, with valuable policy applications.