EnQode: Fast Amplitude Embedding for Quantum Machine Learning Using Classical Data

Amplitude embedding (AE) is essential in quantum machine learning (QML) for encoding classical data onto quantum circuits. However, conventional AE methods suffer from deep, variable-length circuits that introduce high output error due to extensive gate usage and variable error rates across samples, resulting in noise-driven inconsistencies that degrade model accuracy. We introduce EnQode, a fast AE technique based on symbolic representation that addresses these limitations by clustering dataset samples and solving for cluster mean states through a low-depth, machine-specific ansatz. Optimized to reduce physical gates and SWAP operations, EnQode ensures all samples face consistent, low noise levels by standardizing circuit depth and composition. With over 90% fidelity in data mapping, EnQode enables robust, high-performance QML on noisy intermediate-scale quantum (NISQ) devices. Our open-source solution provides a scalable and efficient alternative for integrating classical data with quantum models.

Kernel-based estimators for functional causal effects

We propose causal effect estimators based on empirical Fr\'{e}chet means and operator-valued kernels, tailored to functional data spaces. These methods address the challenges of high-dimensionality, sequential ordering, and model complexity while preserving robustness to treatment misspecification. Using structural assumptions, we obtain compact representations of potential outcomes, enabling scalable estimation of causal effects over time and across covariates. We provide both theoretical, regarding the consistency of functional causal effects, as well as empirical comparison of a range of proposed causal effect estimators. Applications to binary treatment settings with functional outcomes illustrate the framework's utility in biomedical monitoring, where outcomes exhibit complex temporal dynamics. Our estimators accommodate scenarios with registered covariates and outcomes, aligning them to the Fr\'{e}chet means, as well as cases requiring higher-order representations to capture intricate covariate-outcome interactions. These advancements extend causal inference to dynamic and non-linear domains, offering new tools for understanding complex treatment effects in functional data settings.

Asymptotic Optimism of Random-Design Linear and Kernel Regression Models

We derived the closed-form asymptotic optimism of linear regression models under random designs, and generalizes it to kernel ridge regression. Using scaled asymptotic optimism as a generic predictive model complexity measure, we studied the fundamental different behaviors of linear regression model, tangent kernel (NTK) regression model and three-layer fully connected neural networks (NN). Our contribution is two-fold: we provided theoretical ground for using scaled optimism as a model predictive complexity measure; and we show empirically that NN with ReLUs behaves differently from kernel models under this measure. With resampling techniques, we can also compute the optimism for regression models with real data.

Compactly-supported nonstationary kernels for computing exact Gaussian processes on big data

The Gaussian process (GP) is a widely used probabilistic machine learning method for stochastic function approximation, stochastic modeling, and analyzing real-world measurements of nonlinear processes. Unlike many other machine learning methods, GPs include an implicit characterization of uncertainty, making them extremely useful across many areas of science, technology, and engineering. Traditional implementations of GPs involve stationary kernels (also termed covariance functions) that limit their flexibility and exact methods for inference that prevent application to data sets with more than about ten thousand points. Modern approaches to address stationarity assumptions generally fail to accommodate large data sets, while all attempts to address scalability focus on approximating the Gaussian likelihood, which can involve subjectivity and lead to inaccuracies. In this work, we explicitly derive an alternative kernel that can discover and encode both sparsity and nonstationarity. We embed the kernel within a fully Bayesian GP model and leverage high-performance computing resources to enable the analysis of massive data sets. We demonstrate the favorable performance of our novel kernel relative to existing exact and approximate GP methods across a variety of synthetic data examples. Furthermore, we conduct space-time prediction based on more than one million measurements of daily maximum temperature and verify that our results outperform state-of-the-art methods in the Earth sciences. More broadly, having access to exact GPs that use ultra-scalable, sparsity-discovering, nonstationary kernels allows GP methods to truly compete with a wide variety of machine learning methods.

Ranking Perspective for Tree-based Methods with Applications to Symbolic Feature Selection

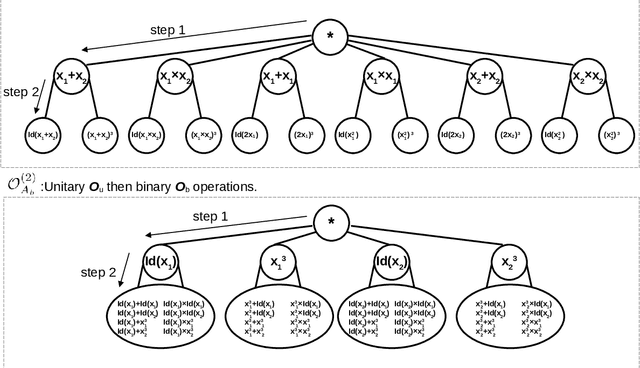
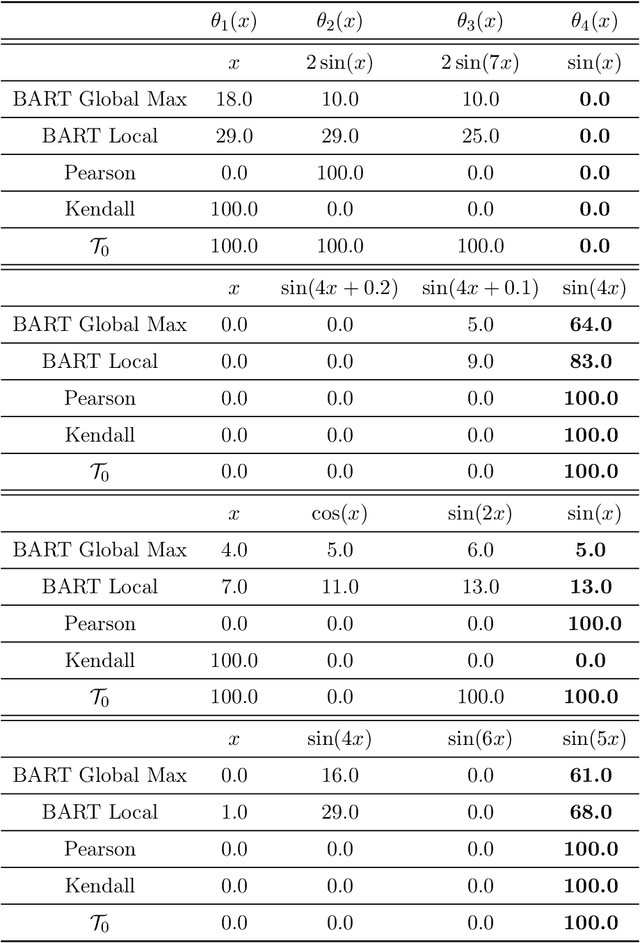
Tree-based methods are powerful nonparametric techniques in statistics and machine learning. However, their effectiveness, particularly in finite-sample settings, is not fully understood. Recent applications have revealed their surprising ability to distinguish transformations (which we call symbolic feature selection) that remain obscure under current theoretical understanding. This work provides a finite-sample analysis of tree-based methods from a ranking perspective. We link oracle partitions in tree methods to response rankings at local splits, offering new insights into their finite-sample behavior in regression and feature selection tasks. Building on this local ranking perspective, we extend our analysis in two ways: (i) We examine the global ranking performance of individual trees and ensembles, including Classification and Regression Trees (CART) and Bayesian Additive Regression Trees (BART), providing finite-sample oracle bounds, ranking consistency, and posterior contraction results. (ii) Inspired by the ranking perspective, we propose concordant divergence statistics $\mathcal{T}_0$ to evaluate symbolic feature mappings and establish their properties. Numerical experiments demonstrate the competitive performance of these statistics in symbolic feature selection tasks compared to existing methods.

Efficient Decision Trees for Tensor Regressions

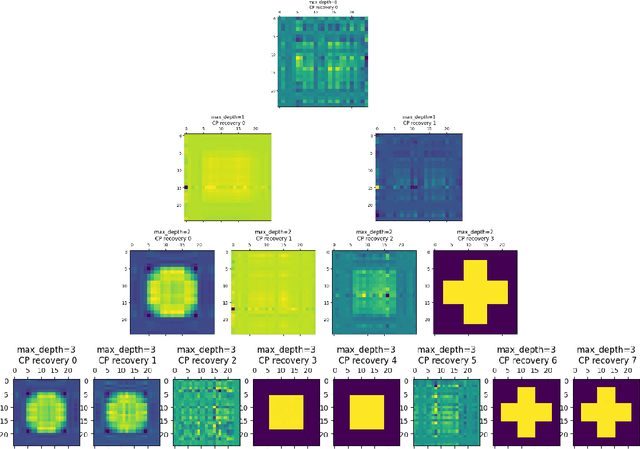
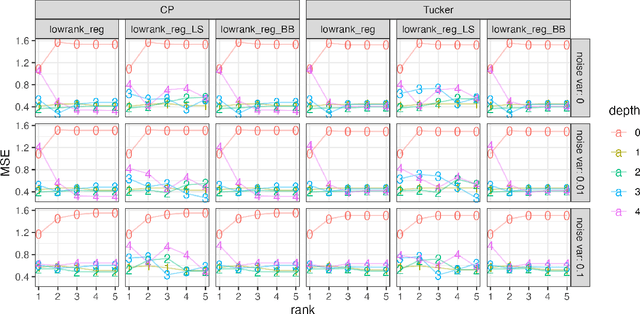
We proposed the tensor-input tree (TT) method for scalar-on-tensor and tensor-on-tensor regression problems. We first address scalar-on-tensor problem by proposing scalar-output regression tree models whose input variable are tensors (i.e., multi-way arrays). We devised and implemented fast randomized and deterministic algorithms for efficient fitting of scalar-on-tensor trees, making TT competitive against tensor-input GP models. Based on scalar-on-tensor tree models, we extend our method to tensor-on-tensor problems using additive tree ensemble approaches. Theoretical justification and extensive experiments on real and synthetic datasets are provided to illustrate the performance of TT.

Topological Learning for Motion Data via Mixed Coordinates

Topology can extract the structural information in a dataset efficiently. In this paper, we attempt to incorporate topological information into a multiple output Gaussian process model for transfer learning purposes. To achieve this goal, we extend the framework of circular coordinates into a novel framework of mixed valued coordinates to take linear trends in the time series into consideration. One of the major challenges to learn from multiple time series effectively via a multiple output Gaussian process model is constructing a functional kernel. We propose to use topologically induced clustering to construct a cluster based kernel in a multiple output Gaussian process model. This kernel not only incorporates the topological structural information, but also allows us to put forward a unified framework using topological information in time and motion series.

A Unifying Perspective on Non-Stationary Kernels for Deeper Gaussian Processes

The Gaussian process (GP) is a popular statistical technique for stochastic function approximation and uncertainty quantification from data. GPs have been adopted into the realm of machine learning in the last two decades because of their superior prediction abilities, especially in data-sparse scenarios, and their inherent ability to provide robust uncertainty estimates. Even so, their performance highly depends on intricate customizations of the core methodology, which often leads to dissatisfaction among practitioners when standard setups and off-the-shelf software tools are being deployed. Arguably the most important building block of a GP is the kernel function which assumes the role of a covariance operator. Stationary kernels of the Mat\'ern class are used in the vast majority of applied studies; poor prediction performance and unrealistic uncertainty quantification are often the consequences. Non-stationary kernels show improved performance but are rarely used due to their more complicated functional form and the associated effort and expertise needed to define and tune them optimally. In this perspective, we want to help ML practitioners make sense of some of the most common forms of non-stationarity for Gaussian processes. We show a variety of kernels in action using representative datasets, carefully study their properties, and compare their performances. Based on our findings, we propose a new kernel that combines some of the identified advantages of existing kernels.

Surrogate-based Autotuning for Randomized Sketching Algorithms in Regression Problems

Algorithms from Randomized Numerical Linear Algebra (RandNLA) are known to be effective in handling high-dimensional computational problems, providing high-quality empirical performance as well as strong probabilistic guarantees. However, their practical application is complicated by the fact that the user needs to set various algorithm-specific tuning parameters which are different than those used in traditional NLA. This paper demonstrates how a surrogate-based autotuning approach can be used to address fundamental problems of parameter selection in RandNLA algorithms. In particular, we provide a detailed investigation of surrogate-based autotuning for sketch-and-precondition (SAP) based randomized least squares methods, which have been one of the great success stories in modern RandNLA. Empirical results show that our surrogate-based autotuning approach can achieve near-optimal performance with much less tuning cost than a random search (up to about 4x fewer trials of different parameter configurations). Moreover, while our experiments focus on least squares, our results demonstrate a general-purpose autotuning pipeline applicable to any kind of RandNLA algorithm.

Sharded Bayesian Additive Regression Trees

In this paper we develop the randomized Sharded Bayesian Additive Regression Trees (SBT) model. We introduce a randomization auxiliary variable and a sharding tree to decide partitioning of data, and fit each partition component to a sub-model using Bayesian Additive Regression Tree (BART). By observing that the optimal design of a sharding tree can determine optimal sharding for sub-models on a product space, we introduce an intersection tree structure to completely specify both the sharding and modeling using only tree structures. In addition to experiments, we also derive the theoretical optimal weights for minimizing posterior contractions and prove the worst-case complexity of SBT.