Efficient Decision Trees for Tensor Regressions

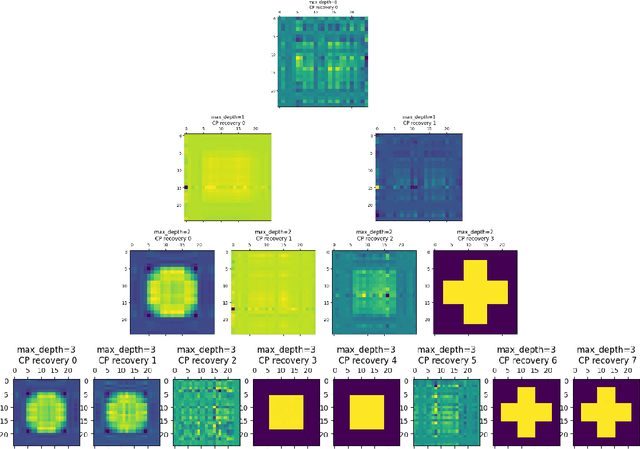
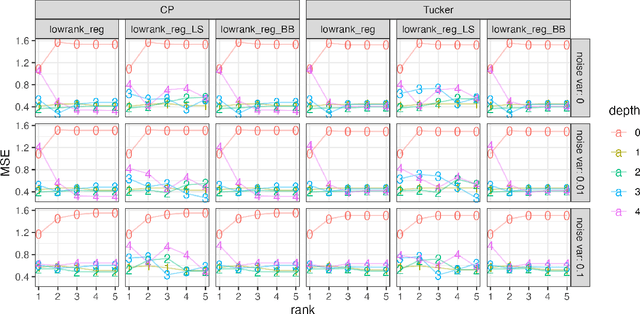
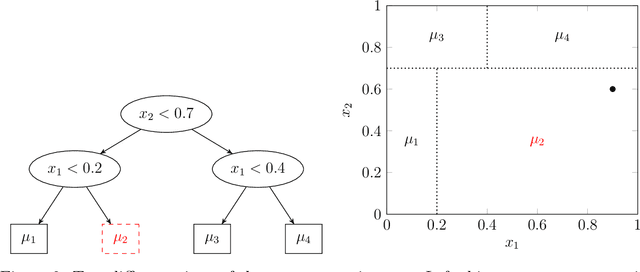
We proposed the tensor-input tree (TT) method for scalar-on-tensor and tensor-on-tensor regression problems. We first address scalar-on-tensor problem by proposing scalar-output regression tree models whose input variable are tensors (i.e., multi-way arrays). We devised and implemented fast randomized and deterministic algorithms for efficient fitting of scalar-on-tensor trees, making TT competitive against tensor-input GP models. Based on scalar-on-tensor tree models, we extend our method to tensor-on-tensor problems using additive tree ensemble approaches. Theoretical justification and extensive experiments on real and synthetic datasets are provided to illustrate the performance of TT.

Using BART for Multiobjective Optimization of Noisy Multiple Objectives

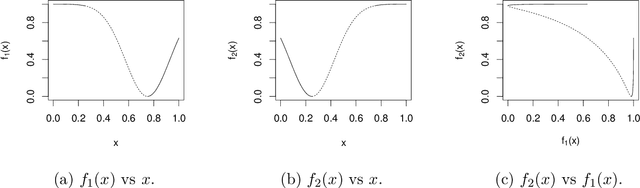
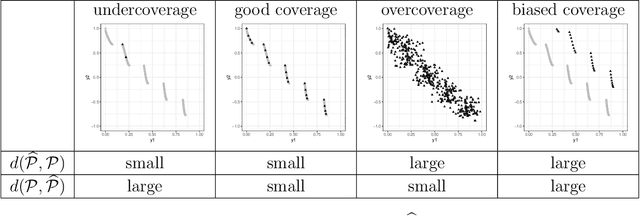
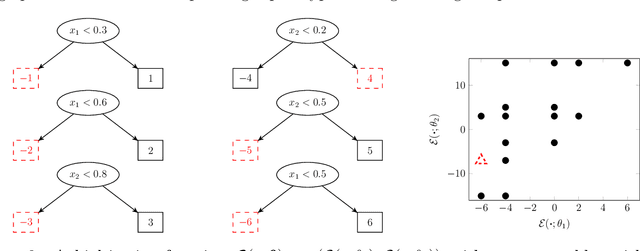
Techniques to reduce the energy burden of an Industry 4.0 ecosystem often require solving a multiobjective optimization problem. However, collecting experimental data can often be either expensive or time-consuming. In such cases, statistical methods can be helpful. This article proposes Pareto Front (PF) and Pareto Set (PS) estimation methods using Bayesian Additive Regression Trees (BART), which is a non-parametric model whose assumptions are typically less restrictive than popular alternatives, such as Gaussian Processes. The performance of our BART-based method is compared to a GP-based method using analytic test functions, demonstrating convincing advantages. Finally, our BART-based methodology is applied to a motivating Industry 4.0 engineering problem.