Sharded Bayesian Additive Regression Trees

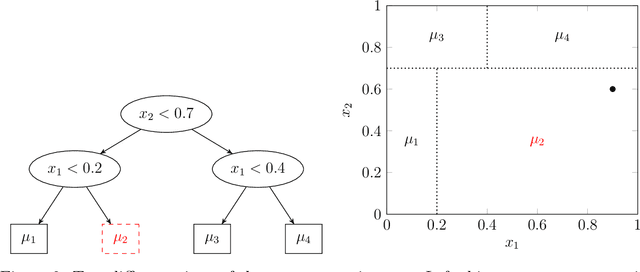
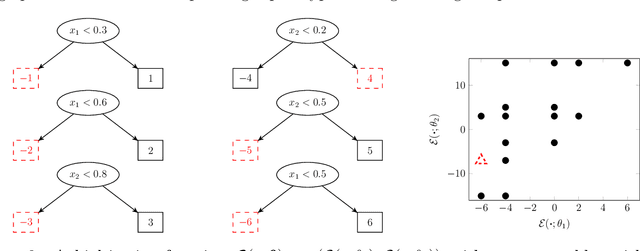
In this paper we develop the randomized Sharded Bayesian Additive Regression Trees (SBT) model. We introduce a randomization auxiliary variable and a sharding tree to decide partitioning of data, and fit each partition component to a sub-model using Bayesian Additive Regression Tree (BART). By observing that the optimal design of a sharding tree can determine optimal sharding for sub-models on a product space, we introduce an intersection tree structure to completely specify both the sharding and modeling using only tree structures. In addition to experiments, we also derive the theoretical optimal weights for minimizing posterior contractions and prove the worst-case complexity of SBT.

Using BART for Multiobjective Optimization of Noisy Multiple Objectives

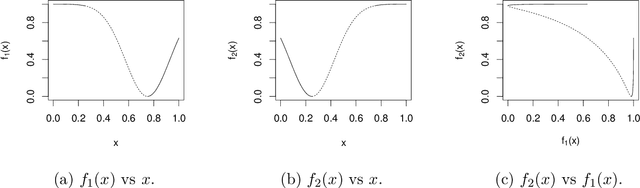
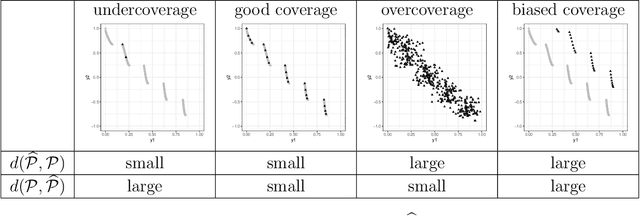
Techniques to reduce the energy burden of an Industry 4.0 ecosystem often require solving a multiobjective optimization problem. However, collecting experimental data can often be either expensive or time-consuming. In such cases, statistical methods can be helpful. This article proposes Pareto Front (PF) and Pareto Set (PS) estimation methods using Bayesian Additive Regression Trees (BART), which is a non-parametric model whose assumptions are typically less restrictive than popular alternatives, such as Gaussian Processes. The performance of our BART-based method is compared to a GP-based method using analytic test functions, demonstrating convincing advantages. Finally, our BART-based methodology is applied to a motivating Industry 4.0 engineering problem.