Ranking Perspective for Tree-based Methods with Applications to Symbolic Feature Selection
Paper and Code
Oct 03, 2024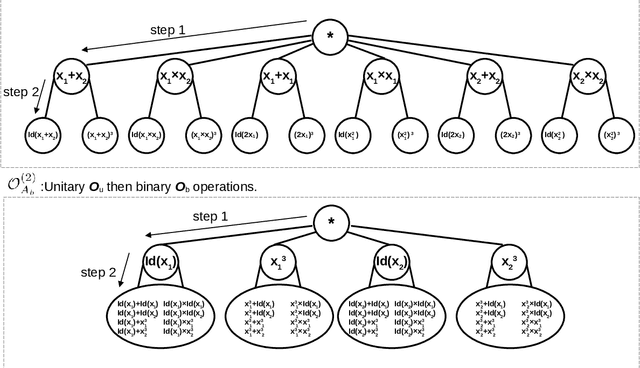
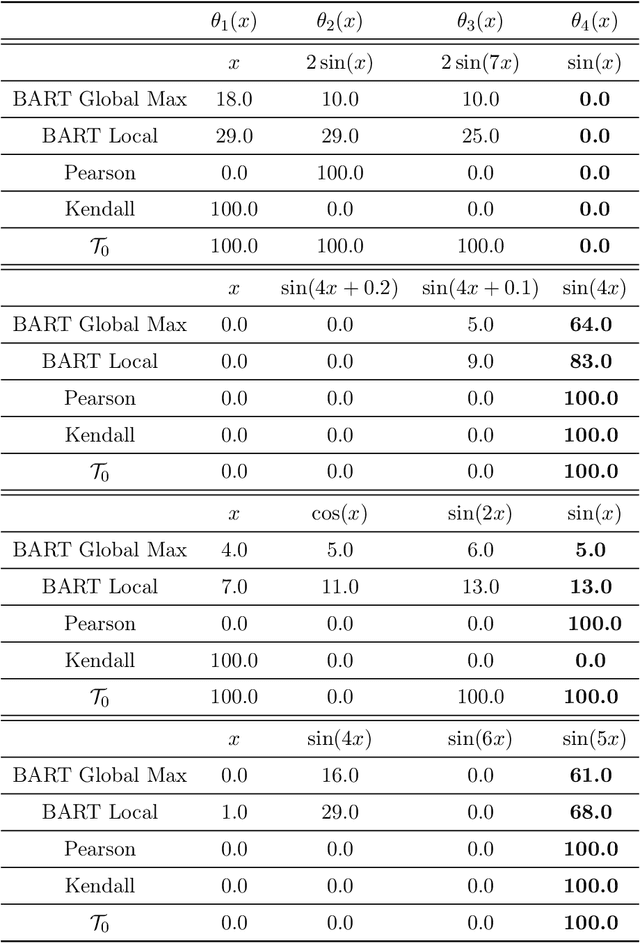
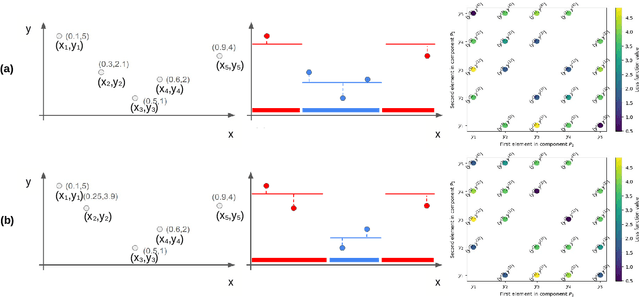

Tree-based methods are powerful nonparametric techniques in statistics and machine learning. However, their effectiveness, particularly in finite-sample settings, is not fully understood. Recent applications have revealed their surprising ability to distinguish transformations (which we call symbolic feature selection) that remain obscure under current theoretical understanding. This work provides a finite-sample analysis of tree-based methods from a ranking perspective. We link oracle partitions in tree methods to response rankings at local splits, offering new insights into their finite-sample behavior in regression and feature selection tasks. Building on this local ranking perspective, we extend our analysis in two ways: (i) We examine the global ranking performance of individual trees and ensembles, including Classification and Regression Trees (CART) and Bayesian Additive Regression Trees (BART), providing finite-sample oracle bounds, ranking consistency, and posterior contraction results. (ii) Inspired by the ranking perspective, we propose concordant divergence statistics $\mathcal{T}_0$ to evaluate symbolic feature mappings and establish their properties. Numerical experiments demonstrate the competitive performance of these statistics in symbolic feature selection tasks compared to existing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge