Mikael Vejdemo-Johansson
Topological Learning for Motion Data via Mixed Coordinates
Oct 30, 2023



Abstract:Topology can extract the structural information in a dataset efficiently. In this paper, we attempt to incorporate topological information into a multiple output Gaussian process model for transfer learning purposes. To achieve this goal, we extend the framework of circular coordinates into a novel framework of mixed valued coordinates to take linear trends in the time series into consideration. One of the major challenges to learn from multiple time series effectively via a multiple output Gaussian process model is constructing a functional kernel. We propose to use topologically induced clustering to construct a cluster based kernel in a multiple output Gaussian process model. This kernel not only incorporates the topological structural information, but also allows us to put forward a unified framework using topological information in time and motion series.
* 7 pages, 4 figures
Generalized Penalty for Circular Coordinate Representation
Jun 03, 2020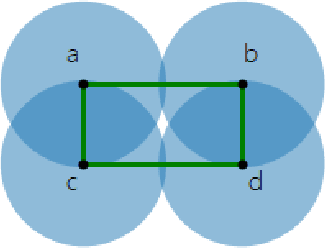
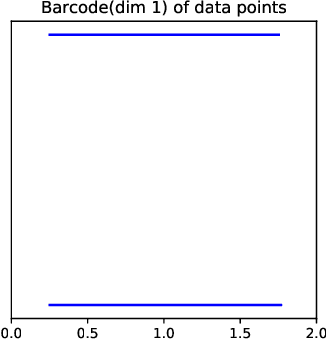
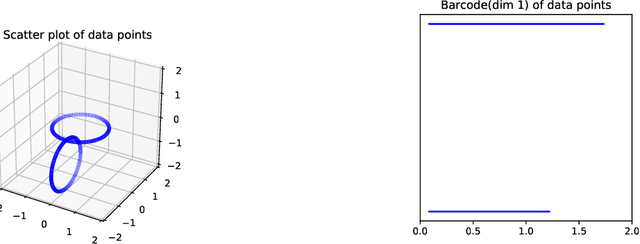
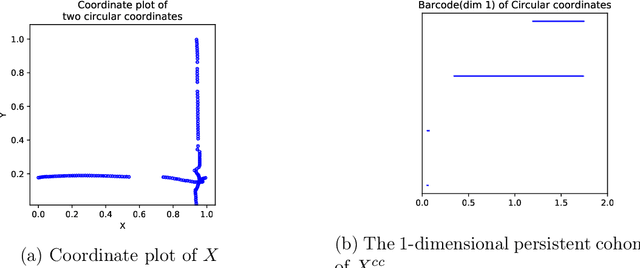
Abstract:Topological Data Analysis (TDA) provides novel approaches that allow us to analyze the geometrical shapes and topological structures of a dataset. As one important application, TDA can be used for data visualization and dimension reduction. We follow the framework of circular coordinate representation, which allows us to perform dimension reduction and visualization for high-dimensional datasets on a torus using persistent cohomology. In this paper, we propose a method to adapt the circular coordinate framework to take into account sparsity in high-dimensional applications. We use a generalized penalty function instead of an $L_{2}$ penalty in the traditional circular coordinate algorithm. We provide simulation experiments and real data analysis to support our claim that circular coordinates with generalized penalty will accommodate the sparsity in high-dimensional datasets under different sampling schemes while preserving the topological structures.
Certified Mapper: Repeated testing for acyclicity and obstructions to the nerve lemma
Aug 29, 2018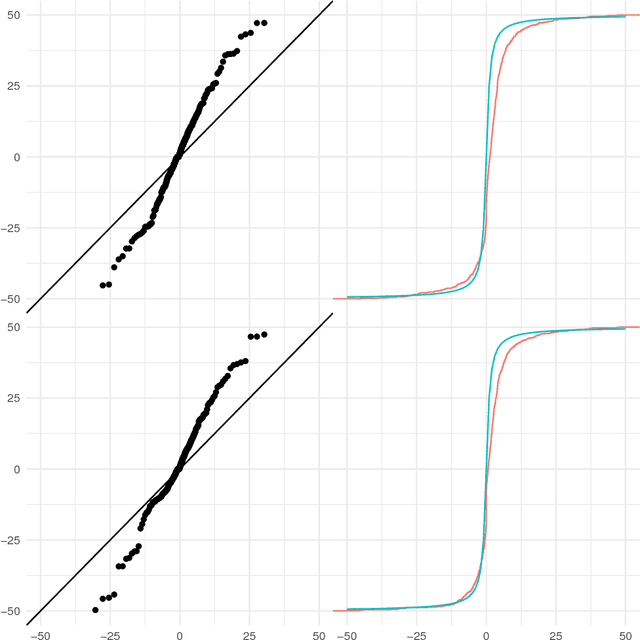
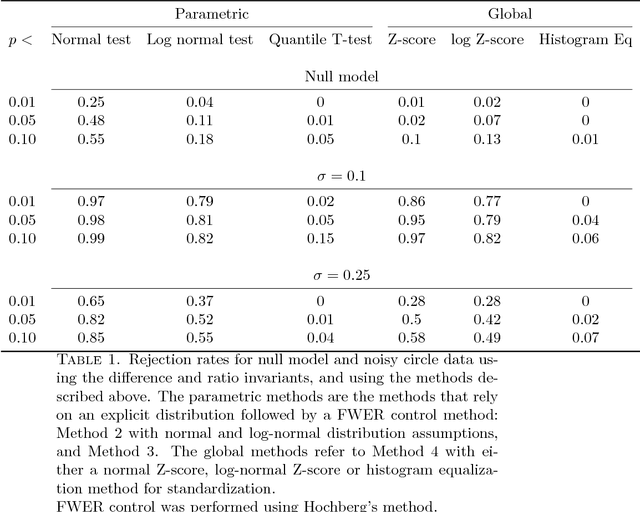
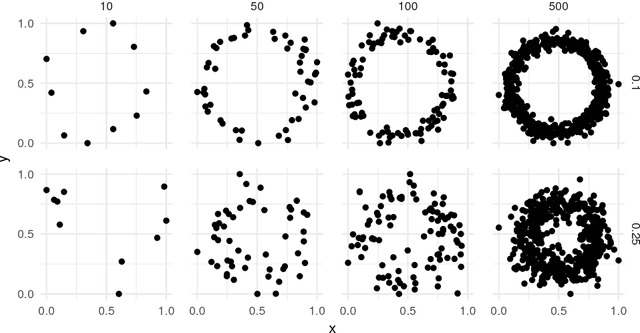

Abstract:The Mapper algorithm does not include a check for whether the cover produced conforms to the requirements of the nerve lemma. To perform a check for obstructions to the nerve lemma, statistical considerations of multiple testing quickly arise. In this paper, we propose several statistical approaches to finding obstructions: through a persistent nerve lemma, through simulation testing, and using a parametric refinement of simulation tests. We suggest Certified Mapper -- a method built from these approaches to generate certificates of non-obstruction, or identify specific obstructions to the nerve lemma -- and we give recommendations for which statistical approaches are most appropriate for the task.
Fibres of Failure: Classifying errors in predictive processes
Feb 09, 2018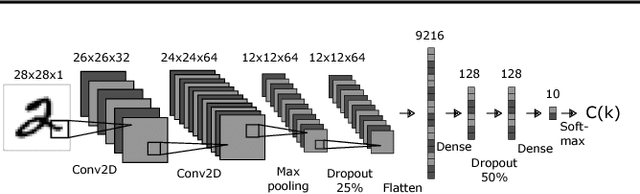



Abstract:We describe Fibres of Failure (FiFa), a method to classify failure modes of predictive processes using the Mapper algorithm from Topological Data Analysis. Our method uses Mapper to build a graph model of input data stratified by prediction error. Groupings found in high-error regions of the Mapper model then provide distinct failure modes of the predictive process. We demonstrate FiFa on misclassifications of MNIST images with added noise, and demonstrate two ways to use the failure mode classification: either to produce a correction layer that adjusts predictions by similarity to the failure modes; or to inspect members of the failure modes to illustrate and investigate what characterizes each failure mode.
Automatic recognition and tagging of topologically different regimes in dynamical systems
Mar 24, 2014
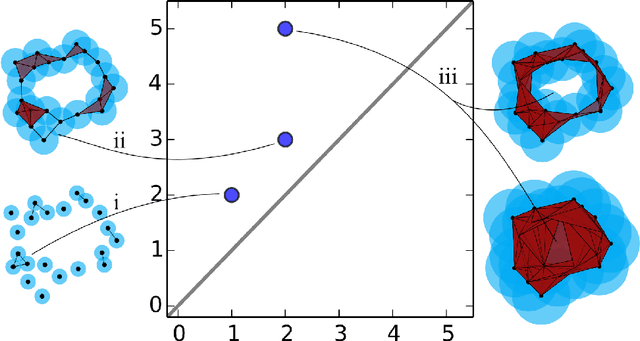
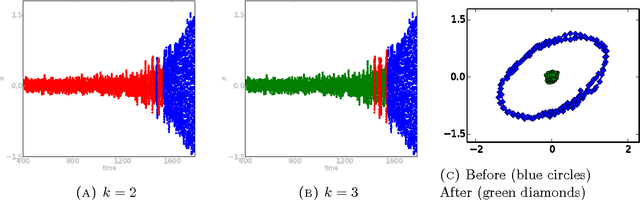
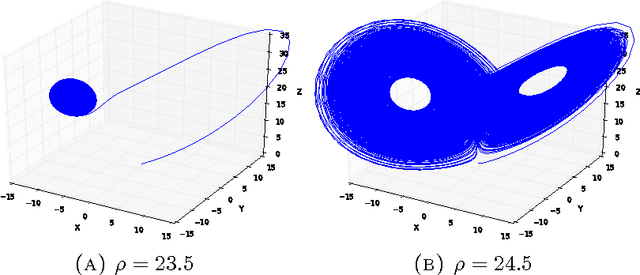
Abstract:Complex systems are commonly modeled using nonlinear dynamical systems. These models are often high-dimensional and chaotic. An important goal in studying physical systems through the lens of mathematical models is to determine when the system undergoes changes in qualitative behavior. A detailed description of the dynamics can be difficult or impossible to obtain for high-dimensional and chaotic systems. Therefore, a more sensible goal is to recognize and mark transitions of a system between qualitatively different regimes of behavior. In practice, one is interested in developing techniques for detection of such transitions from sparse observations, possibly contaminated by noise. In this paper we develop a framework to accurately tag different regimes of complex systems based on topological features. In particular, our framework works with a high degree of success in picking out a cyclically orbiting regime from a stationary equilibrium regime in high-dimensional stochastic dynamical systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge