Kernel-based estimators for functional causal effects

We propose causal effect estimators based on empirical Fr\'{e}chet means and operator-valued kernels, tailored to functional data spaces. These methods address the challenges of high-dimensionality, sequential ordering, and model complexity while preserving robustness to treatment misspecification. Using structural assumptions, we obtain compact representations of potential outcomes, enabling scalable estimation of causal effects over time and across covariates. We provide both theoretical, regarding the consistency of functional causal effects, as well as empirical comparison of a range of proposed causal effect estimators. Applications to binary treatment settings with functional outcomes illustrate the framework's utility in biomedical monitoring, where outcomes exhibit complex temporal dynamics. Our estimators accommodate scenarios with registered covariates and outcomes, aligning them to the Fr\'{e}chet means, as well as cases requiring higher-order representations to capture intricate covariate-outcome interactions. These advancements extend causal inference to dynamic and non-linear domains, offering new tools for understanding complex treatment effects in functional data settings.

Hypergraphon Mean Field Games

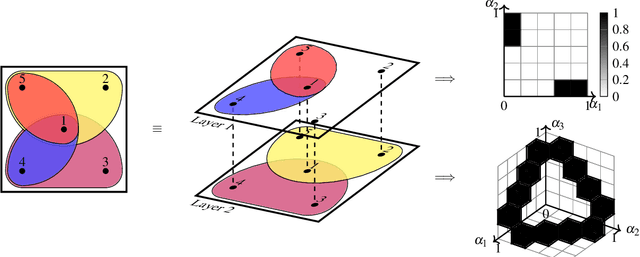
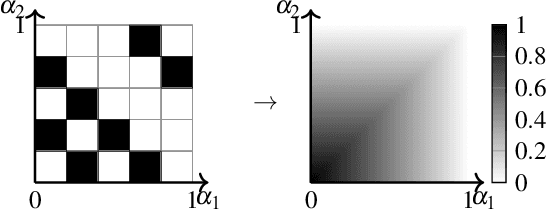
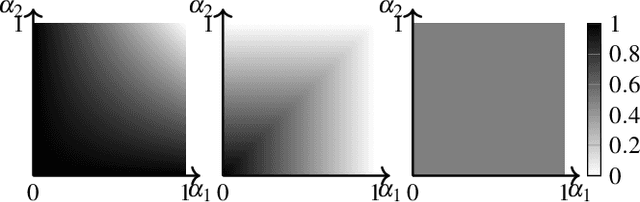
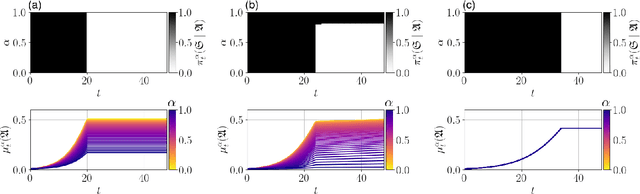
We propose an approach to modelling large-scale multi-agent dynamical systems allowing interactions among more than just pairs of agents using the theory of mean-field games and the notion of hypergraphons, which are obtained as limits of large hypergraphs. To the best of our knowledge, ours is the first work on mean field games on hypergraphs. Together with an extension to a multi-layer setup, we obtain limiting descriptions for large systems of non-linear, weakly-interacting dynamical agents. On the theoretical side, we prove the well-foundedness of the resulting hypergraphon mean field game, showing both existence and approximate Nash properties. On the applied side, we extend numerical and learning algorithms to compute the hypergraphon mean field equilibria. To verify our approach empirically, we consider an epidemic control problem and a social rumor spreading model, where we give agents intrinsic motivation to spread rumors to unaware agents.

Inverse Reinforcement Learning in Swarm Systems

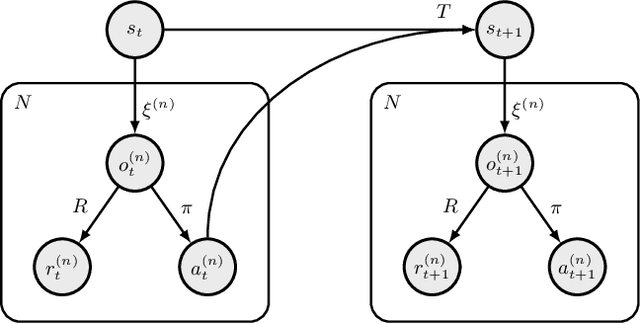
Inverse reinforcement learning (IRL) has become a useful tool for learning behavioral models from demonstration data. However, IRL remains mostly unexplored for multi-agent systems. In this paper, we show how the principle of IRL can be extended to homogeneous large-scale problems, inspired by the collective swarming behavior of natural systems. In particular, we make the following contributions to the field: 1) We introduce the swarMDP framework, a sub-class of decentralized partially observable Markov decision processes endowed with a swarm characterization. 2) Exploiting the inherent homogeneity of this framework, we reduce the resulting multi-agent IRL problem to a single-agent one by proving that the agent-specific value functions in this model coincide. 3) To solve the corresponding control problem, we propose a novel heterogeneous learning scheme that is particularly tailored to the swarm setting. Results on two example systems demonstrate that our framework is able to produce meaningful local reward models from which we can replicate the observed global system dynamics.