Abdelhak M. Zoubir
Sensitivity Curve Maximization: Attacking Robust Aggregators in Distributed Learning
Dec 23, 2024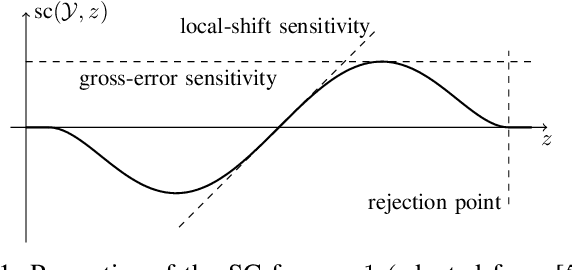
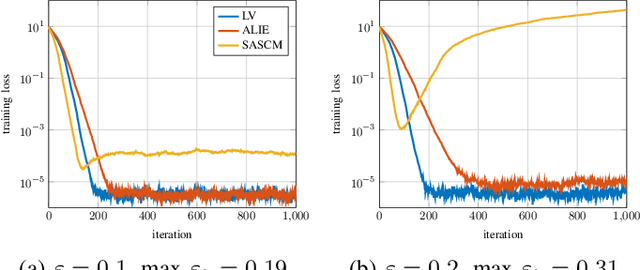
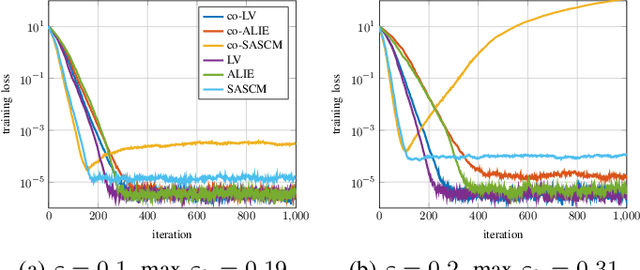
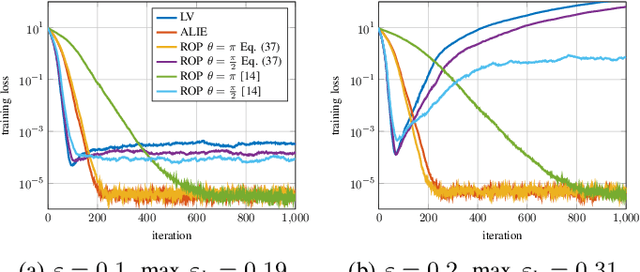
Abstract:In distributed learning agents aim at collaboratively solving a global learning problem. It becomes more and more likely that individual agents are malicious or faulty with an increasing size of the network. This leads to a degeneration or complete breakdown of the learning process. Classical aggregation schemes are prone to breakdown at small contamination rates, therefore robust aggregation schemes are sought for. While robust aggregation schemes can generally tolerate larger contamination rates, many have been shown to be susceptible to carefully crafted malicious attacks. In this work, we show how the sensitivity curve (SC), a classical tool from robust statistics, can be used to systematically derive optimal attack patterns against arbitrary robust aggregators, in most cases rendering them ineffective. We show the effectiveness of the proposed attack in multiple simulations.
Fronthaul-Constrained Distributed Radar Sensing
Sep 26, 2024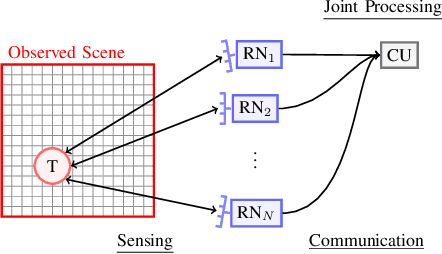
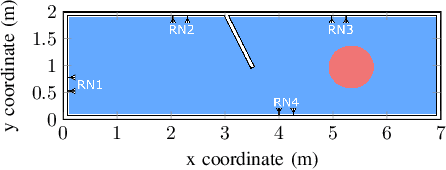
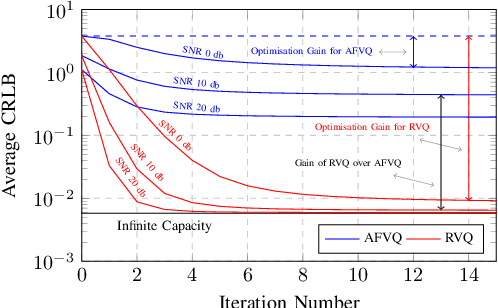
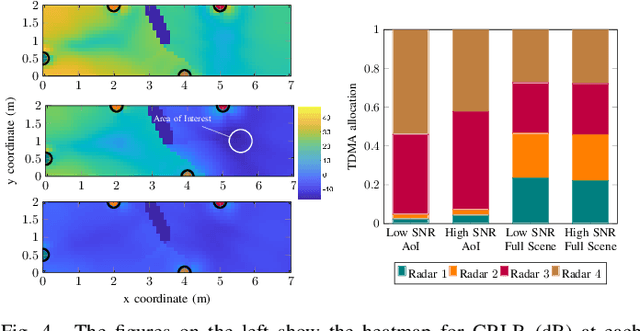
Abstract:In this paper, we study a network of distributed radar sensors that collaboratively perform sensing tasks by transmitting their quantized radar signals over capacity-constrained fronthaul links to a central unit for joint processing. We consider per-antenna and per-radar vector quantization and fronthaul links with dedicated resources as well as shared resources based on time-division multiple access. For this setting, we formulate a joint optimization problem for fronthaul compression and time allocation that minimizes the Cramer Rao bound of the aggregated radar signals at the central unit. Since the problem does not admit a standard form that can be solved by existing commercial numerical solvers, we propose refomulations that enable us to develop an efficient suboptimal algorithm based on semidefinite programming and alternating convex optimization. Moreover, we analyze the convergence and complexity of the proposed algorithm. Simulation results confirm that a significant performance gain can be achieved by distributed sensing, particularly in practical scenarios where one radar may not have a sufficient view of all the scene. Furthermore, the simulation results suggest that joint fronthaul compression and time allocation are crucial for efficient exploitation of the limited fronthaul capacity.
A Graph Signal Processing Perspective of Network Multiple Hypothesis Testing with False Discovery Rate Control
Aug 06, 2024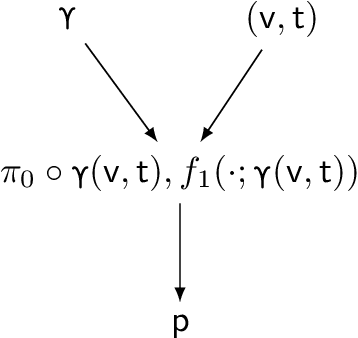
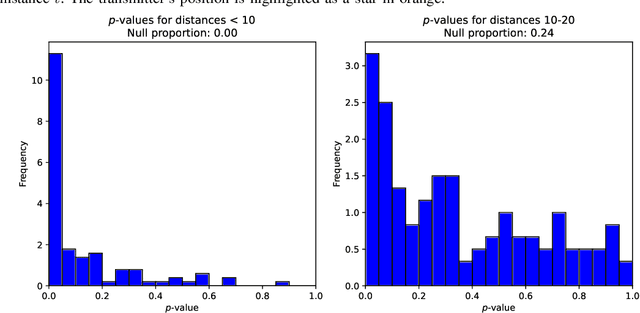
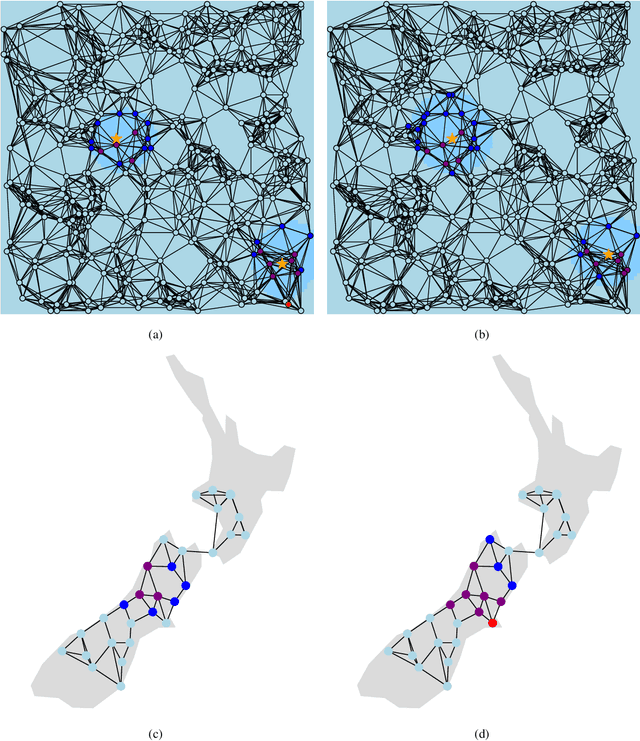
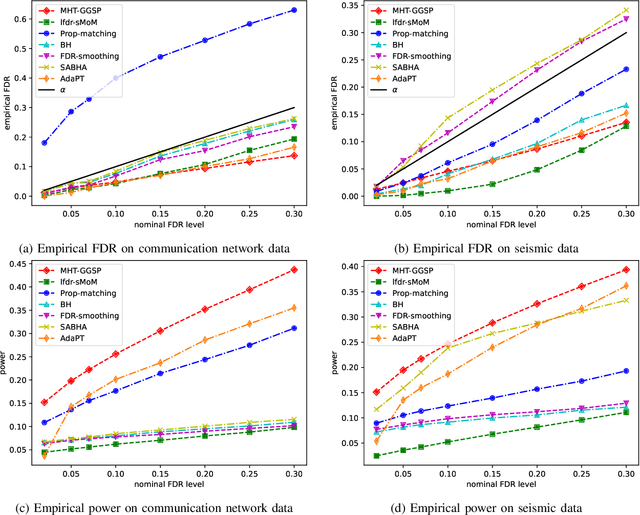
Abstract:We consider a multiple hypothesis testing problem in a sensor network over the joint spatial-time domain. The sensor network is modeled as a graph, with each vertex representing a sensor and a signal over time associated with each vertex. We assume a hypothesis test and an associated p-value for every sample point in the joint spatial-time domain. Our goal is to determine which points have true alternative hypotheses. By parameterizing the unknown alternative distribution of $p$-values and the prior probabilities of hypotheses being null with a bandlimited generalized graph signal, we can obtain consistent estimates for them. Consequently, we also obtain an estimate of the local false discovery rates (lfdr). We prove that by using a step-up procedure on the estimated lfdr, we can achieve asymptotic false discovery rate control at a pre-determined level. Numerical experiments validate the effectiveness of our approach compared to existing methods.
Fast and Robust Sparsity-Aware Block Diagonal Representation
Dec 02, 2023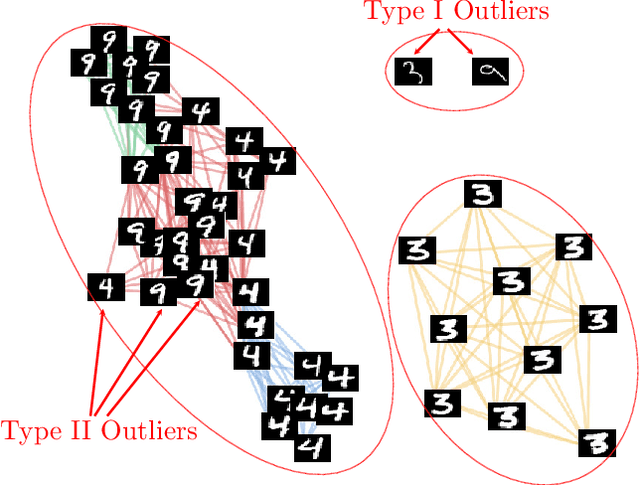
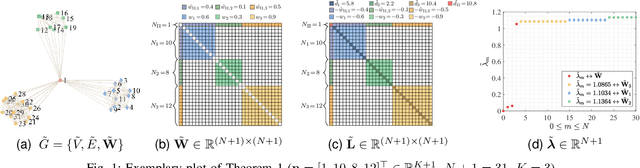
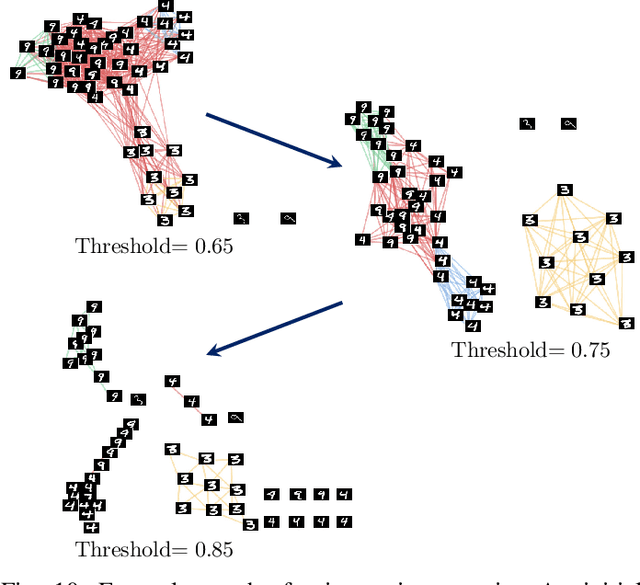
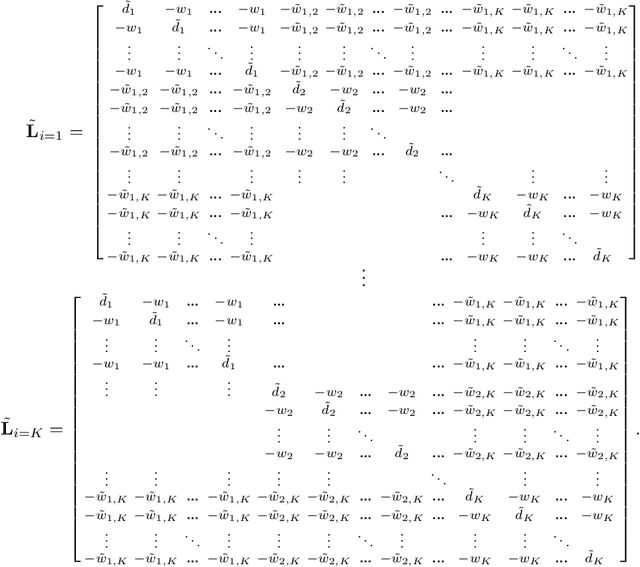
Abstract:The block diagonal structure of an affinity matrix is a commonly desired property in cluster analysis because it represents clusters of feature vectors by non-zero coefficients that are concentrated in blocks. However, recovering a block diagonal affinity matrix is challenging in real-world applications, in which the data may be subject to outliers and heavy-tailed noise that obscure the hidden cluster structure. To address this issue, we first analyze the effect of different fundamental outlier types in graph-based cluster analysis. A key idea that simplifies the analysis is to introduce a vector that represents a block diagonal matrix as a piece-wise linear function of the similarity coefficients that form the affinity matrix. We reformulate the problem as a robust piece-wise linear fitting problem and propose a Fast and Robust Sparsity-Aware Block Diagonal Representation (FRS-BDR) method, which jointly estimates cluster memberships and the number of blocks. Comprehensive experiments on a variety of real-world applications demonstrate the effectiveness of FRS-BDR in terms of clustering accuracy, robustness against corrupted features, computation time and cluster enumeration performance.
Attentional Graph Neural Networks for Robust Massive Network Localization
Nov 28, 2023



Abstract:Graph neural networks (GNNs) have gained significant popularity for classification tasks in machine learning, yet their applications to regression problems remain limited. Concurrently, attention mechanisms have emerged as powerful tools in sequential learning tasks. In this paper, we employ GNNs and attention mechanisms to address a classical but challenging nonlinear regression problem: network localization. We propose a novel GNN-based network localization method that achieves exceptional stability and accuracy in the presence of severe non-line-of-sight (NLOS) propagations, while eliminating the need for laborious offline calibration or NLOS identification. Extensive experimental results validate the effectiveness and high accuracy of our GNN-based localization model, particularly in challenging NLOS scenarios. However, the proposed GNN-based model exhibits limited flexibility, and its accuracy is highly sensitive to a specific hyperparameter that determines the graph structure. To address the limitations and extend the applicability of the GNN-based model to real scenarios, we introduce two attentional graph neural networks (AGNNs) that offer enhanced flexibility and the ability to automatically learn the optimal hyperparameter for each node. Experimental results confirm that the AGNN models are able to enhance localization accuracy, providing a promising solution for real-world applications. We also provide some analyses of the improved performance achieved by the AGNN models from the perspectives of dynamic attention and signal denoising characteristics.
Low-Rank Tensor Completion via Novel Sparsity-Inducing Regularizers
Oct 10, 2023Abstract:To alleviate the bias generated by the l1-norm in the low-rank tensor completion problem, nonconvex surrogates/regularizers have been suggested to replace the tensor nuclear norm, although both can achieve sparsity. However, the thresholding functions of these nonconvex regularizers may not have closed-form expressions and thus iterations are needed, which increases the computational loads. To solve this issue, we devise a framework to generate sparsity-inducing regularizers with closed-form thresholding functions. These regularizers are applied to low-tubal-rank tensor completion, and efficient algorithms based on the alternating direction method of multipliers are developed. Furthermore, convergence of our methods is analyzed and it is proved that the generated sequences are bounded and any limit point is a stationary point. Experimental results using synthetic and real-world datasets show that the proposed algorithms outperform the state-of-the-art methods in terms of restoration performance.
Robust Low-Rank Matrix Completion via a New Sparsity-Inducing Regularizer
Oct 07, 2023Abstract:This paper presents a novel loss function referred to as hybrid ordinary-Welsch (HOW) and a new sparsity-inducing regularizer associated with HOW. We theoretically show that the regularizer is quasiconvex and that the corresponding Moreau envelope is convex. Moreover, the closed-form solution to its Moreau envelope, namely, the proximity operator, is derived. Compared with nonconvex regularizers like the lp-norm with 0<p<1 that requires iterations to find the corresponding proximity operator, the developed regularizer has a closed-form proximity operator. We apply our regularizer to the robust matrix completion problem, and develop an efficient algorithm based on the alternating direction method of multipliers. The convergence of the suggested method is analyzed and we prove that any generated accumulation point is a stationary point. Finally, experimental results based on synthetic and real-world datasets demonstrate that our algorithm is superior to the state-of-the-art methods in terms of restoration performance.
Identifying the Complete Correlation Structure in Large-Scale High-Dimensional Data Sets with Local False Discovery Rates
Jun 01, 2023
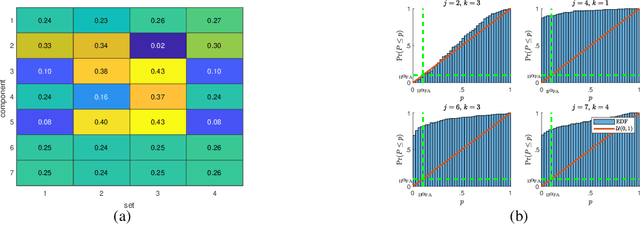
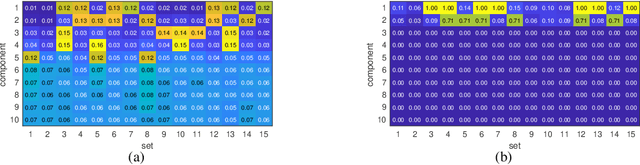
Abstract:The identification of the dependent components in multiple data sets is a fundamental problem in many practical applications. The challenge in these applications is that often the data sets are high-dimensional with few observations or available samples and contain latent components with unknown probability distributions. A novel mathematical formulation of this problem is proposed, which enables the inference of the underlying correlation structure with strict false positive control. In particular, the false discovery rate is controlled at a pre-defined threshold on two levels simultaneously. The deployed test statistics originate in the sample coherence matrix. The required probability models are learned from the data using the bootstrap. Local false discovery rates are used to solve the multiple hypothesis testing problem. Compared to the existing techniques in the literature, the developed technique does not assume an a priori correlation structure and work well when the number of data sets is large while the number of observations is small. In addition, it can handle the presence of distributional uncertainties, heavy-tailed noise, and outliers.
Emergency Response Person Localization and Vital Sign Estimation Using a Semi-Autonomous Robot Mounted SFCW Radar
May 25, 2023



Abstract:The large number and scale of natural and man-made disasters have led to an urgent demand for technologies that enhance the safety and efficiency of search and rescue teams. Semi-autonomous rescue robots are beneficial, especially when searching inaccessible terrains, or dangerous environments, such as collapsed infrastructures. For search and rescue missions in degraded visual conditions or non-line of sight scenarios, radar-based approaches may contribute to acquire valuable, and otherwise unavailable information. This article presents a complete signal processing chain for radar-based multi-person detection, 2D-MUSIC localization and breathing frequency estimation. The proposed method shows promising results on a challenging emergency response dataset that we collected using a semi-autonomous robot equipped with a commercially available through-wall radar system. The dataset is composed of 62 scenarios of various difficulty levels with up to five persons captured in different postures, angles and ranges including wooden and stone obstacles that block the radar line of sight. Ground truth data for reference locations, respiration, electrocardiogram, and acceleration signals are included. The full emergency response benchmark data set as well as all codes to reproduce our results, are publicly available at https://doi.org/10.21227/4bzd-jm32.
Attacks on Robust Distributed Learning Schemes via Sensitivity Curve Maximization
Apr 27, 2023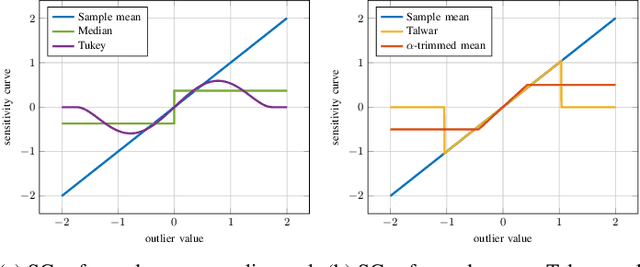
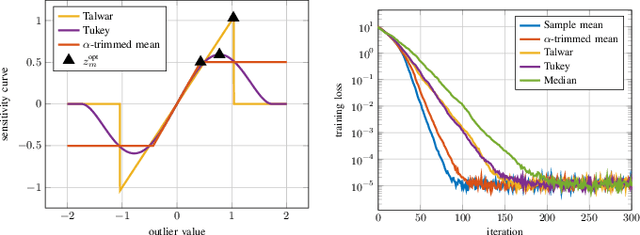
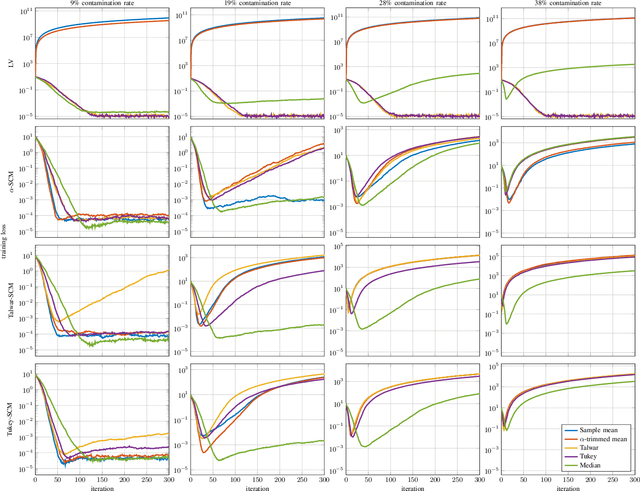
Abstract:Distributed learning paradigms, such as federated or decentralized learning, allow a collection of agents to solve global learning and optimization problems through limited local interactions. Most such strategies rely on a mixture of local adaptation and aggregation steps, either among peers or at a central fusion center. Classically, aggregation in distributed learning is based on averaging, which is statistically efficient, but susceptible to attacks by even a small number of malicious agents. This observation has motivated a number of recent works, which develop robust aggregation schemes by employing robust variations of the mean. We present a new attack based on sensitivity curve maximization (SCM), and demonstrate that it is able to disrupt existing robust aggregation schemes by injecting small, but effective perturbations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge