Stefan Vlaski
Graph-Aware Learning Rates for Decentralized Optimization
Sep 18, 2025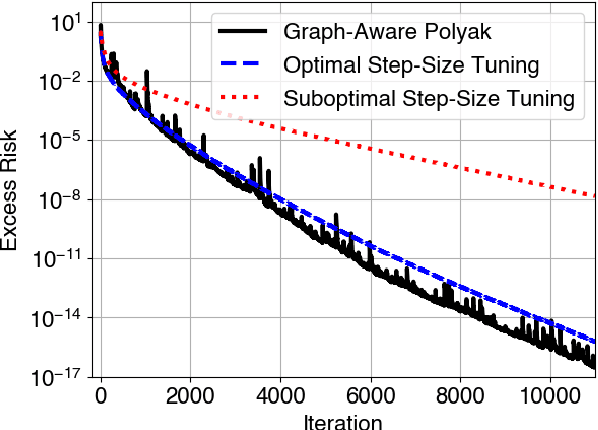
Abstract:We propose an adaptive step-size rule for decentralized optimization. Choosing a step-size that balances convergence and stability is challenging. This is amplified in the decentralized setting as agents observe only local (possibly stochastic) gradients and global information (like smoothness) is unavailable. We derive a step-size rule from first principles. The resulting formulation reduces to the well-known Polyak's rule in the single-agent setting, and is suitable for use with stochastic gradients. The method is parameter free, apart from requiring the optimal objective value, which is readily available in many applications. Numerical simulations demonstrate that the performance is comparable to the optimally fine-tuned step-size.
On the Convergence of Decentralized Stochastic Gradient-Tracking with Finite-Time Consensus
May 29, 2025Abstract:Algorithms for decentralized optimization and learning rely on local optimization steps coupled with combination steps over a graph. Recent works have demonstrated that using a time-varying sequence of matrices that achieve finite-time consensus can improve the communication and iteration complexity of decentralized optimization algorithms based on gradient tracking. In practice, a sequence of matrices satisfying the exact finite-time consensus property may not be available due to imperfect knowledge of the network topology, a limit on the length of the sequence, or numerical instabilities. In this work, we quantify the impact of approximate finite-time consensus sequences on the convergence of a gradient-tracking based decentralized optimization algorithm, clarifying the interplay between accuracy and length of the sequence as well as typical problem parameters such as smoothness and gradient noise.
Convergence Analysis of alpha-SVRG under Strong Convexity
Mar 16, 2025Abstract:Stochastic first-order methods for empirical risk minimization employ gradient approximations based on sampled data in lieu of exact gradients. Such constructions introduce noise into the learning dynamics, which can be corrected through variance-reduction techniques. There is increasing evidence in the literature that in many modern learning applications noise can have a beneficial effect on optimization and generalization. To this end, the recently proposed variance-reduction technique, alpha-SVRG [Yin et al., 2023] allows for fine-grained control of the level of residual noise in the learning dynamics, and has been reported to empirically outperform both SGD and SVRG in modern deep learning scenarios. By focusing on strongly convex environments, we first provide a unified convergence rate expression for alpha-SVRG under fixed learning rate, which reduces to that of either SGD or SVRG by setting alpha=0 or alpha=1, respectively. We show that alpha-SVRG has faster convergence rate compared to SGD and SVRG under suitable choice of alpha. Simulation results on linear regression validate our theory.
Decentralized Learning with Approximate Finite-Time Consensus
Jan 14, 2025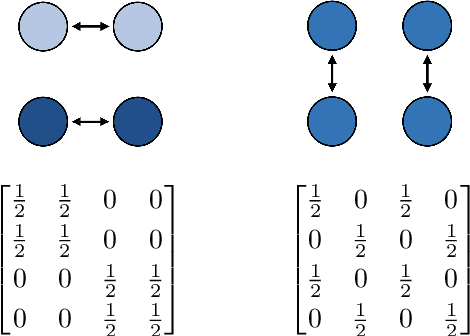
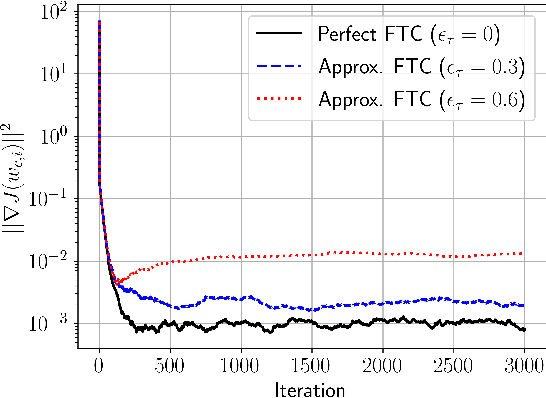
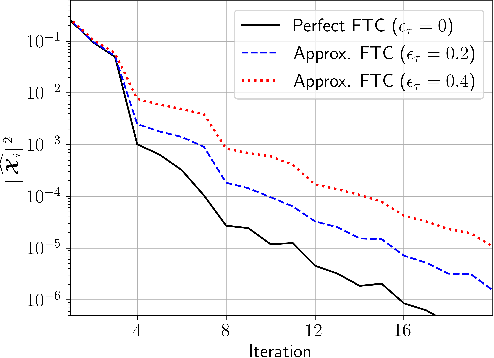
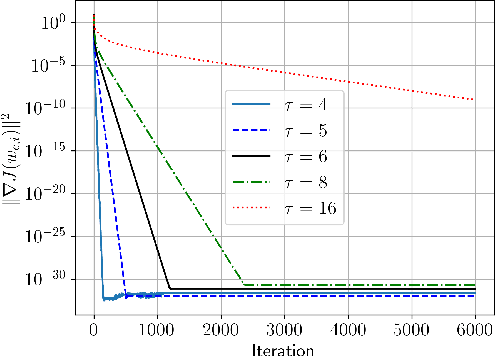
Abstract:The performance of algorithms for decentralized optimization is affected by both the optimization error and the consensus error, the latter of which arises from the variation between agents' local models. Classically, algorithms employ averaging and gradient-tracking mechanisms with constant combination matrices to drive the collection of agents to consensus. Recent works have demonstrated that using sequences of combination matrices that achieve finite-time consensus (FTC) can result in improved communication efficiency or iteration complexity for decentralized optimization. Notably, these studies apply to highly structured networks, where exact finite-time consensus sequences are known exactly and in closed form. In this work we investigate the impact of utilizing approximate FTC matrices in decentralized learning algorithms, and quantify the impact of the approximation error on convergence rate and steady-state performance. Approximate FTC matrices can be inferred for general graphs and do not rely on a particular graph structure or prior knowledge, making the proposed scheme applicable to a broad range of decentralized learning settings.
Deep-Relative-Trust-Based Diffusion for Decentralized Deep Learning
Jan 06, 2025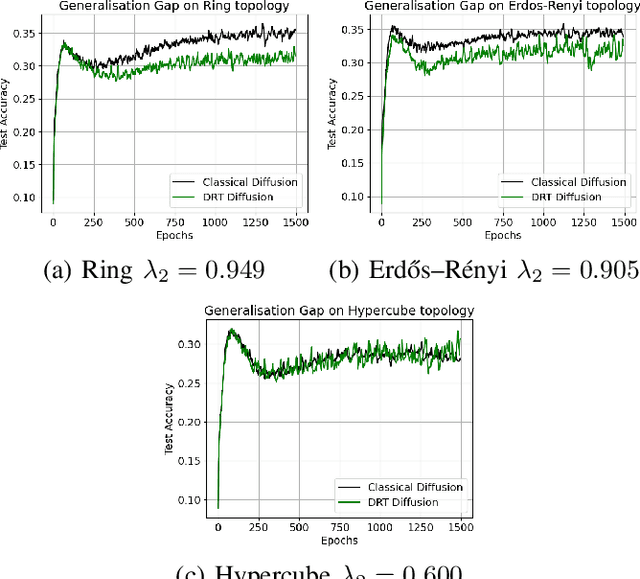
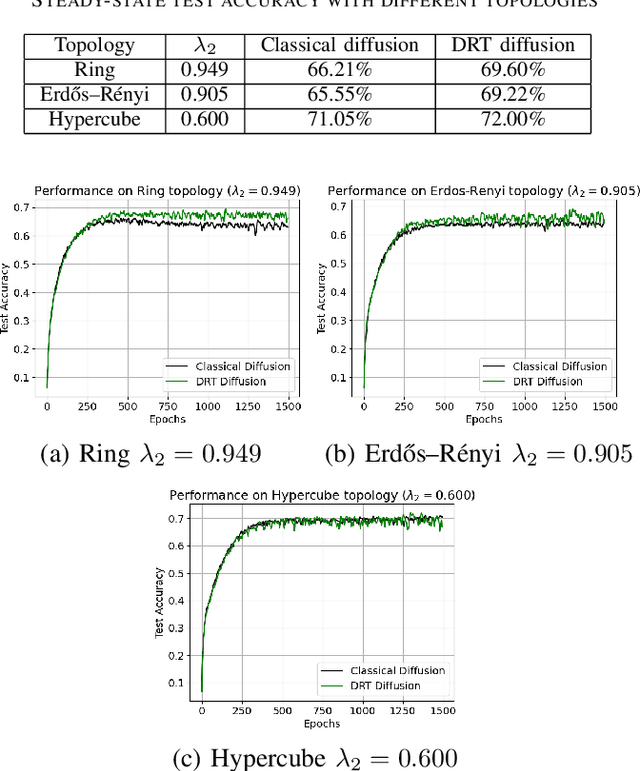
Abstract:Decentralized learning strategies allow a collection of agents to learn efficiently from local data sets without the need for central aggregation or orchestration. Current decentralized learning paradigms typically rely on an averaging mechanism to encourage agreement in the parameter space. We argue that in the context of deep neural networks, which are often over-parameterized, encouraging consensus of the neural network outputs, as opposed to their parameters can be more appropriate. This motivates the development of a new decentralized learning algorithm, termed DRT diffusion, based on deep relative trust (DRT), a recently introduced similarity measure for neural networks. We provide convergence analysis for the proposed strategy, and numerically establish its benefit to generalization, especially with sparse topologies, in an image classification task.
Sensitivity Curve Maximization: Attacking Robust Aggregators in Distributed Learning
Dec 23, 2024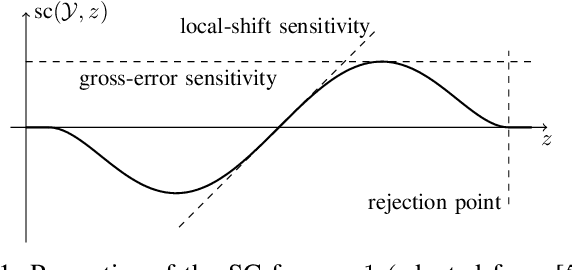
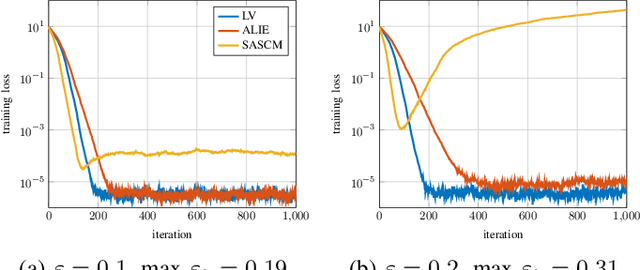
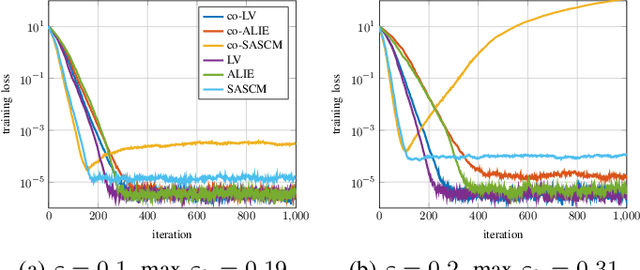
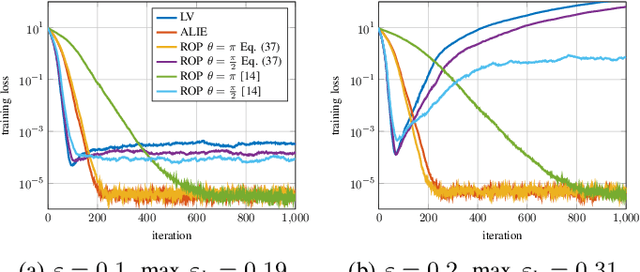
Abstract:In distributed learning agents aim at collaboratively solving a global learning problem. It becomes more and more likely that individual agents are malicious or faulty with an increasing size of the network. This leads to a degeneration or complete breakdown of the learning process. Classical aggregation schemes are prone to breakdown at small contamination rates, therefore robust aggregation schemes are sought for. While robust aggregation schemes can generally tolerate larger contamination rates, many have been shown to be susceptible to carefully crafted malicious attacks. In this work, we show how the sensitivity curve (SC), a classical tool from robust statistics, can be used to systematically derive optimal attack patterns against arbitrary robust aggregators, in most cases rendering them ineffective. We show the effectiveness of the proposed attack in multiple simulations.
Differential error feedback for communication-efficient decentralized learning
Jun 26, 2024



Abstract:Communication-constrained algorithms for decentralized learning and optimization rely on local updates coupled with the exchange of compressed signals. In this context, differential quantization is an effective technique to mitigate the negative impact of compression by leveraging correlations between successive iterates. In addition, the use of error feedback, which consists of incorporating the compression error into subsequent steps, is a powerful mechanism to compensate for the bias caused by the compression. Under error feedback, performance guarantees in the literature have so far focused on algorithms employing a fusion center or a special class of contractive compressors that cannot be implemented with a finite number of bits. In this work, we propose a new decentralized communication-efficient learning approach that blends differential quantization with error feedback. The approach is specifically tailored for decentralized learning problems where agents have individual risk functions to minimize subject to subspace constraints that require the minimizers across the network to lie in low-dimensional subspaces. This constrained formulation includes consensus or single-task optimization as special cases, and allows for more general task relatedness models such as multitask smoothness and coupled optimization. We show that, under some general conditions on the compression noise, and for sufficiently small step-sizes $\mu$, the resulting communication-efficient strategy is stable both in terms of mean-square error and average bit rate: by reducing $\mu$, it is possible to keep the estimation errors small (on the order of $\mu$) without increasing indefinitely the bit rate as $\mu\rightarrow 0$. The results establish that, in the small step-size regime and with a finite number of bits, it is possible to attain the performance achievable in the absence of compression.
Learned Finite-Time Consensus for Distributed Optimization
Apr 10, 2024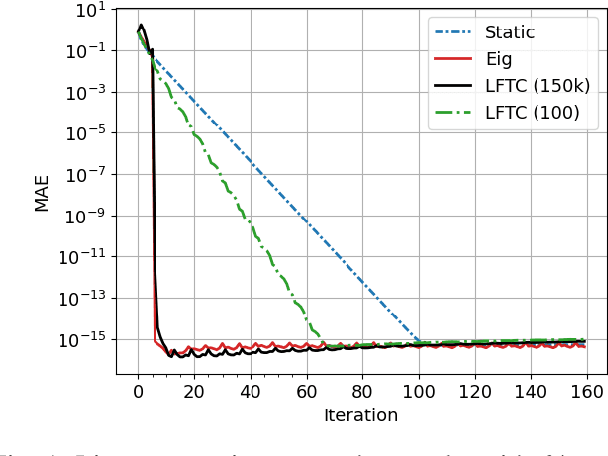
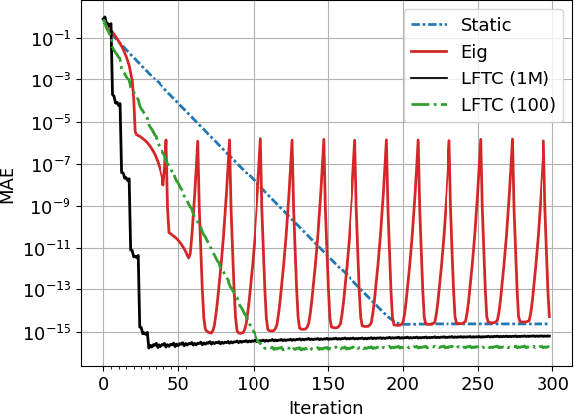
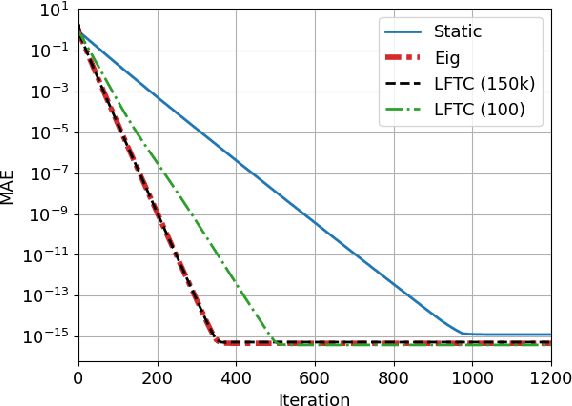
Abstract:Most algorithms for decentralized learning employ a consensus or diffusion mechanism to drive agents to a common solution of a global optimization problem. Generally this takes the form of linear averaging, at a rate of contraction determined by the mixing rate of the underlying network topology. For very sparse graphs this can yield a bottleneck, slowing down the convergence of the learning algorithm. We show that a sequence of matrices achieving finite-time consensus can be learned for unknown graph topologies in a decentralized manner by solving a constrained matrix factorization problem. We demonstrate numerically the benefit of the resulting scheme in both structured and unstructured graphs.
Attacks on Robust Distributed Learning Schemes via Sensitivity Curve Maximization
Apr 27, 2023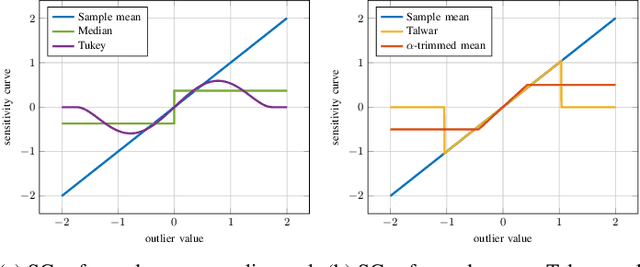
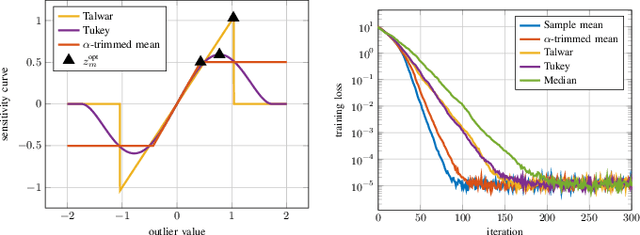
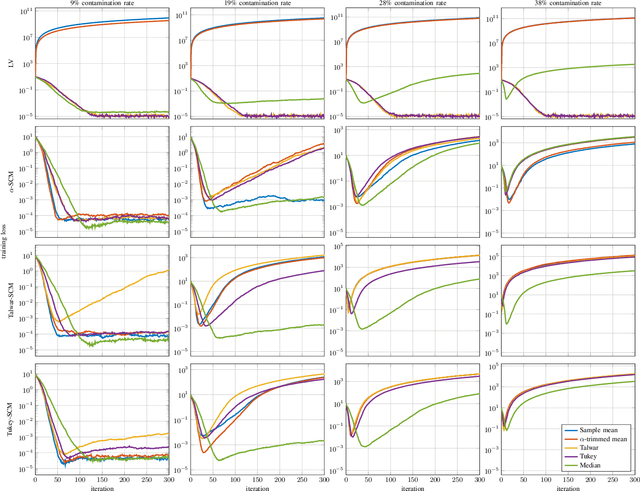
Abstract:Distributed learning paradigms, such as federated or decentralized learning, allow a collection of agents to solve global learning and optimization problems through limited local interactions. Most such strategies rely on a mixture of local adaptation and aggregation steps, either among peers or at a central fusion center. Classically, aggregation in distributed learning is based on averaging, which is statistically efficient, but susceptible to attacks by even a small number of malicious agents. This observation has motivated a number of recent works, which develop robust aggregation schemes by employing robust variations of the mean. We present a new attack based on sensitivity curve maximization (SCM), and demonstrate that it is able to disrupt existing robust aggregation schemes by injecting small, but effective perturbations.
Exact Subspace Diffusion for Decentralized Multitask Learning
Apr 14, 2023

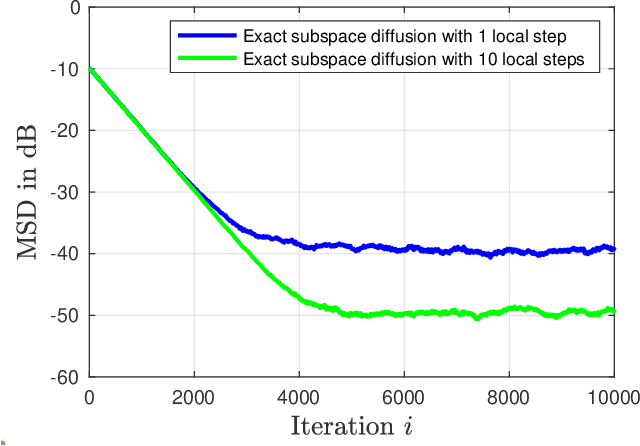
Abstract:Classical paradigms for distributed learning, such as federated or decentralized gradient descent, employ consensus mechanisms to enforce homogeneity among agents. While these strategies have proven effective in i.i.d. scenarios, they can result in significant performance degradation when agents follow heterogeneous objectives or data. Distributed strategies for multitask learning, on the other hand, induce relationships between agents in a more nuanced manner, and encourage collaboration without enforcing consensus. We develop a generalization of the exact diffusion algorithm for subspace constrained multitask learning over networks, and derive an accurate expression for its mean-squared deviation when utilizing noisy gradient approximations. We verify numerically the accuracy of the predicted performance expressions, as well as the improved performance of the proposed approach over alternatives based on approximate projections.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge