Aaron Fainman
Graph-Aware Learning Rates for Decentralized Optimization
Sep 18, 2025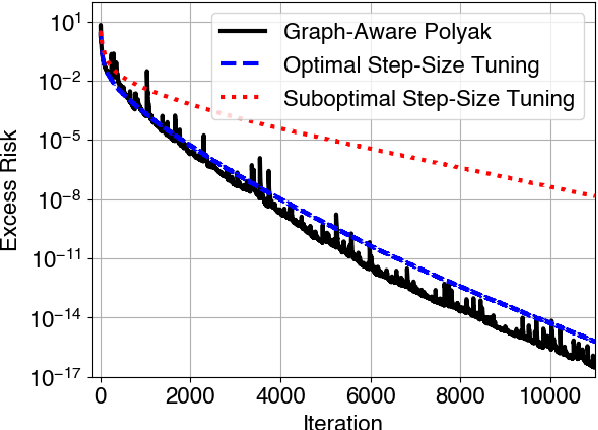
Abstract:We propose an adaptive step-size rule for decentralized optimization. Choosing a step-size that balances convergence and stability is challenging. This is amplified in the decentralized setting as agents observe only local (possibly stochastic) gradients and global information (like smoothness) is unavailable. We derive a step-size rule from first principles. The resulting formulation reduces to the well-known Polyak's rule in the single-agent setting, and is suitable for use with stochastic gradients. The method is parameter free, apart from requiring the optimal objective value, which is readily available in many applications. Numerical simulations demonstrate that the performance is comparable to the optimally fine-tuned step-size.
On the Convergence of Decentralized Stochastic Gradient-Tracking with Finite-Time Consensus
May 29, 2025Abstract:Algorithms for decentralized optimization and learning rely on local optimization steps coupled with combination steps over a graph. Recent works have demonstrated that using a time-varying sequence of matrices that achieve finite-time consensus can improve the communication and iteration complexity of decentralized optimization algorithms based on gradient tracking. In practice, a sequence of matrices satisfying the exact finite-time consensus property may not be available due to imperfect knowledge of the network topology, a limit on the length of the sequence, or numerical instabilities. In this work, we quantify the impact of approximate finite-time consensus sequences on the convergence of a gradient-tracking based decentralized optimization algorithm, clarifying the interplay between accuracy and length of the sequence as well as typical problem parameters such as smoothness and gradient noise.
Decentralized Learning with Approximate Finite-Time Consensus
Jan 14, 2025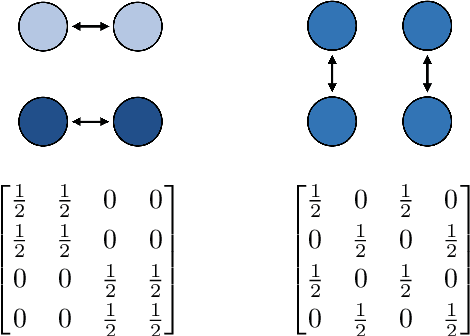
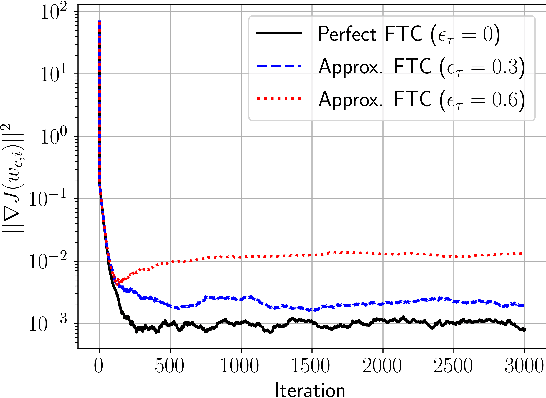
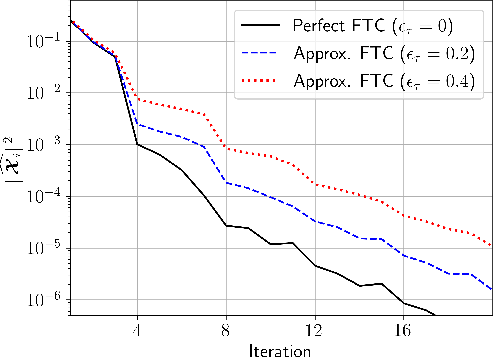
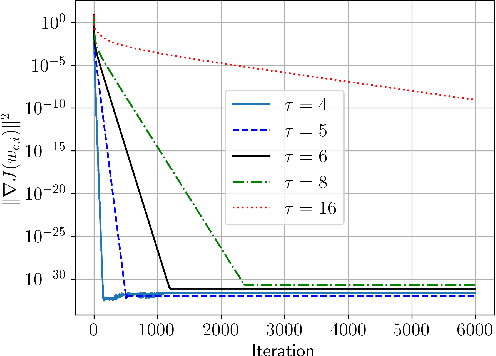
Abstract:The performance of algorithms for decentralized optimization is affected by both the optimization error and the consensus error, the latter of which arises from the variation between agents' local models. Classically, algorithms employ averaging and gradient-tracking mechanisms with constant combination matrices to drive the collection of agents to consensus. Recent works have demonstrated that using sequences of combination matrices that achieve finite-time consensus (FTC) can result in improved communication efficiency or iteration complexity for decentralized optimization. Notably, these studies apply to highly structured networks, where exact finite-time consensus sequences are known exactly and in closed form. In this work we investigate the impact of utilizing approximate FTC matrices in decentralized learning algorithms, and quantify the impact of the approximation error on convergence rate and steady-state performance. Approximate FTC matrices can be inferred for general graphs and do not rely on a particular graph structure or prior knowledge, making the proposed scheme applicable to a broad range of decentralized learning settings.
Deep-Relative-Trust-Based Diffusion for Decentralized Deep Learning
Jan 06, 2025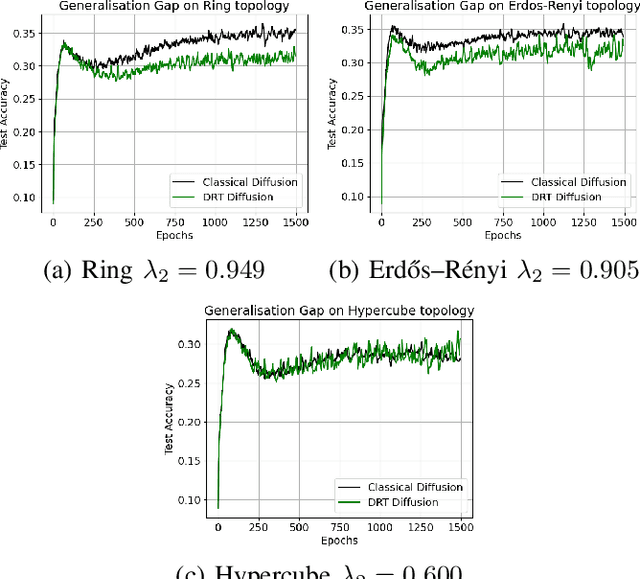
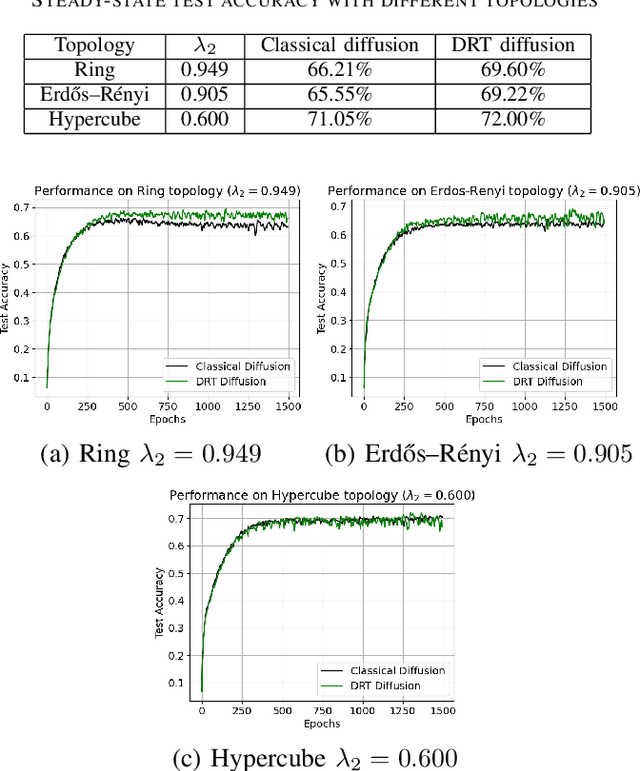
Abstract:Decentralized learning strategies allow a collection of agents to learn efficiently from local data sets without the need for central aggregation or orchestration. Current decentralized learning paradigms typically rely on an averaging mechanism to encourage agreement in the parameter space. We argue that in the context of deep neural networks, which are often over-parameterized, encouraging consensus of the neural network outputs, as opposed to their parameters can be more appropriate. This motivates the development of a new decentralized learning algorithm, termed DRT diffusion, based on deep relative trust (DRT), a recently introduced similarity measure for neural networks. We provide convergence analysis for the proposed strategy, and numerically establish its benefit to generalization, especially with sparse topologies, in an image classification task.
Learned Finite-Time Consensus for Distributed Optimization
Apr 10, 2024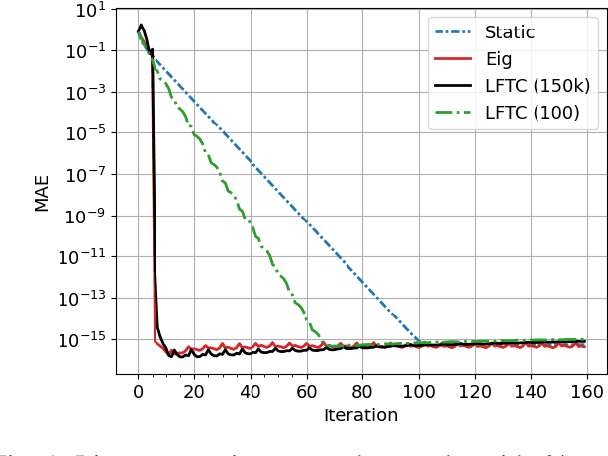
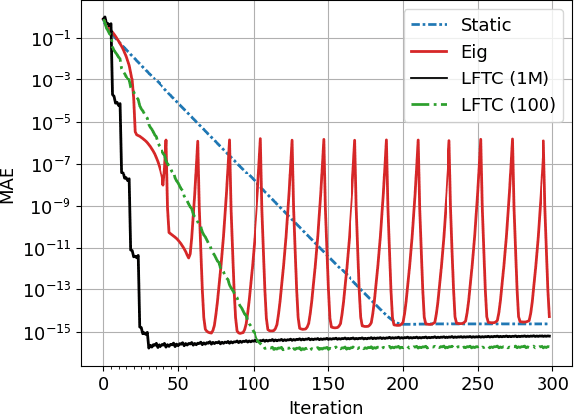
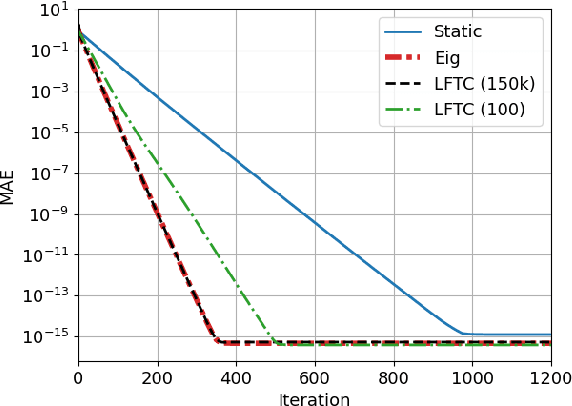
Abstract:Most algorithms for decentralized learning employ a consensus or diffusion mechanism to drive agents to a common solution of a global optimization problem. Generally this takes the form of linear averaging, at a rate of contraction determined by the mixing rate of the underlying network topology. For very sparse graphs this can yield a bottleneck, slowing down the convergence of the learning algorithm. We show that a sequence of matrices achieving finite-time consensus can be learned for unknown graph topologies in a decentralized manner by solving a constrained matrix factorization problem. We demonstrate numerically the benefit of the resulting scheme in both structured and unstructured graphs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge