Differential error feedback for communication-efficient decentralized learning

Communication-constrained algorithms for decentralized learning and optimization rely on local updates coupled with the exchange of compressed signals. In this context, differential quantization is an effective technique to mitigate the negative impact of compression by leveraging correlations between successive iterates. In addition, the use of error feedback, which consists of incorporating the compression error into subsequent steps, is a powerful mechanism to compensate for the bias caused by the compression. Under error feedback, performance guarantees in the literature have so far focused on algorithms employing a fusion center or a special class of contractive compressors that cannot be implemented with a finite number of bits. In this work, we propose a new decentralized communication-efficient learning approach that blends differential quantization with error feedback. The approach is specifically tailored for decentralized learning problems where agents have individual risk functions to minimize subject to subspace constraints that require the minimizers across the network to lie in low-dimensional subspaces. This constrained formulation includes consensus or single-task optimization as special cases, and allows for more general task relatedness models such as multitask smoothness and coupled optimization. We show that, under some general conditions on the compression noise, and for sufficiently small step-sizes $\mu$, the resulting communication-efficient strategy is stable both in terms of mean-square error and average bit rate: by reducing $\mu$, it is possible to keep the estimation errors small (on the order of $\mu$) without increasing indefinitely the bit rate as $\mu\rightarrow 0$. The results establish that, in the small step-size regime and with a finite number of bits, it is possible to attain the performance achievable in the absence of compression.

Exact Subspace Diffusion for Decentralized Multitask Learning

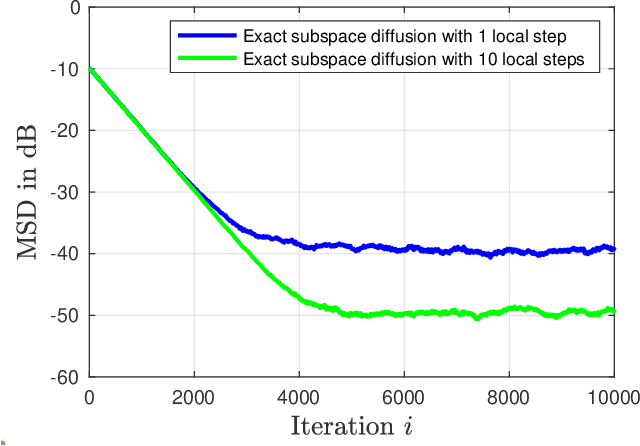
Classical paradigms for distributed learning, such as federated or decentralized gradient descent, employ consensus mechanisms to enforce homogeneity among agents. While these strategies have proven effective in i.i.d. scenarios, they can result in significant performance degradation when agents follow heterogeneous objectives or data. Distributed strategies for multitask learning, on the other hand, induce relationships between agents in a more nuanced manner, and encourage collaboration without enforcing consensus. We develop a generalization of the exact diffusion algorithm for subspace constrained multitask learning over networks, and derive an accurate expression for its mean-squared deviation when utilizing noisy gradient approximations. We verify numerically the accuracy of the predicted performance expressions, as well as the improved performance of the proposed approach over alternatives based on approximate projections.

Quantization for decentralized learning under subspace constraints

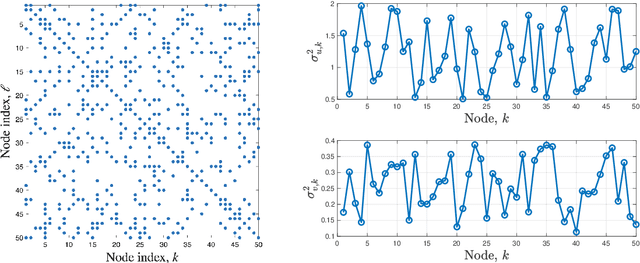
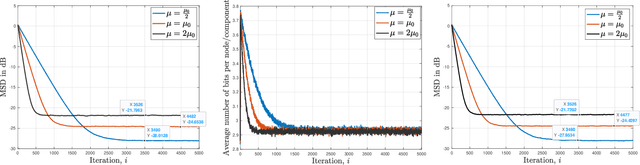
In this paper, we consider decentralized optimization problems where agents have individual cost functions to minimize subject to subspace constraints that require the minimizers across the network to lie in low-dimensional subspaces. This constrained formulation includes consensus or single-task optimization as special cases, and allows for more general task relatedness models such as multitask smoothness and coupled optimization. In order to cope with communication constraints, we propose and study an adaptive decentralized strategy where the agents employ differential randomized quantizers to compress their estimates before communicating with their neighbors. The analysis shows that, under some general conditions on the quantization noise, and for sufficiently small step-sizes $\mu$, the strategy is stable both in terms of mean-square error and average bit rate: by reducing $\mu$, it is possible to keep the estimation errors small (on the order of $\mu$) without increasing indefinitely the bit rate as $\mu\rightarrow 0$. Simulations illustrate the theoretical findings and the effectiveness of the proposed approach, revealing that decentralized learning is achievable at the expense of only a few bits.

Dencentralized learning in the presence of low-rank noise

Observations collected by agents in a network may be unreliable due to observation noise or interference. This paper proposes a distributed algorithm that allows each node to improve the reliability of its own observation by relying solely on local computations and interactions with immediate neighbors, assuming that the field (graph signal) monitored by the network lies in a low-dimensional subspace and that a low-rank noise is present in addition to the usual full-rank noise. While oblique projections can be used to project measurements onto a low-rank subspace along a direction that is oblique to the subspace, the resulting solution is not distributed. Starting from the centralized solution, we propose an algorithm that performs the oblique projection of the overall set of observations onto the signal subspace in an iterative and distributed manner. We then show how the oblique projection framework can be extended to handle distributed learning and adaptation problems over networks.

Multitask learning over graphs

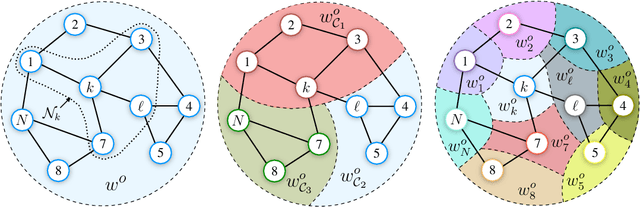
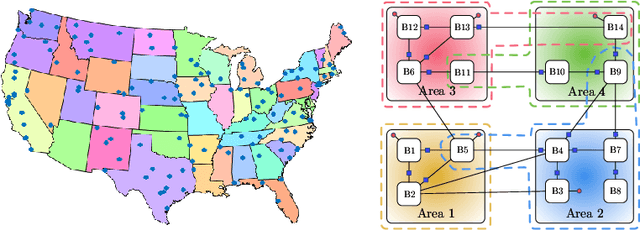
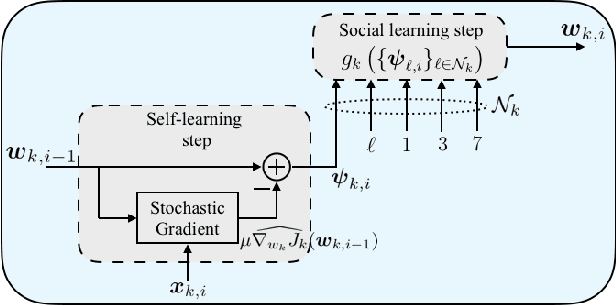
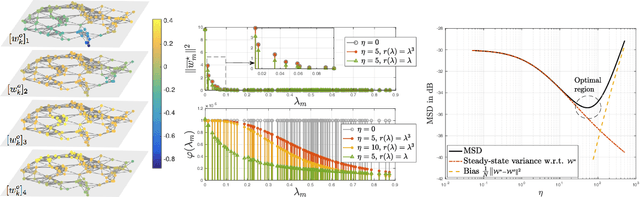
The problem of learning simultaneously several related tasks has received considerable attention in several domains, especially in machine learning with the so-called multitask learning problem or learning to learn problem [1], [2]. Multitask learning is an approach to inductive transfer learning (using what is learned for one problem to assist in another problem) and helps improve generalization performance relative to learning each task separately by using the domain information contained in the training signals of related tasks as an inductive bias. Several strategies have been derived within this community under the assumption that all data are available beforehand at a fusion center. However, recent years have witnessed an increasing ability to collect data in a distributed and streaming manner. This requires the design of new strategies for learning jointly multiple tasks from streaming data over distributed (or networked) systems. This article provides an overview of multitask strategies for learning and adaptation over networks. The working hypothesis for these strategies is that agents are allowed to cooperate with each other in order to learn distinct, though related tasks. The article shows how cooperation steers the network limiting point and how different cooperation rules allow to promote different task relatedness models. It also explains how and when cooperation over multitask networks outperforms non-cooperative strategies.

Network Classifiers With Output Smoothing

This work introduces two strategies for training network classifiers with heterogeneous agents. One strategy promotes global smoothing over the graph and a second strategy promotes local smoothing over neighbourhoods. It is assumed that the feature sizes can vary from one agent to another, with some agents observing insufficient attributes to be able to make reliable decisions on their own. As a result, cooperation with neighbours is necessary. However, due to the fact that the feature dimensions are different across the agents, their classifier dimensions will also be different. This means that cooperation cannot rely on combining the classifier parameters. We instead propose smoothing the outputs of the classifiers, which are the predicted labels. By doing so, the dynamics that describes the evolution of the network classifier becomes more challenging than usual because the classifier parameters end up appearing as part of the regularization term as well. We illustrate performance by means of computer simulations.