Asynchronous Diffusion Learning with Agent Subsampling and Local Updates

In this work, we examine a network of agents operating asynchronously, aiming to discover an ideal global model that suits individual local datasets. Our assumption is that each agent independently chooses when to participate throughout the algorithm and the specific subset of its neighbourhood with which it will cooperate at any given moment. When an agent chooses to take part, it undergoes multiple local updates before conveying its outcomes to the sub-sampled neighbourhood. Under this setup, we prove that the resulting asynchronous diffusion strategy is stable in the mean-square error sense and provide performance guarantees specifically for the federated learning setting. We illustrate the findings with numerical simulations.

Decentralized Adversarial Training over Graphs

The vulnerability of machine learning models to adversarial attacks has been attracting considerable attention in recent years. Most existing studies focus on the behavior of stand-alone single-agent learners. In comparison, this work studies adversarial training over graphs, where individual agents are subjected to perturbations of varied strength levels across space. It is expected that interactions by linked agents, and the heterogeneity of the attack models that are possible over the graph, can help enhance robustness in view of the coordination power of the group. Using a min-max formulation of diffusion learning, we develop a decentralized adversarial training framework for multi-agent systems. We analyze the convergence properties of the proposed scheme for both convex and non-convex environments, and illustrate the enhanced robustness to adversarial attacks.

Multi-Agent Adversarial Training Using Diffusion Learning

This work focuses on adversarial learning over graphs. We propose a general adversarial training framework for multi-agent systems using diffusion learning. We analyze the convergence properties of the proposed scheme for convex optimization problems, and illustrate its enhanced robustness to adversarial attacks.

Enforcing Privacy in Distributed Learning with Performance Guarantees

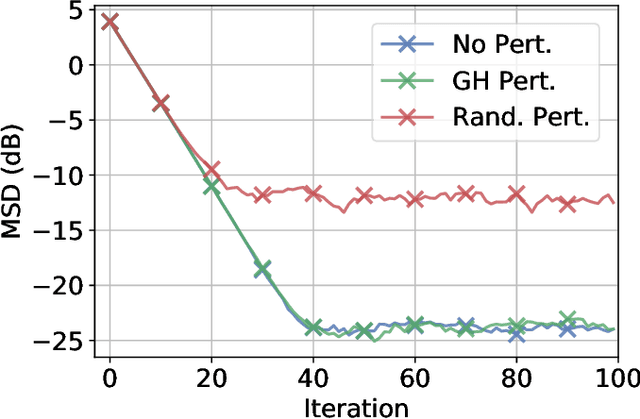
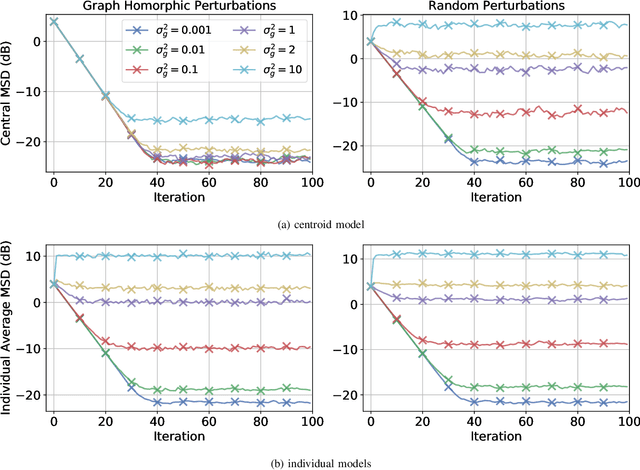
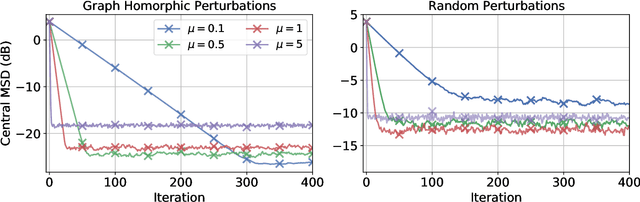
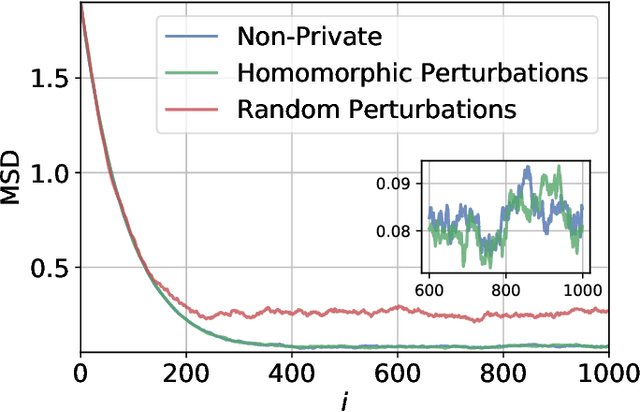
We study the privatization of distributed learning and optimization strategies. We focus on differential privacy schemes and study their effect on performance. We show that the popular additive random perturbation scheme degrades performance because it is not well-tuned to the graph structure. For this reason, we exploit two alternative graph-homomorphic constructions and show that they improve performance while guaranteeing privacy. Moreover, contrary to most earlier studies, the gradient of the risks is not assumed to be bounded (a condition that rarely holds in practice; e.g., quadratic risk). We avoid this condition and still devise a differentially private scheme with high probability. We examine optimization and learning scenarios and illustrate the theoretical findings through simulations.

Local Graph-homomorphic Processing for Privatized Distributed Systems

We study the generation of dependent random numbers in a distributed fashion in order to enable privatized distributed learning by networked agents. We propose a method that we refer to as local graph-homomorphic processing; it relies on the construction of particular noises over the edges to ensure a certain level of differential privacy. We show that the added noise does not affect the performance of the learned model. This is a significant improvement to previous works on differential privacy for distributed algorithms, where the noise was added in a less structured manner without respecting the graph topology and has often led to performance deterioration. We illustrate the theoretical results by considering a linear regression problem over a network of agents.

Privatized Graph Federated Learning

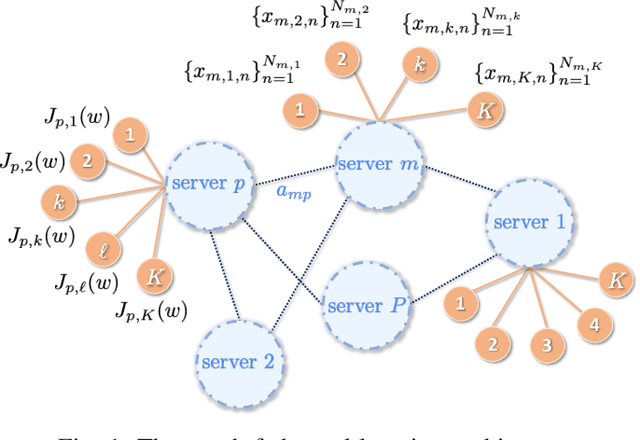
Federated learning is a semi-distributed algorithm, where a server communicates with multiple dispersed clients to learn a global model. The federated architecture is not robust and is sensitive to communication and computational overloads due to its one-master multi-client structure. It can also be subject to privacy attacks targeting personal information on the communication links. In this work, we introduce graph federated learning (GFL), which consists of multiple federated units connected by a graph. We then show how graph homomorphic perturbations can be used to ensure the algorithm is differentially private. We conduct both convergence and privacy theoretical analyses and illustrate performance by means of computer simulations.

A Graph Federated Architecture with Privacy Preserving Learning

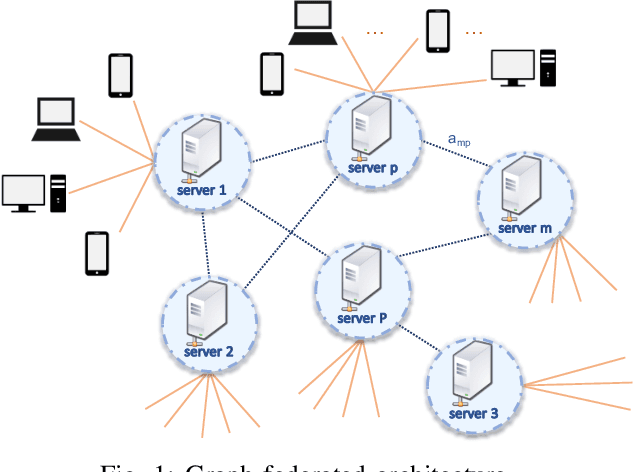
Federated learning involves a central processor that works with multiple agents to find a global model. The process consists of repeatedly exchanging estimates, which results in the diffusion of information pertaining to the local private data. Such a scheme can be inconvenient when dealing with sensitive data, and therefore, there is a need for the privatization of the algorithms. Furthermore, the current architecture of a server connected to multiple clients is highly sensitive to communication failures and computational overloads at the server. Thus in this work, we develop a private multi-server federated learning scheme, which we call graph federated learning. We use cryptographic and differential privacy concepts to privatize the federated learning algorithm that we extend to the graph structure. We study the effect of privatization on the performance of the learning algorithm for general private schemes that can be modeled as additive noise. We show under convexity and Lipschitz conditions, that the privatized process matches the performance of the non-private algorithm, even when we increase the noise variance.

Federated Learning under Importance Sampling

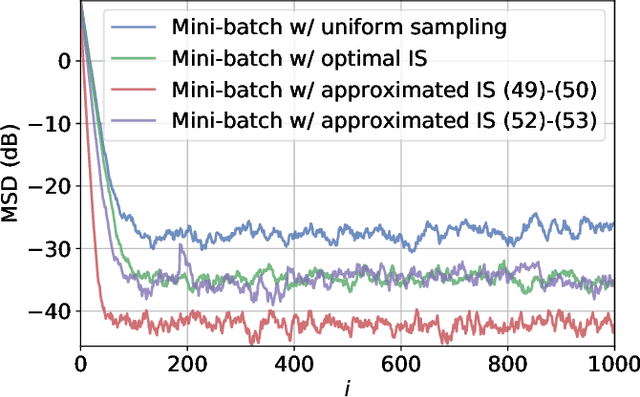
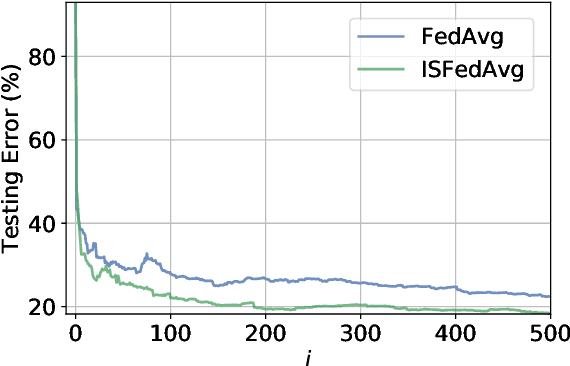
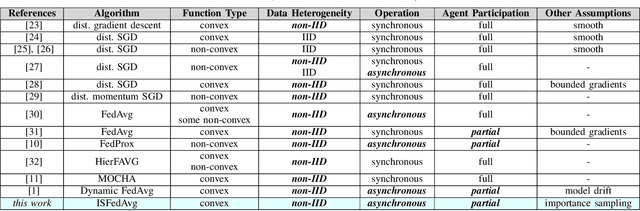
Federated learning encapsulates distributed learning strategies that are managed by a central unit. Since it relies on using a selected number of agents at each iteration, and since each agent, in turn, taps into its local data, it is only natural to study optimal sampling policies for selecting agents and their data in federated learning implementations. Usually, only uniform sampling schemes are used. However, in this work, we examine the effect of importance sampling and devise schemes for sampling agents and data non-uniformly guided by a performance measure. We find that in schemes involving sampling without replacement, the performance of the resulting architecture is controlled by two factors related to data variability at each agent, and model variability across agents. We illustrate the theoretical findings with experiments on simulated and real data and show the improvement in performance that results from the proposed strategies.

Second-Order Guarantees in Federated Learning

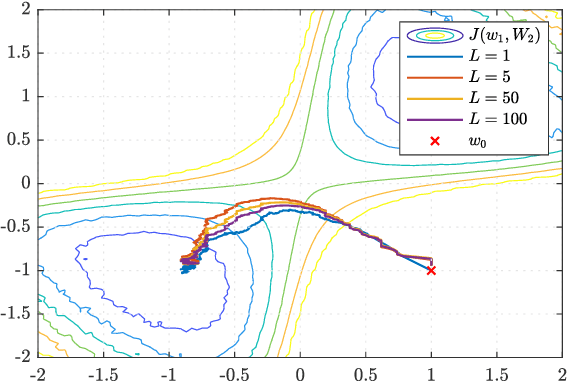
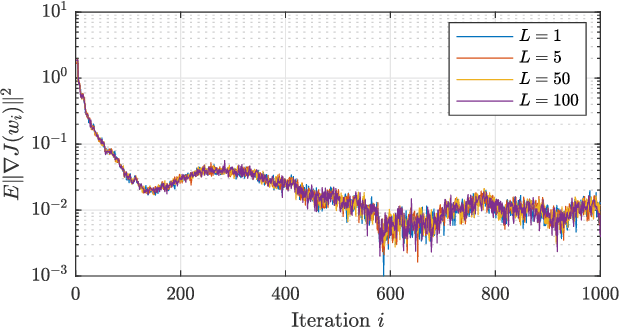
Federated learning is a useful framework for centralized learning from distributed data under practical considerations of heterogeneity, asynchrony, and privacy. Federated architectures are frequently deployed in deep learning settings, which generally give rise to non-convex optimization problems. Nevertheless, most existing analysis are either limited to convex loss functions, or only establish first-order stationarity, despite the fact that saddle-points, which are first-order stationary, are known to pose bottlenecks in deep learning. We draw on recent results on the second-order optimality of stochastic gradient algorithms in centralized and decentralized settings, and establish second-order guarantees for a class of federated learning algorithms.

Optimal Importance Sampling for Federated Learning

Federated learning involves a mixture of centralized and decentralized processing tasks, where a server regularly selects a sample of the agents and these in turn sample their local data to compute stochastic gradients for their learning updates. This process runs continually. The sampling of both agents and data is generally uniform; however, in this work we consider non-uniform sampling. We derive optimal importance sampling strategies for both agent and data selection and show that non-uniform sampling without replacement improves the performance of the original FedAvg algorithm. We run experiments on a regression and classification problem to illustrate the theoretical results.