Multitask learning over graphs

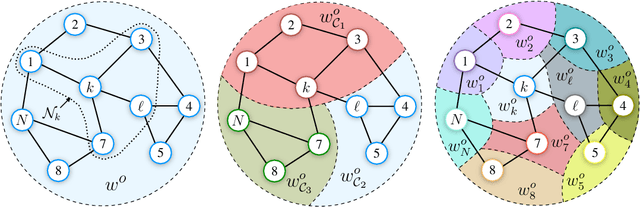
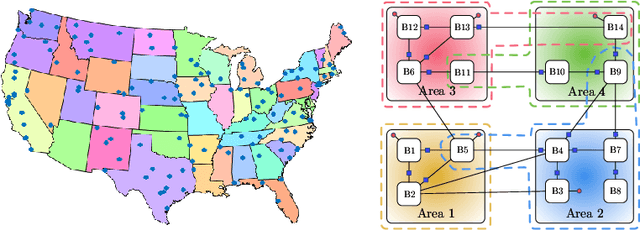
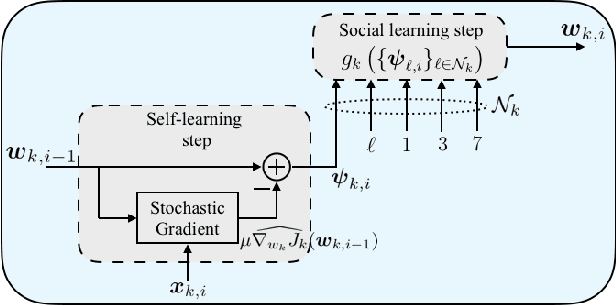
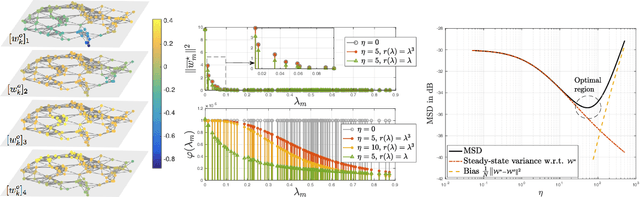
The problem of learning simultaneously several related tasks has received considerable attention in several domains, especially in machine learning with the so-called multitask learning problem or learning to learn problem [1], [2]. Multitask learning is an approach to inductive transfer learning (using what is learned for one problem to assist in another problem) and helps improve generalization performance relative to learning each task separately by using the domain information contained in the training signals of related tasks as an inductive bias. Several strategies have been derived within this community under the assumption that all data are available beforehand at a fusion center. However, recent years have witnessed an increasing ability to collect data in a distributed and streaming manner. This requires the design of new strategies for learning jointly multiple tasks from streaming data over distributed (or networked) systems. This article provides an overview of multitask strategies for learning and adaptation over networks. The working hypothesis for these strategies is that agents are allowed to cooperate with each other in order to learn distinct, though related tasks. The article shows how cooperation steers the network limiting point and how different cooperation rules allow to promote different task relatedness models. It also explains how and when cooperation over multitask networks outperforms non-cooperative strategies.

Decentralized Online Learning with Kernels

We consider multi-agent stochastic optimization problems over reproducing kernel Hilbert spaces (RKHS). In this setting, a network of interconnected agents aims to learn decision functions, i.e., nonlinear statistical models, that are optimal in terms of a global convex functional that aggregates data across the network, with only access to locally and sequentially observed samples. We propose solving this problem by allowing each agent to learn a local regression function while enforcing consensus constraints. We use a penalized variant of functional stochastic gradient descent operating simultaneously with low-dimensional subspace projections. These subspaces are constructed greedily by applying orthogonal matching pursuit to the sequence of kernel dictionaries and weights. By tuning the projection-induced bias, we propose an algorithm that allows for each individual agent to learn, based upon its locally observed data stream and message passing with its neighbors only, a regression function that is close to the globally optimal regression function. That is, we establish that with constant step-size selections agents' functions converge to a neighborhood of the globally optimal one while satisfying the consensus constraints as the penalty parameter is increased. Moreover, the complexity of the learned regression functions is guaranteed to remain finite. On both multi-class kernel logistic regression and multi-class kernel support vector classification with data generated from class-dependent Gaussian mixture models, we observe stable function estimation and state of the art performance for distributed online multi-class classification. Experiments on the Brodatz textures further substantiate the empirical validity of this approach.

A stochastic behavior analysis of stochastic restricted-gradient descent algorithm in reproducing kernel Hilbert spaces

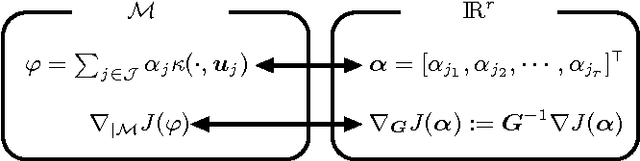
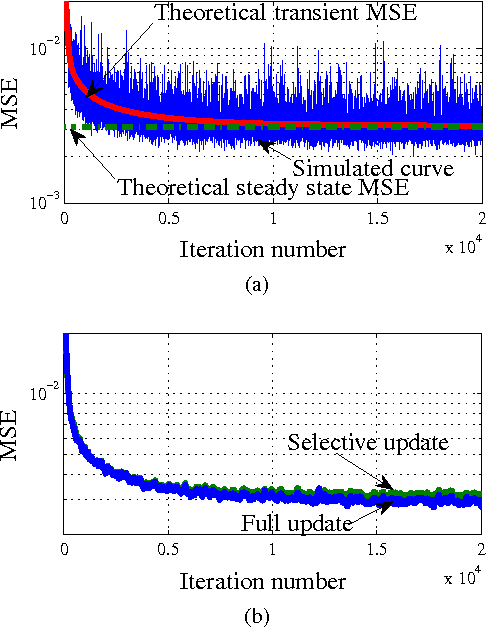
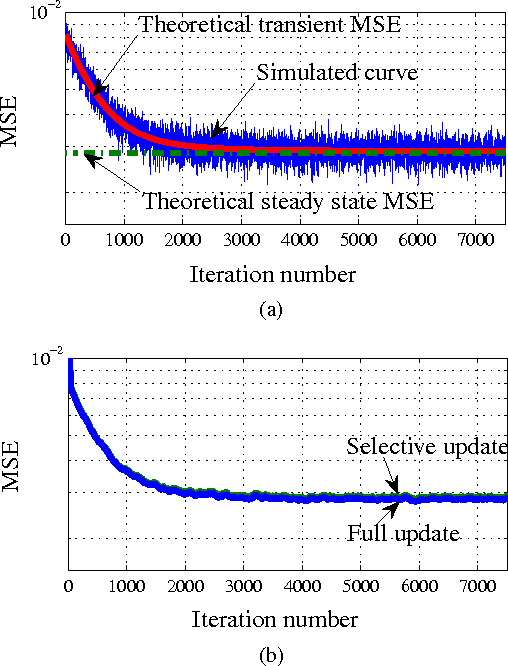
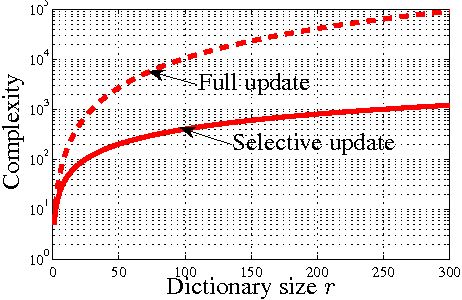
This paper presents a stochastic behavior analysis of a kernel-based stochastic restricted-gradient descent method. The restricted gradient gives a steepest ascent direction within the so-called dictionary subspace. The analysis provides the transient and steady state performance in the mean squared error criterion. It also includes stability conditions in the mean and mean-square sense. The present study is based on the analysis of the kernel normalized least mean square (KNLMS) algorithm initially proposed by Chen et al. Simulation results validate the analysis.