A Graph Signal Processing Perspective of Network Multiple Hypothesis Testing with False Discovery Rate Control

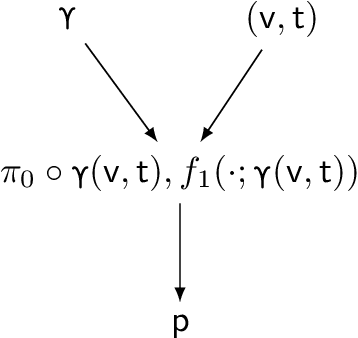
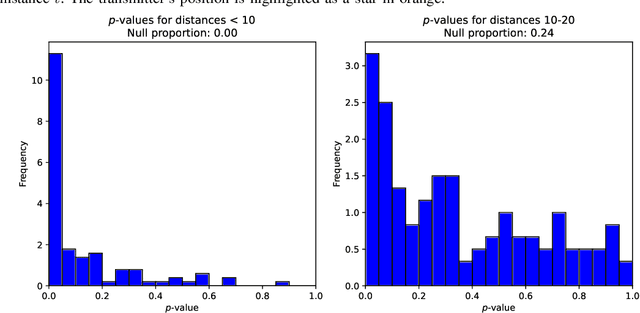
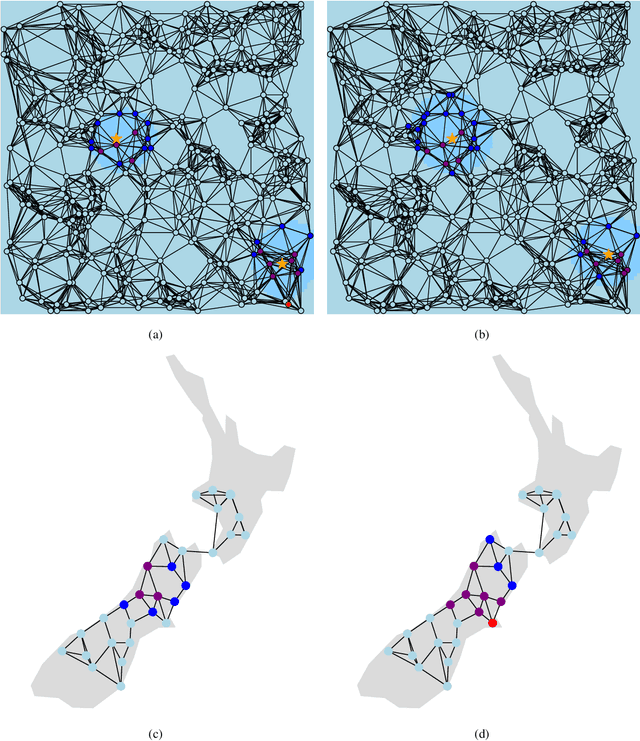
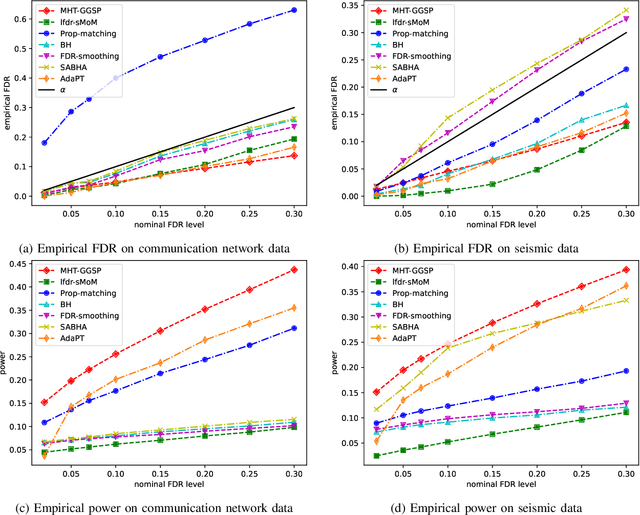
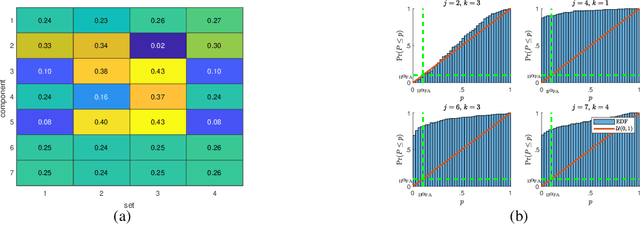
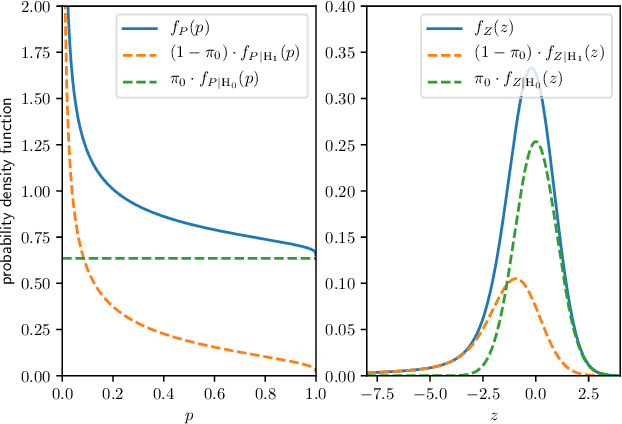
We consider a multiple hypothesis testing problem in a sensor network over the joint spatial-time domain. The sensor network is modeled as a graph, with each vertex representing a sensor and a signal over time associated with each vertex. We assume a hypothesis test and an associated p-value for every sample point in the joint spatial-time domain. Our goal is to determine which points have true alternative hypotheses. By parameterizing the unknown alternative distribution of $p$-values and the prior probabilities of hypotheses being null with a bandlimited generalized graph signal, we can obtain consistent estimates for them. Consequently, we also obtain an estimate of the local false discovery rates (lfdr). We prove that by using a step-up procedure on the estimated lfdr, we can achieve asymptotic false discovery rate control at a pre-determined level. Numerical experiments validate the effectiveness of our approach compared to existing methods.

Identifying the Complete Correlation Structure in Large-Scale High-Dimensional Data Sets with Local False Discovery Rates

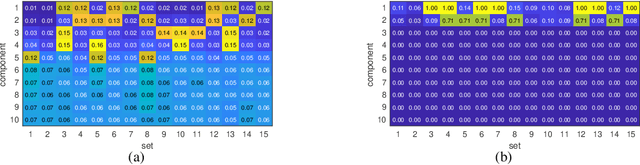
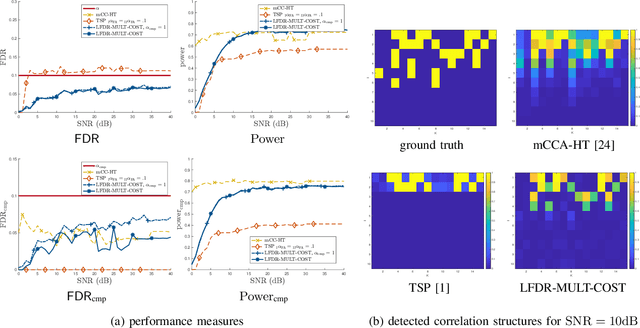
The identification of the dependent components in multiple data sets is a fundamental problem in many practical applications. The challenge in these applications is that often the data sets are high-dimensional with few observations or available samples and contain latent components with unknown probability distributions. A novel mathematical formulation of this problem is proposed, which enables the inference of the underlying correlation structure with strict false positive control. In particular, the false discovery rate is controlled at a pre-defined threshold on two levels simultaneously. The deployed test statistics originate in the sample coherence matrix. The required probability models are learned from the data using the bootstrap. Local false discovery rates are used to solve the multiple hypothesis testing problem. Compared to the existing techniques in the literature, the developed technique does not assume an a priori correlation structure and work well when the number of data sets is large while the number of observations is small. In addition, it can handle the presence of distributional uncertainties, heavy-tailed noise, and outliers.

Multiple Hypothesis Testing Framework for Spatial Signals

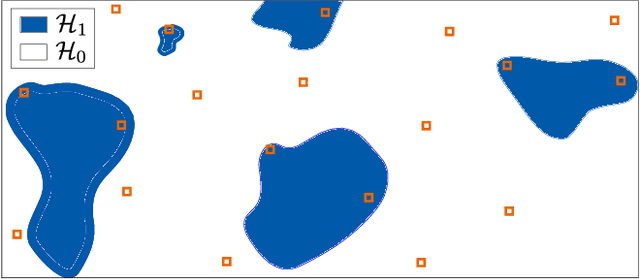
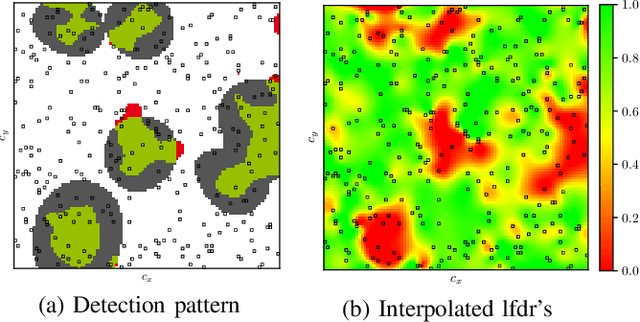
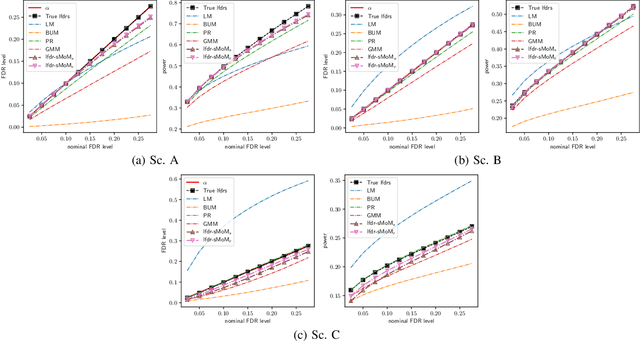
The problem of identifying regions of spatially interesting, different or adversarial behavior is inherent to many practical applications involving distributed multisensor systems. In this work, we develop a general framework stemming from multiple hypothesis testing to identify such regions. A discrete spatial grid is assumed for the monitored environment. The spatial grid points associated with different hypotheses are identified while controlling the false discovery rate at a pre-specified level. Measurements are acquired using a large-scale sensor network. We propose a novel, data-driven method to estimate local false discovery rates based on the spectral method of moments. Our method is agnostic to specific spatial propagation models of the underlying physical phenomenon. It relies on a broadly applicable density model for local summary statistics. In between sensors, locations are assigned to regions associated with different hypotheses based on interpolated local false discovery rates. The benefits of our method are illustrated by applications to spatially propagating radio waves.