Xingchao Jian
Conformal Prediction for Multi-Source Detection on a Network
Nov 12, 2025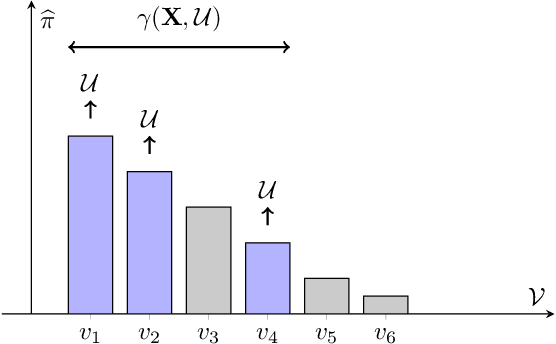
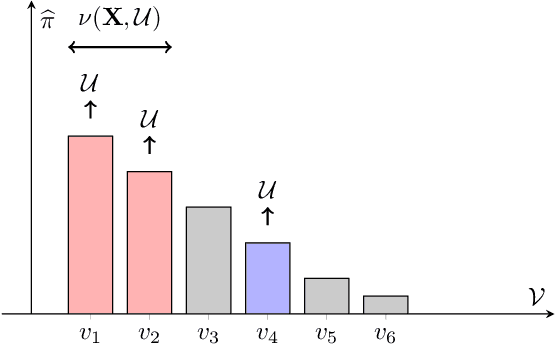
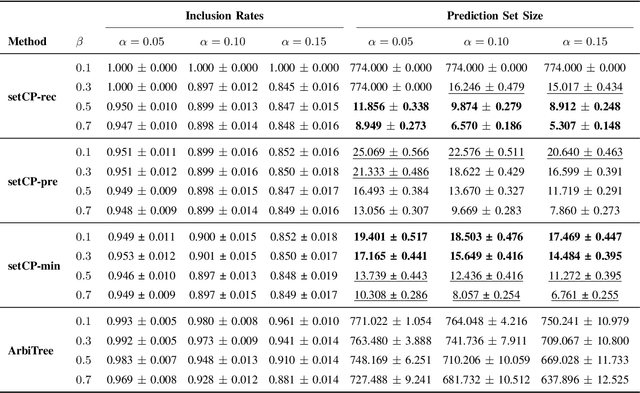
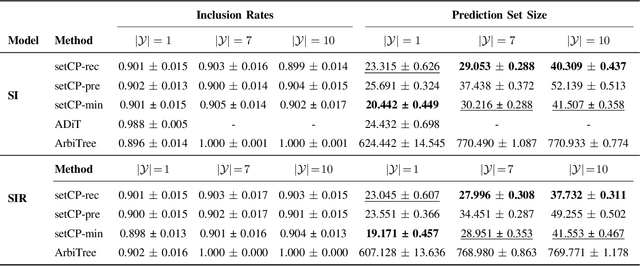
Abstract:Detecting the origin of information or infection spread in networks is a fundamental challenge with applications in misinformation tracking, epidemiology, and beyond. We study the multi-source detection problem: given snapshot observations of node infection status on a graph, estimate the set of source nodes that initiated the propagation. Existing methods either lack statistical guarantees or are limited to specific diffusion models and assumptions. We propose a novel conformal prediction framework that provides statistically valid recall guarantees for source set detection, independent of the underlying diffusion process or data distribution. Our approach introduces principled score functions to quantify the alignment between predicted probabilities and true sources, and leverages a calibration set to construct prediction sets with user-specified recall and coverage levels. The method is applicable to both single- and multi-source scenarios, supports general network diffusion dynamics, and is computationally efficient for large graphs. Empirical results demonstrate that our method achieves rigorous coverage with competitive accuracy, outperforming existing baselines in both reliability and scalability.The code is available online.
Simple Graph Contrastive Learning via Fractional-order Neural Diffusion Networks
Apr 24, 2025Abstract:Graph Contrastive Learning (GCL) has recently made progress as an unsupervised graph representation learning paradigm. GCL approaches can be categorized into augmentation-based and augmentation-free methods. The former relies on complex data augmentations, while the latter depends on encoders that can generate distinct views of the same input. Both approaches may require negative samples for training. In this paper, we introduce a novel augmentation-free GCL framework based on graph neural diffusion models. Specifically, we utilize learnable encoders governed by Fractional Differential Equations (FDE). Each FDE is characterized by an order parameter of the differential operator. We demonstrate that varying these parameters allows us to produce learnable encoders that generate diverse views, capturing either local or global information, for contrastive learning. Our model does not require negative samples for training and is applicable to both homophilic and heterophilic datasets. We demonstrate its effectiveness across various datasets, achieving state-of-the-art performance.
Generalized Graph Signal Reconstruction via the Uncertainty Principle
Sep 06, 2024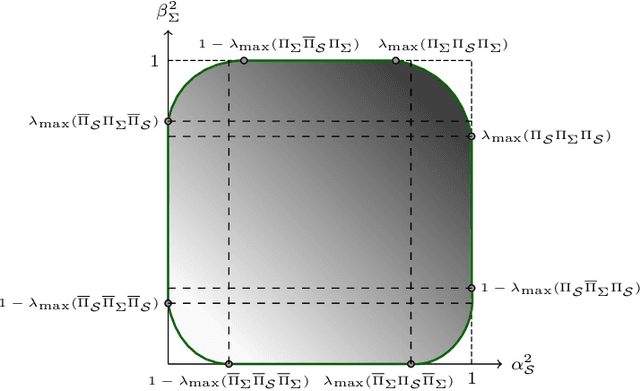
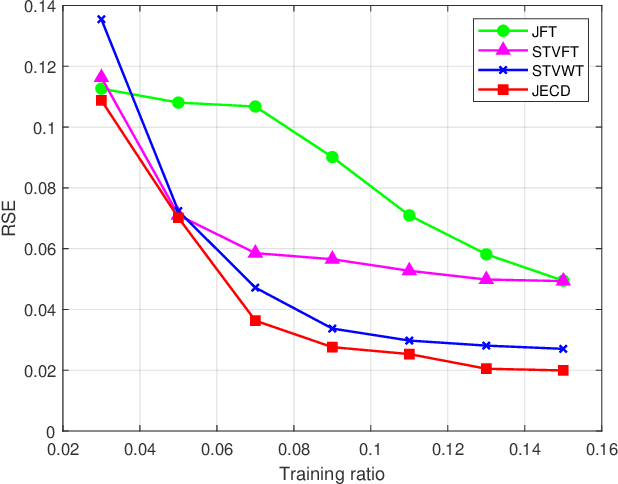
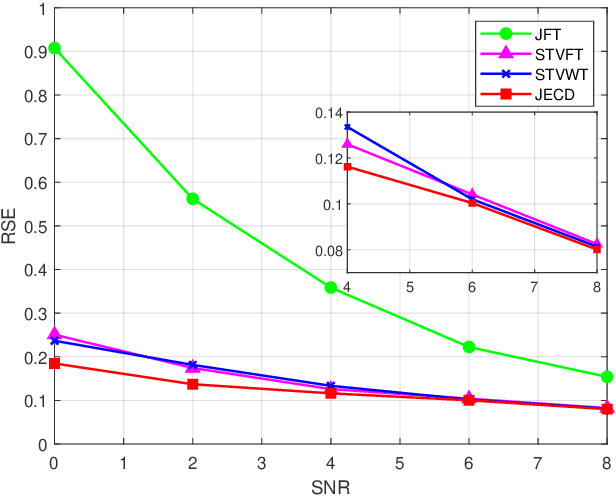
Abstract:We introduce a novel uncertainty principle for generalized graph signals that extends classical time-frequency and graph uncertainty principles into a unified framework. By defining joint vertex-time and spectral-frequency spreads, we quantify signal localization across these domains, revealing a trade-off between them. This framework allows us to identify a class of signals with maximal energy concentration in both domains, forming the fundamental atoms for a new joint vertex-time dictionary. This dictionary enhances signal reconstruction under practical constraints, such as incomplete or intermittent data, commonly encountered in sensor and social networks. Numerical experiments on real-world datasets demonstrate the effectiveness of the proposed approach, showing improved reconstruction accuracy and noise robustness compared to existing methods.
A Graph Signal Processing Perspective of Network Multiple Hypothesis Testing with False Discovery Rate Control
Aug 06, 2024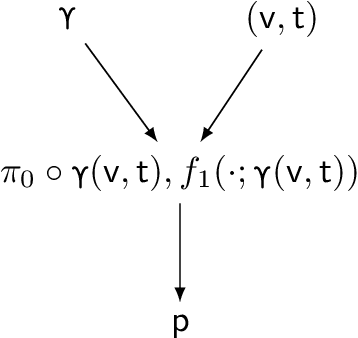
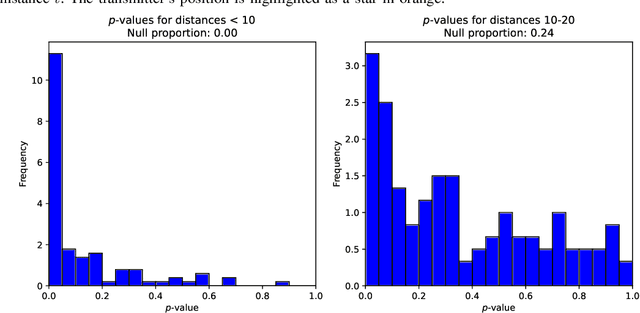
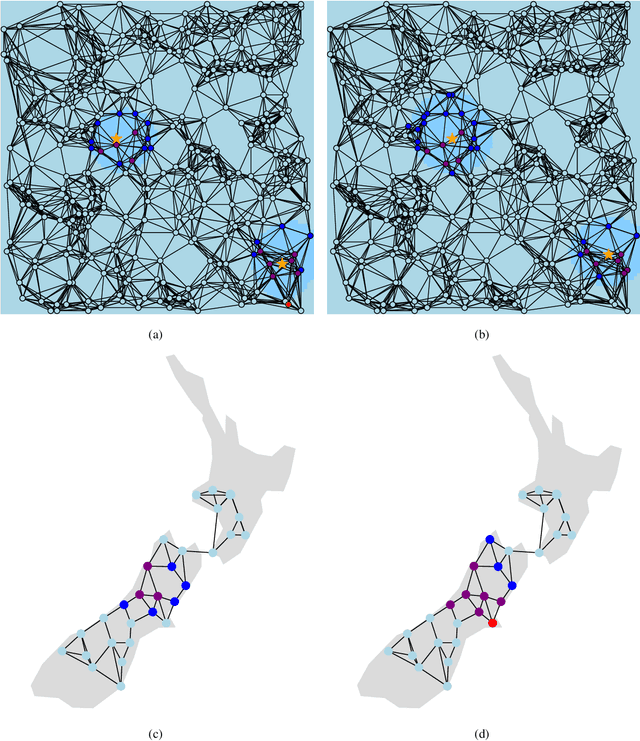
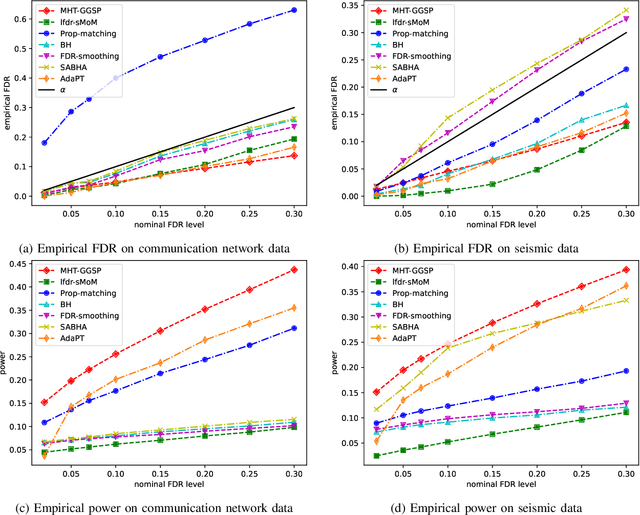
Abstract:We consider a multiple hypothesis testing problem in a sensor network over the joint spatial-time domain. The sensor network is modeled as a graph, with each vertex representing a sensor and a signal over time associated with each vertex. We assume a hypothesis test and an associated p-value for every sample point in the joint spatial-time domain. Our goal is to determine which points have true alternative hypotheses. By parameterizing the unknown alternative distribution of $p$-values and the prior probabilities of hypotheses being null with a bandlimited generalized graph signal, we can obtain consistent estimates for them. Consequently, we also obtain an estimate of the local false discovery rates (lfdr). We prove that by using a step-up procedure on the estimated lfdr, we can achieve asymptotic false discovery rate control at a pre-determined level. Numerical experiments validate the effectiveness of our approach compared to existing methods.
PosDiffNet: Positional Neural Diffusion for Point Cloud Registration in a Large Field of View with Perturbations
Jan 06, 2024Abstract:Point cloud registration is a crucial technique in 3D computer vision with a wide range of applications. However, this task can be challenging, particularly in large fields of view with dynamic objects, environmental noise, or other perturbations. To address this challenge, we propose a model called PosDiffNet. Our approach performs hierarchical registration based on window-level, patch-level, and point-level correspondence. We leverage a graph neural partial differential equation (PDE) based on Beltrami flow to obtain high-dimensional features and position embeddings for point clouds. We incorporate position embeddings into a Transformer module based on a neural ordinary differential equation (ODE) to efficiently represent patches within points. We employ the multi-level correspondence derived from the high feature similarity scores to facilitate alignment between point clouds. Subsequently, we use registration methods such as SVD-based algorithms to predict the transformation using corresponding point pairs. We evaluate PosDiffNet on several 3D point cloud datasets, verifying that it achieves state-of-the-art (SOTA) performance for point cloud registration in large fields of view with perturbations. The implementation code of experiments is available at https://github.com/AI-IT-AVs/PosDiffNet.
Sparse graph sequences, generalized graphons and signal processing
Dec 21, 2023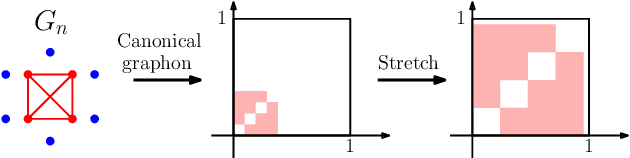
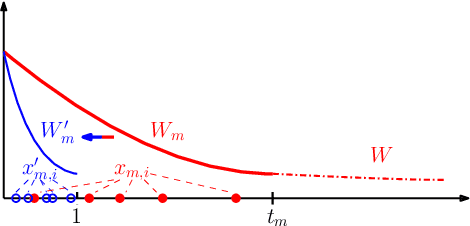
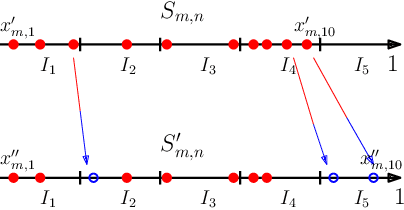
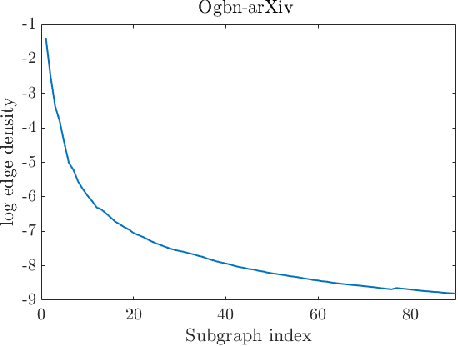
Abstract:Graphons are limit objects of sequences of graphs, used to analyze the behavior of large graphs. Recently, graphon signal processing has been developed to study large graphs from the signal processing perspective. However, it has the shortcoming that any sparse sequence of graphs always converges to the zero graphon, and the resulting signal processing theory is trivial. In this paper, we propose a signal processing framework based on the generalized graphon theory. The main ingredient is to use the stretched cut distance to compare these graphons. We focus on sampling graph sequences from generalized graphons, and discuss convergence results of associated operators, spectrum as well as signals. Though the paper is theoretical, we also discuss what the theory implies for real large networks.
DistilVPR: Cross-Modal Knowledge Distillation for Visual Place Recognition
Dec 17, 2023Abstract:The utilization of multi-modal sensor data in visual place recognition (VPR) has demonstrated enhanced performance compared to single-modal counterparts. Nonetheless, integrating additional sensors comes with elevated costs and may not be feasible for systems that demand lightweight operation, thereby impacting the practical deployment of VPR. To address this issue, we resort to knowledge distillation, which empowers single-modal students to learn from cross-modal teachers without introducing additional sensors during inference. Despite the notable advancements achieved by current distillation approaches, the exploration of feature relationships remains an under-explored area. In order to tackle the challenge of cross-modal distillation in VPR, we present DistilVPR, a novel distillation pipeline for VPR. We propose leveraging feature relationships from multiple agents, including self-agents and cross-agents for teacher and student neural networks. Furthermore, we integrate various manifolds, characterized by different space curvatures for exploring feature relationships. This approach enhances the diversity of feature relationships, including Euclidean, spherical, and hyperbolic relationship modules, thereby enhancing the overall representational capacity. The experiments demonstrate that our proposed pipeline achieves state-of-the-art performance compared to other distillation baselines. We also conduct necessary ablation studies to show design effectiveness. The code is released at: https://github.com/sijieaaa/DistilVPR
Comments on "Graphon Signal Processing''
Oct 23, 2023Abstract:This correspondence points out a technical error in Proposition 4 of the paper [1]. Because of this error, the proofs of Lemma 3, Theorem 1, Theorem 3, Proposition 2, and Theorem 4 in that paper are no longer valid. We provide counterexamples to Proposition 4 and discuss where the flaw in its proof lies. We also provide numerical evidence indicating that Lemma 3, Theorem 1, and Proposition 2 are likely to be false. Since the proof of Theorem 4 depends on the validity of Proposition 4, we propose an amendment to the statement of Theorem 4 of the paper using convergence in operator norm and prove this rigorously. In addition, we also provide a construction that guarantees convergence in the sense of Proposition 4.
Frequency Convergence of Complexon Shift Operators (Extended Version)
Sep 15, 2023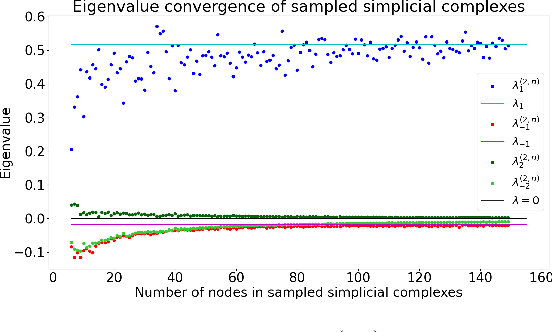
Abstract:Topological Signal Processing (TSP) utilizes simplicial complexes to model structures with higher order than vertices and edges. In this paper, we study the transferability of TSP via a generalized higher-order version of graphon, known as complexon. We recall the notion of a complexon as the limit of a simplicial complex sequence. Inspired by the integral operator form of graphon shift operators, we construct a marginal complexon and complexon shift operator (CSO) according to components of all possible dimensions from the complexon. We investigate the CSO's eigenvalues and eigenvectors, and relate them to a new family of weighted adjacency matrices. We prove that when a simplicial complex sequence converges to a complexon, the eigenvalues of the corresponding CSOs converge to that of the limit complexon. This conclusion is further verified by a numerical experiment. These results hint at learning transferability on large simplicial complexes or simplicial complex sequences, which generalize the graphon signal processing framework.
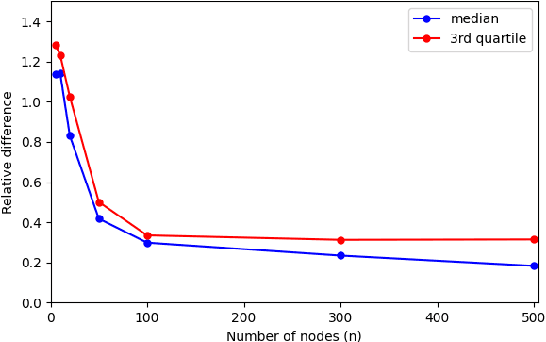
Generalized Graphon Process: Convergence of Graph Frequencies in Stretched Cut Distance
Sep 11, 2023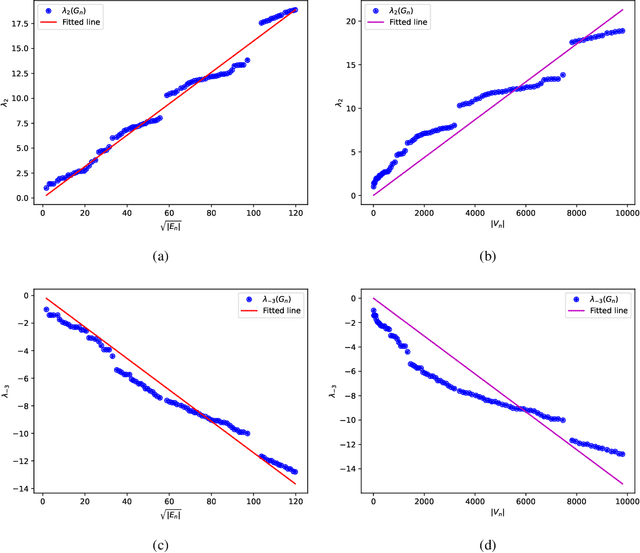
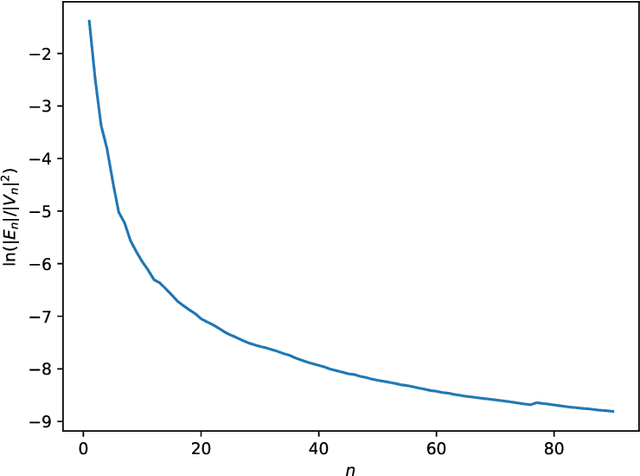
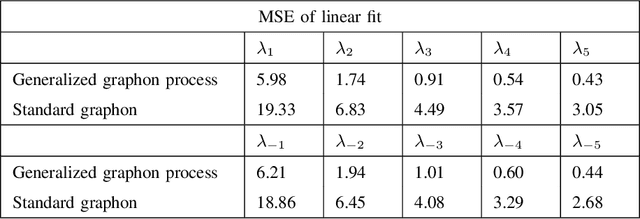
Abstract:Graphons have traditionally served as limit objects for dense graph sequences, with the cut distance serving as the metric for convergence. However, sparse graph sequences converge to the trivial graphon under the conventional definition of cut distance, which make this framework inadequate for many practical applications. In this paper, we utilize the concepts of generalized graphons and stretched cut distance to describe the convergence of sparse graph sequences. Specifically, we consider a random graph process generated from a generalized graphon. This random graph process converges to the generalized graphon in stretched cut distance. We use this random graph process to model the growing sparse graph, and prove the convergence of the adjacency matrices' eigenvalues. We supplement our findings with experimental validation. Our results indicate the possibility of transfer learning between sparse graphs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge