Efficient Training of Neural Fractional-Order Differential Equation via Adjoint Backpropagation

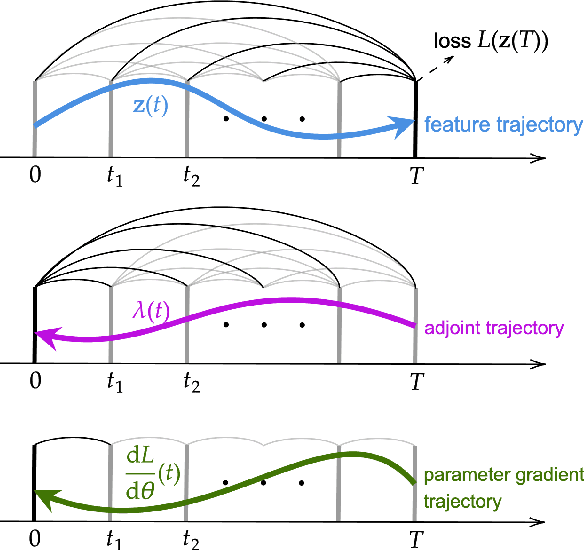
Fractional-order differential equations (FDEs) enhance traditional differential equations by extending the order of differential operators from integers to real numbers, offering greater flexibility in modeling complex dynamical systems with nonlocal characteristics. Recent progress at the intersection of FDEs and deep learning has catalyzed a new wave of innovative models, demonstrating the potential to address challenges such as graph representation learning. However, training neural FDEs has primarily relied on direct differentiation through forward-pass operations in FDE numerical solvers, leading to increased memory usage and computational complexity, particularly in large-scale applications. To address these challenges, we propose a scalable adjoint backpropagation method for training neural FDEs by solving an augmented FDE backward in time, which substantially reduces memory requirements. This approach provides a practical neural FDE toolbox and holds considerable promise for diverse applications. We demonstrate the effectiveness of our method in several tasks, achieving performance comparable to baseline models while significantly reducing computational overhead.

Neural Variable-Order Fractional Differential Equation Networks

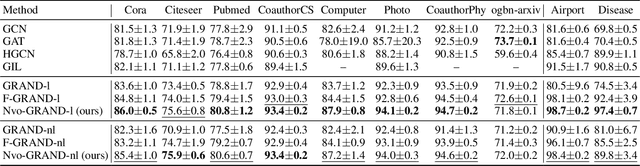
Neural differential equation models have garnered significant attention in recent years for their effectiveness in machine learning applications.Among these, fractional differential equations (FDEs) have emerged as a promising tool due to their ability to capture memory-dependent dynamics, which are often challenging to model with traditional integer-order approaches.While existing models have primarily focused on constant-order fractional derivatives, variable-order fractional operators offer a more flexible and expressive framework for modeling complex memory patterns. In this work, we introduce the Neural Variable-Order Fractional Differential Equation network (NvoFDE), a novel neural network framework that integrates variable-order fractional derivatives with learnable neural networks.Our framework allows for the modeling of adaptive derivative orders dependent on hidden features, capturing more complex feature-updating dynamics and providing enhanced flexibility. We conduct extensive experiments across multiple graph datasets to validate the effectiveness of our approach.Our results demonstrate that NvoFDE outperforms traditional constant-order fractional and integer models across a range of tasks, showcasing its superior adaptability and performance.

Distributed-Order Fractional Graph Operating Network

We introduce the Distributed-order fRActional Graph Operating Network (DRAGON), a novel continuous Graph Neural Network (GNN) framework that incorporates distributed-order fractional calculus. Unlike traditional continuous GNNs that utilize integer-order or single fractional-order differential equations, DRAGON uses a learnable probability distribution over a range of real numbers for the derivative orders. By allowing a flexible and learnable superposition of multiple derivative orders, our framework captures complex graph feature updating dynamics beyond the reach of conventional models. We provide a comprehensive interpretation of our framework's capability to capture intricate dynamics through the lens of a non-Markovian graph random walk with node feature updating driven by an anomalous diffusion process over the graph. Furthermore, to highlight the versatility of the DRAGON framework, we conduct empirical evaluations across a range of graph learning tasks. The results consistently demonstrate superior performance when compared to traditional continuous GNN models. The implementation code is available at \url{https://github.com/zknus/NeurIPS-2024-DRAGON}.

PRFusion: Toward Effective and Robust Multi-Modal Place Recognition with Image and Point Cloud Fusion

Place recognition plays a crucial role in the fields of robotics and computer vision, finding applications in areas such as autonomous driving, mapping, and localization. Place recognition identifies a place using query sensor data and a known database. One of the main challenges is to develop a model that can deliver accurate results while being robust to environmental variations. We propose two multi-modal place recognition models, namely PRFusion and PRFusion++. PRFusion utilizes global fusion with manifold metric attention, enabling effective interaction between features without requiring camera-LiDAR extrinsic calibrations. In contrast, PRFusion++ assumes the availability of extrinsic calibrations and leverages pixel-point correspondences to enhance feature learning on local windows. Additionally, both models incorporate neural diffusion layers, which enable reliable operation even in challenging environments. We verify the state-of-the-art performance of both models on three large-scale benchmarks. Notably, they outperform existing models by a substantial margin of +3.0 AR@1 on the demanding Boreas dataset. Furthermore, we conduct ablation studies to validate the effectiveness of our proposed methods. The codes are available at: https://github.com/sijieaaa/PRFusion

Unleashing the Potential of Fractional Calculus in Graph Neural Networks with FROND

We introduce the FRactional-Order graph Neural Dynamical network (FROND), a new continuous graph neural network (GNN) framework. Unlike traditional continuous GNNs that rely on integer-order differential equations, FROND employs the Caputo fractional derivative to leverage the non-local properties of fractional calculus. This approach enables the capture of long-term dependencies in feature updates, moving beyond the Markovian update mechanisms in conventional integer-order models and offering enhanced capabilities in graph representation learning. We offer an interpretation of the node feature updating process in FROND from a non-Markovian random walk perspective when the feature updating is particularly governed by a diffusion process. We demonstrate analytically that oversmoothing can be mitigated in this setting. Experimentally, we validate the FROND framework by comparing the fractional adaptations of various established integer-order continuous GNNs, demonstrating their consistently improved performance and underscoring the framework's potential as an effective extension to enhance traditional continuous GNNs. The code is available at \url{https://github.com/zknus/ICLR2024-FROND}.

PointDifformer: Robust Point Cloud Registration With Neural Diffusion and Transformer

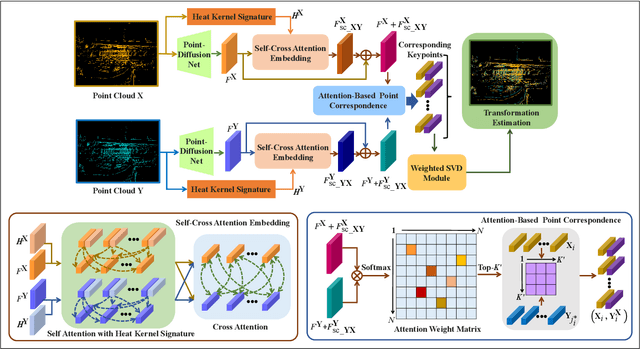
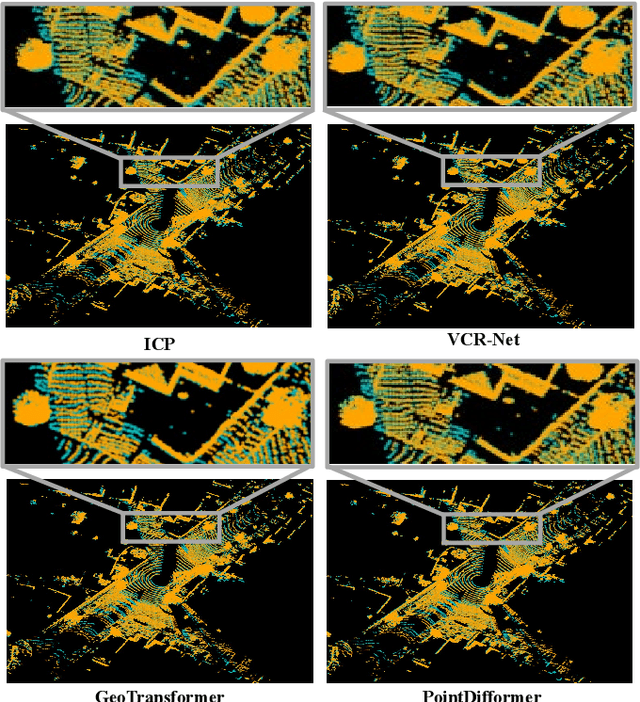
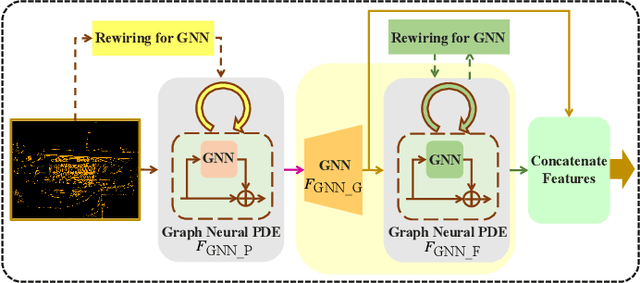
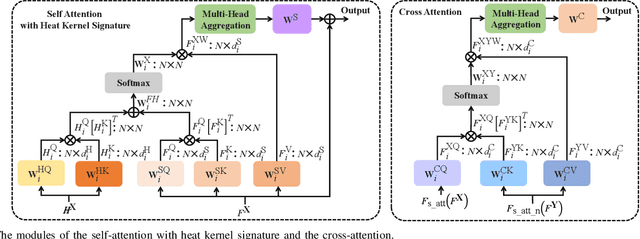
Point cloud registration is a fundamental technique in 3-D computer vision with applications in graphics, autonomous driving, and robotics. However, registration tasks under challenging conditions, under which noise or perturbations are prevalent, can be difficult. We propose a robust point cloud registration approach that leverages graph neural partial differential equations (PDEs) and heat kernel signatures. Our method first uses graph neural PDE modules to extract high dimensional features from point clouds by aggregating information from the 3-D point neighborhood, thereby enhancing the robustness of the feature representations. Then, we incorporate heat kernel signatures into an attention mechanism to efficiently obtain corresponding keypoints. Finally, a singular value decomposition (SVD) module with learnable weights is used to predict the transformation between two point clouds. Empirical experiments on a 3-D point cloud dataset demonstrate that our approach not only achieves state-of-the-art performance for point cloud registration but also exhibits better robustness to additive noise or 3-D shape perturbations.

Coupling Graph Neural Networks with Fractional Order Continuous Dynamics: A Robustness Study

In this work, we rigorously investigate the robustness of graph neural fractional-order differential equation (FDE) models. This framework extends beyond traditional graph neural (integer-order) ordinary differential equation (ODE) models by implementing the time-fractional Caputo derivative. Utilizing fractional calculus allows our model to consider long-term memory during the feature updating process, diverging from the memoryless Markovian updates seen in traditional graph neural ODE models. The superiority of graph neural FDE models over graph neural ODE models has been established in environments free from attacks or perturbations. While traditional graph neural ODE models have been verified to possess a degree of stability and resilience in the presence of adversarial attacks in existing literature, the robustness of graph neural FDE models, especially under adversarial conditions, remains largely unexplored. This paper undertakes a detailed assessment of the robustness of graph neural FDE models. We establish a theoretical foundation outlining the robustness characteristics of graph neural FDE models, highlighting that they maintain more stringent output perturbation bounds in the face of input and graph topology disturbances, compared to their integer-order counterparts. Our empirical evaluations further confirm the enhanced robustness of graph neural FDE models, highlighting their potential in adversarially robust applications.

PosDiffNet: Positional Neural Diffusion for Point Cloud Registration in a Large Field of View with Perturbations

Point cloud registration is a crucial technique in 3D computer vision with a wide range of applications. However, this task can be challenging, particularly in large fields of view with dynamic objects, environmental noise, or other perturbations. To address this challenge, we propose a model called PosDiffNet. Our approach performs hierarchical registration based on window-level, patch-level, and point-level correspondence. We leverage a graph neural partial differential equation (PDE) based on Beltrami flow to obtain high-dimensional features and position embeddings for point clouds. We incorporate position embeddings into a Transformer module based on a neural ordinary differential equation (ODE) to efficiently represent patches within points. We employ the multi-level correspondence derived from the high feature similarity scores to facilitate alignment between point clouds. Subsequently, we use registration methods such as SVD-based algorithms to predict the transformation using corresponding point pairs. We evaluate PosDiffNet on several 3D point cloud datasets, verifying that it achieves state-of-the-art (SOTA) performance for point cloud registration in large fields of view with perturbations. The implementation code of experiments is available at https://github.com/AI-IT-AVs/PosDiffNet.

DistilVPR: Cross-Modal Knowledge Distillation for Visual Place Recognition

The utilization of multi-modal sensor data in visual place recognition (VPR) has demonstrated enhanced performance compared to single-modal counterparts. Nonetheless, integrating additional sensors comes with elevated costs and may not be feasible for systems that demand lightweight operation, thereby impacting the practical deployment of VPR. To address this issue, we resort to knowledge distillation, which empowers single-modal students to learn from cross-modal teachers without introducing additional sensors during inference. Despite the notable advancements achieved by current distillation approaches, the exploration of feature relationships remains an under-explored area. In order to tackle the challenge of cross-modal distillation in VPR, we present DistilVPR, a novel distillation pipeline for VPR. We propose leveraging feature relationships from multiple agents, including self-agents and cross-agents for teacher and student neural networks. Furthermore, we integrate various manifolds, characterized by different space curvatures for exploring feature relationships. This approach enhances the diversity of feature relationships, including Euclidean, spherical, and hyperbolic relationship modules, thereby enhancing the overall representational capacity. The experiments demonstrate that our proposed pipeline achieves state-of-the-art performance compared to other distillation baselines. We also conduct necessary ablation studies to show design effectiveness. The code is released at: https://github.com/sijieaaa/DistilVPR

Image Patch-Matching with Graph-Based Learning in Street Scenes

Matching landmark patches from a real-time image captured by an on-vehicle camera with landmark patches in an image database plays an important role in various computer perception tasks for autonomous driving. Current methods focus on local matching for regions of interest and do not take into account spatial neighborhood relationships among the image patches, which typically correspond to objects in the environment. In this paper, we construct a spatial graph with the graph vertices corresponding to patches and edges capturing the spatial neighborhood information. We propose a joint feature and metric learning model with graph-based learning. We provide a theoretical basis for the graph-based loss by showing that the information distance between the distributions conditioned on matched and unmatched pairs is maximized under our framework. We evaluate our model using several street-scene datasets and demonstrate that our approach achieves state-of-the-art matching results.