Efficient Training of Neural Fractional-Order Differential Equation via Adjoint Backpropagation

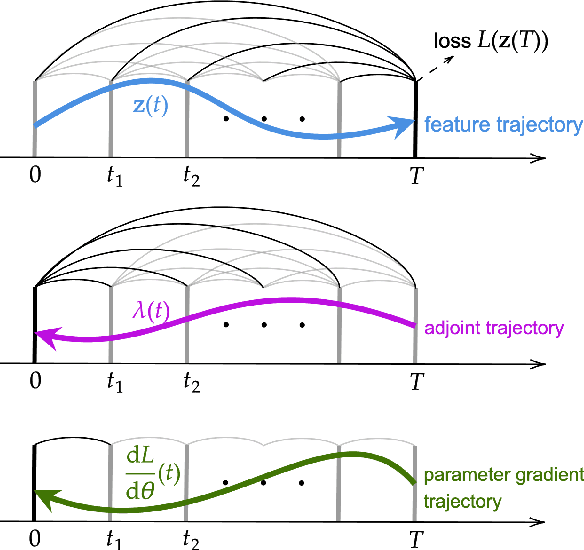
Fractional-order differential equations (FDEs) enhance traditional differential equations by extending the order of differential operators from integers to real numbers, offering greater flexibility in modeling complex dynamical systems with nonlocal characteristics. Recent progress at the intersection of FDEs and deep learning has catalyzed a new wave of innovative models, demonstrating the potential to address challenges such as graph representation learning. However, training neural FDEs has primarily relied on direct differentiation through forward-pass operations in FDE numerical solvers, leading to increased memory usage and computational complexity, particularly in large-scale applications. To address these challenges, we propose a scalable adjoint backpropagation method for training neural FDEs by solving an augmented FDE backward in time, which substantially reduces memory requirements. This approach provides a practical neural FDE toolbox and holds considerable promise for diverse applications. We demonstrate the effectiveness of our method in several tasks, achieving performance comparable to baseline models while significantly reducing computational overhead.