UAVScenes: A Multi-Modal Dataset for UAVs

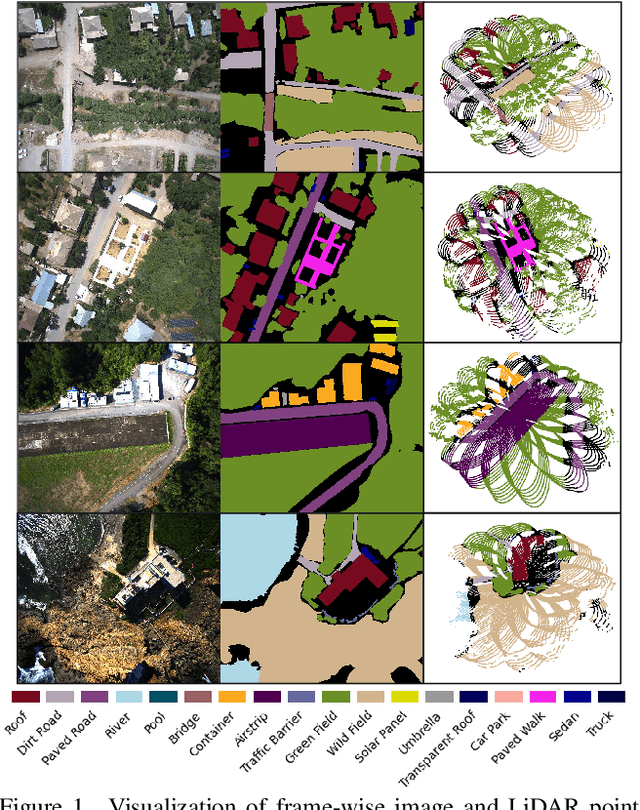
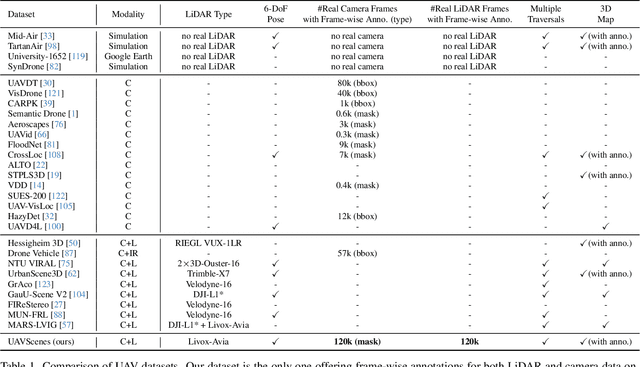
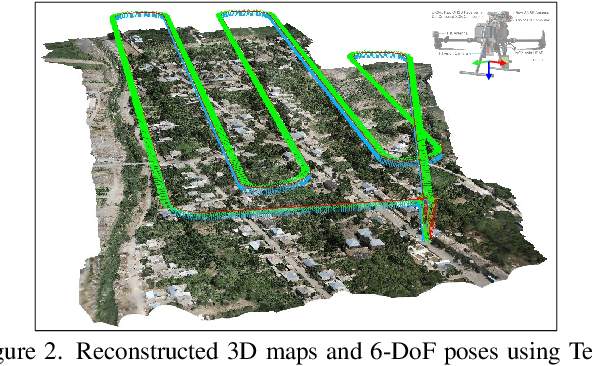
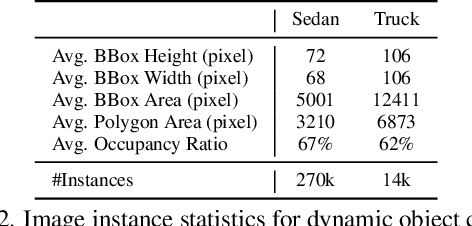
Multi-modal perception is essential for unmanned aerial vehicle (UAV) operations, as it enables a comprehensive understanding of the UAVs' surrounding environment. However, most existing multi-modal UAV datasets are primarily biased toward localization and 3D reconstruction tasks, or only support map-level semantic segmentation due to the lack of frame-wise annotations for both camera images and LiDAR point clouds. This limitation prevents them from being used for high-level scene understanding tasks. To address this gap and advance multi-modal UAV perception, we introduce UAVScenes, a large-scale dataset designed to benchmark various tasks across both 2D and 3D modalities. Our benchmark dataset is built upon the well-calibrated multi-modal UAV dataset MARS-LVIG, originally developed only for simultaneous localization and mapping (SLAM). We enhance this dataset by providing manually labeled semantic annotations for both frame-wise images and LiDAR point clouds, along with accurate 6-degree-of-freedom (6-DoF) poses. These additions enable a wide range of UAV perception tasks, including segmentation, depth estimation, 6-DoF localization, place recognition, and novel view synthesis (NVS). Our dataset is available at https://github.com/sijieaaa/UAVScenes

Simple Graph Contrastive Learning via Fractional-order Neural Diffusion Networks

Graph Contrastive Learning (GCL) has recently made progress as an unsupervised graph representation learning paradigm. GCL approaches can be categorized into augmentation-based and augmentation-free methods. The former relies on complex data augmentations, while the latter depends on encoders that can generate distinct views of the same input. Both approaches may require negative samples for training. In this paper, we introduce a novel augmentation-free GCL framework based on graph neural diffusion models. Specifically, we utilize learnable encoders governed by Fractional Differential Equations (FDE). Each FDE is characterized by an order parameter of the differential operator. We demonstrate that varying these parameters allows us to produce learnable encoders that generate diverse views, capturing either local or global information, for contrastive learning. Our model does not require negative samples for training and is applicable to both homophilic and heterophilic datasets. We demonstrate its effectiveness across various datasets, achieving state-of-the-art performance.

Efficient Training of Neural Fractional-Order Differential Equation via Adjoint Backpropagation

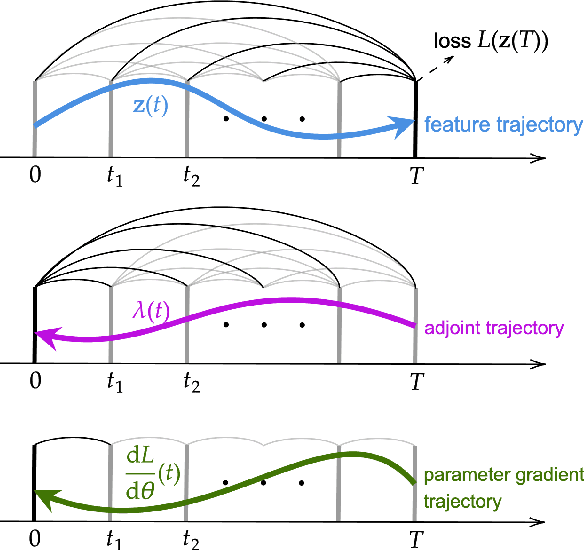
Fractional-order differential equations (FDEs) enhance traditional differential equations by extending the order of differential operators from integers to real numbers, offering greater flexibility in modeling complex dynamical systems with nonlocal characteristics. Recent progress at the intersection of FDEs and deep learning has catalyzed a new wave of innovative models, demonstrating the potential to address challenges such as graph representation learning. However, training neural FDEs has primarily relied on direct differentiation through forward-pass operations in FDE numerical solvers, leading to increased memory usage and computational complexity, particularly in large-scale applications. To address these challenges, we propose a scalable adjoint backpropagation method for training neural FDEs by solving an augmented FDE backward in time, which substantially reduces memory requirements. This approach provides a practical neural FDE toolbox and holds considerable promise for diverse applications. We demonstrate the effectiveness of our method in several tasks, achieving performance comparable to baseline models while significantly reducing computational overhead.

Neural Variable-Order Fractional Differential Equation Networks

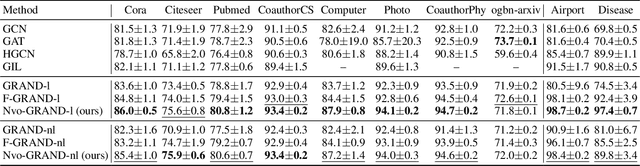
Neural differential equation models have garnered significant attention in recent years for their effectiveness in machine learning applications.Among these, fractional differential equations (FDEs) have emerged as a promising tool due to their ability to capture memory-dependent dynamics, which are often challenging to model with traditional integer-order approaches.While existing models have primarily focused on constant-order fractional derivatives, variable-order fractional operators offer a more flexible and expressive framework for modeling complex memory patterns. In this work, we introduce the Neural Variable-Order Fractional Differential Equation network (NvoFDE), a novel neural network framework that integrates variable-order fractional derivatives with learnable neural networks.Our framework allows for the modeling of adaptive derivative orders dependent on hidden features, capturing more complex feature-updating dynamics and providing enhanced flexibility. We conduct extensive experiments across multiple graph datasets to validate the effectiveness of our approach.Our results demonstrate that NvoFDE outperforms traditional constant-order fractional and integer models across a range of tasks, showcasing its superior adaptability and performance.

Distributed-Order Fractional Graph Operating Network

We introduce the Distributed-order fRActional Graph Operating Network (DRAGON), a novel continuous Graph Neural Network (GNN) framework that incorporates distributed-order fractional calculus. Unlike traditional continuous GNNs that utilize integer-order or single fractional-order differential equations, DRAGON uses a learnable probability distribution over a range of real numbers for the derivative orders. By allowing a flexible and learnable superposition of multiple derivative orders, our framework captures complex graph feature updating dynamics beyond the reach of conventional models. We provide a comprehensive interpretation of our framework's capability to capture intricate dynamics through the lens of a non-Markovian graph random walk with node feature updating driven by an anomalous diffusion process over the graph. Furthermore, to highlight the versatility of the DRAGON framework, we conduct empirical evaluations across a range of graph learning tasks. The results consistently demonstrate superior performance when compared to traditional continuous GNN models. The implementation code is available at \url{https://github.com/zknus/NeurIPS-2024-DRAGON}.

PRFusion: Toward Effective and Robust Multi-Modal Place Recognition with Image and Point Cloud Fusion

Place recognition plays a crucial role in the fields of robotics and computer vision, finding applications in areas such as autonomous driving, mapping, and localization. Place recognition identifies a place using query sensor data and a known database. One of the main challenges is to develop a model that can deliver accurate results while being robust to environmental variations. We propose two multi-modal place recognition models, namely PRFusion and PRFusion++. PRFusion utilizes global fusion with manifold metric attention, enabling effective interaction between features without requiring camera-LiDAR extrinsic calibrations. In contrast, PRFusion++ assumes the availability of extrinsic calibrations and leverages pixel-point correspondences to enhance feature learning on local windows. Additionally, both models incorporate neural diffusion layers, which enable reliable operation even in challenging environments. We verify the state-of-the-art performance of both models on three large-scale benchmarks. Notably, they outperform existing models by a substantial margin of +3.0 AR@1 on the demanding Boreas dataset. Furthermore, we conduct ablation studies to validate the effectiveness of our proposed methods. The codes are available at: https://github.com/sijieaaa/PRFusion

Generalized Graph Signal Reconstruction via the Uncertainty Principle

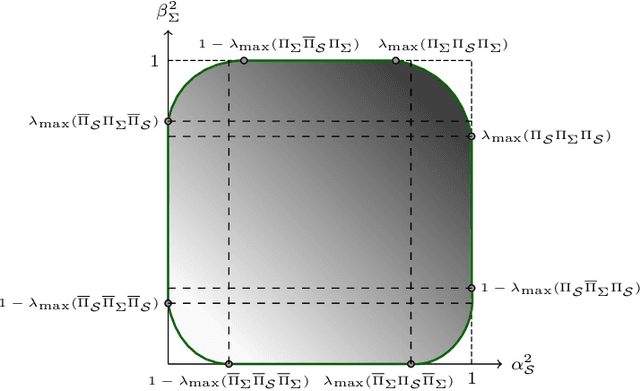
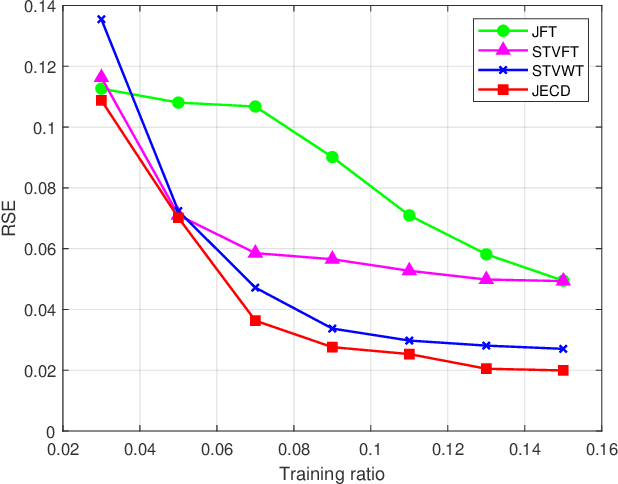
We introduce a novel uncertainty principle for generalized graph signals that extends classical time-frequency and graph uncertainty principles into a unified framework. By defining joint vertex-time and spectral-frequency spreads, we quantify signal localization across these domains, revealing a trade-off between them. This framework allows us to identify a class of signals with maximal energy concentration in both domains, forming the fundamental atoms for a new joint vertex-time dictionary. This dictionary enhances signal reconstruction under practical constraints, such as incomplete or intermittent data, commonly encountered in sensor and social networks. Numerical experiments on real-world datasets demonstrate the effectiveness of the proposed approach, showing improved reconstruction accuracy and noise robustness compared to existing methods.

A Graph Signal Processing Perspective of Network Multiple Hypothesis Testing with False Discovery Rate Control

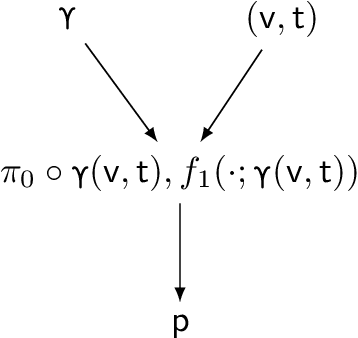
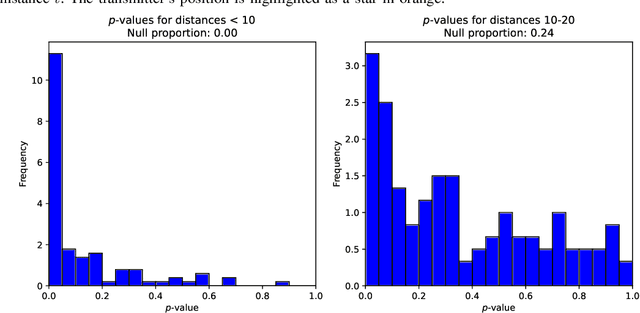
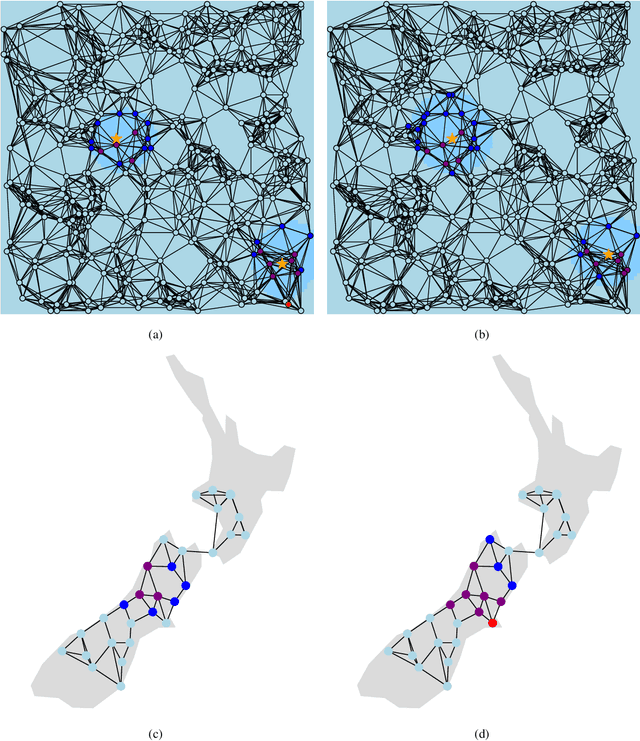
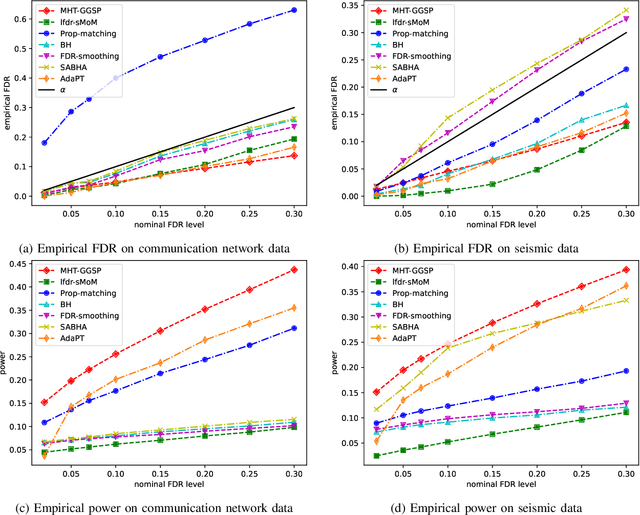
We consider a multiple hypothesis testing problem in a sensor network over the joint spatial-time domain. The sensor network is modeled as a graph, with each vertex representing a sensor and a signal over time associated with each vertex. We assume a hypothesis test and an associated p-value for every sample point in the joint spatial-time domain. Our goal is to determine which points have true alternative hypotheses. By parameterizing the unknown alternative distribution of $p$-values and the prior probabilities of hypotheses being null with a bandlimited generalized graph signal, we can obtain consistent estimates for them. Consequently, we also obtain an estimate of the local false discovery rates (lfdr). We prove that by using a step-up procedure on the estimated lfdr, we can achieve asymptotic false discovery rate control at a pre-determined level. Numerical experiments validate the effectiveness of our approach compared to existing methods.

FedSheafHN: Personalized Federated Learning on Graph-structured Data

Personalized subgraph Federated Learning (FL) is a task that customizes Graph Neural Networks (GNNs) to individual client needs, accommodating diverse data distributions. However, applying hypernetworks in FL, while aiming to facilitate model personalization, often encounters challenges due to inadequate representation of client-specific characteristics. To overcome these limitations, we propose a model called FedSheafHN, using enhanced collaboration graph embedding and efficient personalized model parameter generation. Specifically, our model embeds each client's local subgraph into a server-constructed collaboration graph. We utilize sheaf diffusion in the collaboration graph to learn client representations. Our model improves the integration and interpretation of complex client characteristics. Furthermore, our model ensures the generation of personalized models through advanced hypernetworks optimized for parallel operations across clients. Empirical evaluations demonstrate that FedSheafHN outperforms existing methods in most scenarios, in terms of client model performance on various graph-structured datasets. It also has fast model convergence and effective new clients generalization.

Hybrid Event-Frame Neural Spike Detector for Neuromorphic Implantable BMI

This work introduces two novel neural spike detection schemes intended for use in next-generation neuromorphic brain-machine interfaces (iBMIs). The first, an Event-based Spike Detector (Ev-SPD) which examines the temporal neighborhood of a neural event for spike detection, is designed for in-vivo processing and offers high sensitivity and decent accuracy (94-97%). The second, Neural Network-based Spike Detector (NN-SPD) which operates on hybrid temporal event frames, provides an off-implant solution using shallow neural networks with impressive detection accuracy (96-99%) and minimal false detections. These methods are evaluated using a synthetic dataset with varying noise levels and validated through comparison with ground truth data. The results highlight their potential in next-gen neuromorphic iBMI systems and emphasize the need to explore this direction further to understand their resource-efficient and high-performance capabilities for practical iBMI settings.