Distributed-Order Fractional Graph Operating Network

We introduce the Distributed-order fRActional Graph Operating Network (DRAGON), a novel continuous Graph Neural Network (GNN) framework that incorporates distributed-order fractional calculus. Unlike traditional continuous GNNs that utilize integer-order or single fractional-order differential equations, DRAGON uses a learnable probability distribution over a range of real numbers for the derivative orders. By allowing a flexible and learnable superposition of multiple derivative orders, our framework captures complex graph feature updating dynamics beyond the reach of conventional models. We provide a comprehensive interpretation of our framework's capability to capture intricate dynamics through the lens of a non-Markovian graph random walk with node feature updating driven by an anomalous diffusion process over the graph. Furthermore, to highlight the versatility of the DRAGON framework, we conduct empirical evaluations across a range of graph learning tasks. The results consistently demonstrate superior performance when compared to traditional continuous GNN models. The implementation code is available at \url{https://github.com/zknus/NeurIPS-2024-DRAGON}.

Unleashing the Potential of Fractional Calculus in Graph Neural Networks with FROND

We introduce the FRactional-Order graph Neural Dynamical network (FROND), a new continuous graph neural network (GNN) framework. Unlike traditional continuous GNNs that rely on integer-order differential equations, FROND employs the Caputo fractional derivative to leverage the non-local properties of fractional calculus. This approach enables the capture of long-term dependencies in feature updates, moving beyond the Markovian update mechanisms in conventional integer-order models and offering enhanced capabilities in graph representation learning. We offer an interpretation of the node feature updating process in FROND from a non-Markovian random walk perspective when the feature updating is particularly governed by a diffusion process. We demonstrate analytically that oversmoothing can be mitigated in this setting. Experimentally, we validate the FROND framework by comparing the fractional adaptations of various established integer-order continuous GNNs, demonstrating their consistently improved performance and underscoring the framework's potential as an effective extension to enhance traditional continuous GNNs. The code is available at \url{https://github.com/zknus/ICLR2024-FROND}.

Stable Neural ODE with Lyapunov-Stable Equilibrium Points for Defending Against Adversarial Attacks

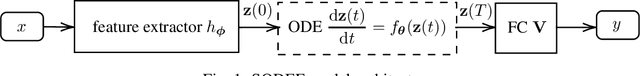
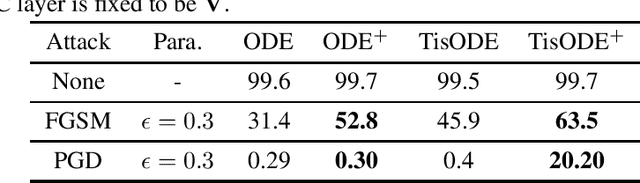
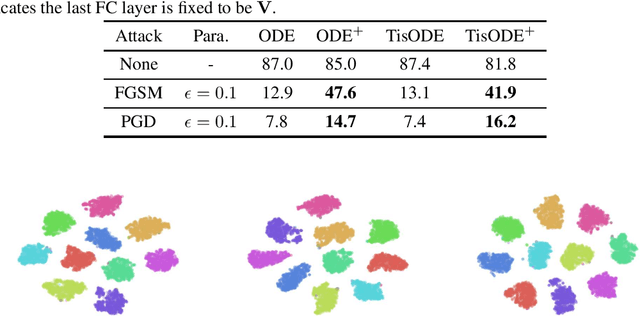
Deep neural networks (DNNs) are well-known to be vulnerable to adversarial attacks, where malicious human-imperceptible perturbations are included in the input to the deep network to fool it into making a wrong classification. Recent studies have demonstrated that neural Ordinary Differential Equations (ODEs) are intrinsically more robust against adversarial attacks compared to vanilla DNNs. In this work, we propose a stable neural ODE with Lyapunov-stable equilibrium points for defending against adversarial attacks (SODEF). By ensuring that the equilibrium points of the ODE solution used as part of SODEF is Lyapunov-stable, the ODE solution for an input with a small perturbation converges to the same solution as the unperturbed input. We provide theoretical results that give insights into the stability of SODEF as well as the choice of regularizers to ensure its stability. Our analysis suggests that our proposed regularizers force the extracted feature points to be within a neighborhood of the Lyapunov-stable equilibrium points of the ODE. SODEF is compatible with many defense methods and can be applied to any neural network's final regressor layer to enhance its stability against adversarial attacks.

A Hybrid Bandit Framework for Diversified Recommendation

The interactive recommender systems involve users in the recommendation procedure by receiving timely user feedback to update the recommendation policy. Therefore, they are widely used in real application scenarios. Previous interactive recommendation methods primarily focus on learning users' personalized preferences on the relevance properties of an item set. However, the investigation of users' personalized preferences on the diversity properties of an item set is usually ignored. To overcome this problem, we propose the Linear Modular Dispersion Bandit (LMDB) framework, which is an online learning setting for optimizing a combination of modular functions and dispersion functions. Specifically, LMDB employs modular functions to model the relevance properties of each item, and dispersion functions to describe the diversity properties of an item set. Moreover, we also develop a learning algorithm, called Linear Modular Dispersion Hybrid (LMDH) to solve the LMDB problem and derive a gap-free bound on its n-step regret. Extensive experiments on real datasets are performed to demonstrate the effectiveness of the proposed LMDB framework in balancing the recommendation accuracy and diversity.