Stable Neural ODE with Lyapunov-Stable Equilibrium Points for Defending Against Adversarial Attacks
Paper and Code
Oct 25, 2021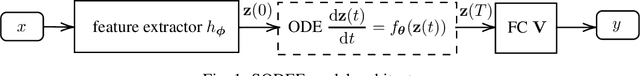
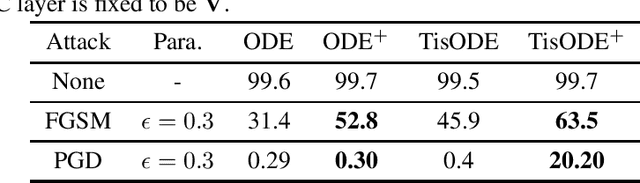
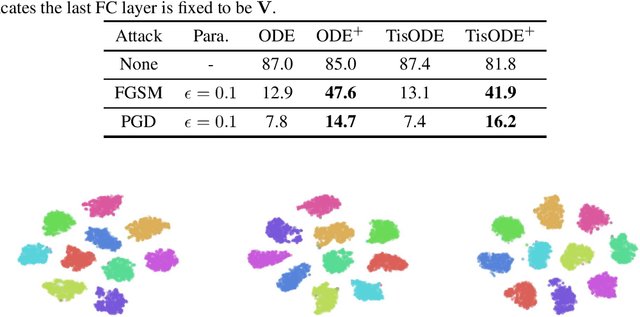

Deep neural networks (DNNs) are well-known to be vulnerable to adversarial attacks, where malicious human-imperceptible perturbations are included in the input to the deep network to fool it into making a wrong classification. Recent studies have demonstrated that neural Ordinary Differential Equations (ODEs) are intrinsically more robust against adversarial attacks compared to vanilla DNNs. In this work, we propose a stable neural ODE with Lyapunov-stable equilibrium points for defending against adversarial attacks (SODEF). By ensuring that the equilibrium points of the ODE solution used as part of SODEF is Lyapunov-stable, the ODE solution for an input with a small perturbation converges to the same solution as the unperturbed input. We provide theoretical results that give insights into the stability of SODEF as well as the choice of regularizers to ensure its stability. Our analysis suggests that our proposed regularizers force the extracted feature points to be within a neighborhood of the Lyapunov-stable equilibrium points of the ODE. SODEF is compatible with many defense methods and can be applied to any neural network's final regressor layer to enhance its stability against adversarial attacks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge