Yanan Zhao
Simple Graph Contrastive Learning via Fractional-order Neural Diffusion Networks
Apr 24, 2025Abstract:Graph Contrastive Learning (GCL) has recently made progress as an unsupervised graph representation learning paradigm. GCL approaches can be categorized into augmentation-based and augmentation-free methods. The former relies on complex data augmentations, while the latter depends on encoders that can generate distinct views of the same input. Both approaches may require negative samples for training. In this paper, we introduce a novel augmentation-free GCL framework based on graph neural diffusion models. Specifically, we utilize learnable encoders governed by Fractional Differential Equations (FDE). Each FDE is characterized by an order parameter of the differential operator. We demonstrate that varying these parameters allows us to produce learnable encoders that generate diverse views, capturing either local or global information, for contrastive learning. Our model does not require negative samples for training and is applicable to both homophilic and heterophilic datasets. We demonstrate its effectiveness across various datasets, achieving state-of-the-art performance.
Efficient Training of Neural Fractional-Order Differential Equation via Adjoint Backpropagation
Mar 20, 2025
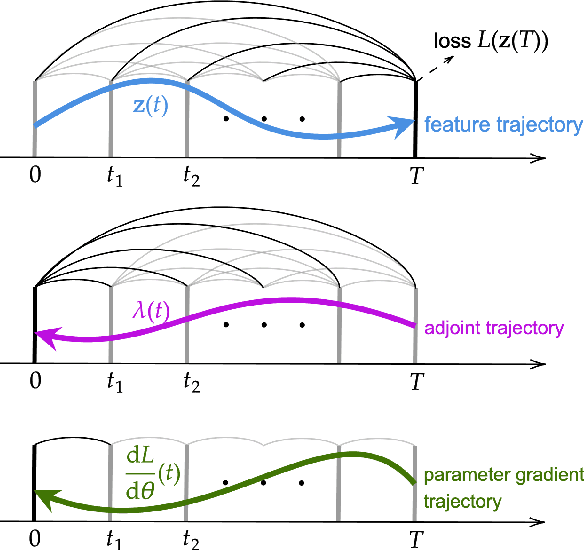


Abstract:Fractional-order differential equations (FDEs) enhance traditional differential equations by extending the order of differential operators from integers to real numbers, offering greater flexibility in modeling complex dynamical systems with nonlocal characteristics. Recent progress at the intersection of FDEs and deep learning has catalyzed a new wave of innovative models, demonstrating the potential to address challenges such as graph representation learning. However, training neural FDEs has primarily relied on direct differentiation through forward-pass operations in FDE numerical solvers, leading to increased memory usage and computational complexity, particularly in large-scale applications. To address these challenges, we propose a scalable adjoint backpropagation method for training neural FDEs by solving an augmented FDE backward in time, which substantially reduces memory requirements. This approach provides a practical neural FDE toolbox and holds considerable promise for diverse applications. We demonstrate the effectiveness of our method in several tasks, achieving performance comparable to baseline models while significantly reducing computational overhead.
Distributed-Order Fractional Graph Operating Network
Nov 08, 2024



Abstract:We introduce the Distributed-order fRActional Graph Operating Network (DRAGON), a novel continuous Graph Neural Network (GNN) framework that incorporates distributed-order fractional calculus. Unlike traditional continuous GNNs that utilize integer-order or single fractional-order differential equations, DRAGON uses a learnable probability distribution over a range of real numbers for the derivative orders. By allowing a flexible and learnable superposition of multiple derivative orders, our framework captures complex graph feature updating dynamics beyond the reach of conventional models. We provide a comprehensive interpretation of our framework's capability to capture intricate dynamics through the lens of a non-Markovian graph random walk with node feature updating driven by an anomalous diffusion process over the graph. Furthermore, to highlight the versatility of the DRAGON framework, we conduct empirical evaluations across a range of graph learning tasks. The results consistently demonstrate superior performance when compared to traditional continuous GNN models. The implementation code is available at \url{https://github.com/zknus/NeurIPS-2024-DRAGON}.
Generalized Graph Signal Reconstruction via the Uncertainty Principle
Sep 06, 2024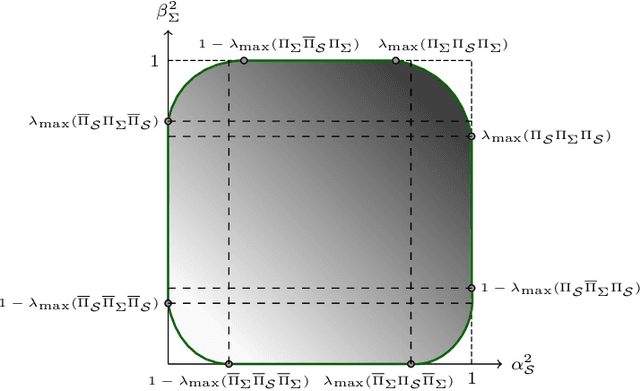
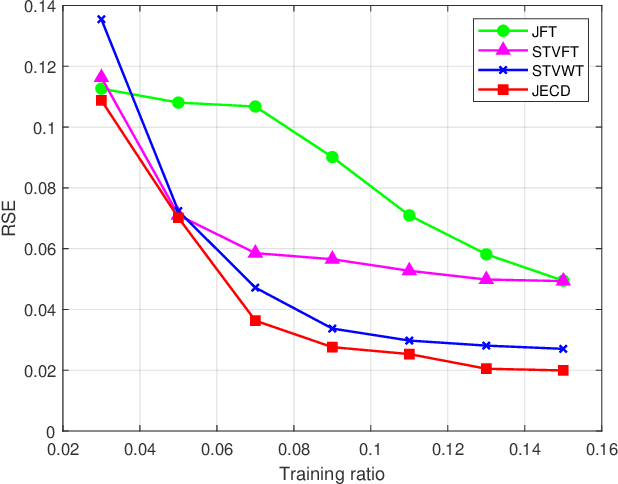
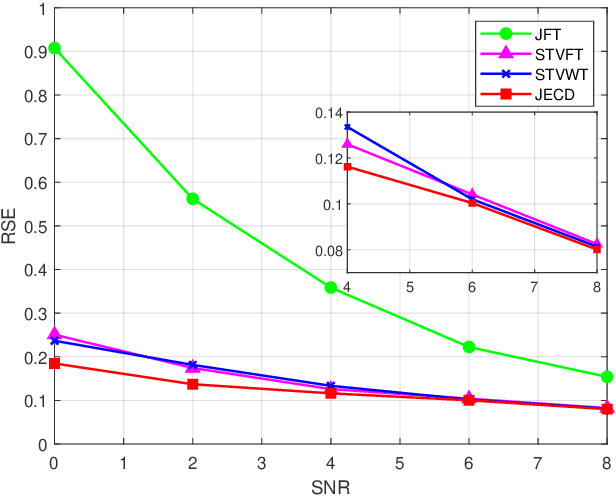
Abstract:We introduce a novel uncertainty principle for generalized graph signals that extends classical time-frequency and graph uncertainty principles into a unified framework. By defining joint vertex-time and spectral-frequency spreads, we quantify signal localization across these domains, revealing a trade-off between them. This framework allows us to identify a class of signals with maximal energy concentration in both domains, forming the fundamental atoms for a new joint vertex-time dictionary. This dictionary enhances signal reconstruction under practical constraints, such as incomplete or intermittent data, commonly encountered in sensor and social networks. Numerical experiments on real-world datasets demonstrate the effectiveness of the proposed approach, showing improved reconstruction accuracy and noise robustness compared to existing methods.
FedSheafHN: Personalized Federated Learning on Graph-structured Data
May 25, 2024Abstract:Personalized subgraph Federated Learning (FL) is a task that customizes Graph Neural Networks (GNNs) to individual client needs, accommodating diverse data distributions. However, applying hypernetworks in FL, while aiming to facilitate model personalization, often encounters challenges due to inadequate representation of client-specific characteristics. To overcome these limitations, we propose a model called FedSheafHN, using enhanced collaboration graph embedding and efficient personalized model parameter generation. Specifically, our model embeds each client's local subgraph into a server-constructed collaboration graph. We utilize sheaf diffusion in the collaboration graph to learn client representations. Our model improves the integration and interpretation of complex client characteristics. Furthermore, our model ensures the generation of personalized models through advanced hypernetworks optimized for parallel operations across clients. Empirical evaluations demonstrate that FedSheafHN outperforms existing methods in most scenarios, in terms of client model performance on various graph-structured datasets. It also has fast model convergence and effective new clients generalization.
Deep, convergent, unrolled half-quadratic splitting for image deconvolution
Feb 25, 2024



Abstract:In recent years, algorithm unrolling has emerged as a powerful technique for designing interpretable neural networks based on iterative algorithms. Imaging inverse problems have particularly benefited from unrolling-based deep network design since many traditional model-based approaches rely on iterative optimization. Despite exciting progress, typical unrolling approaches heuristically design layer-specific convolution weights to improve performance. Crucially, convergence properties of the underlying iterative algorithm are lost once layer-specific parameters are learned from training data. We propose an unrolling technique that breaks the trade-off between retaining algorithm properties while simultaneously enhancing performance. We focus on image deblurring and unrolling the widely-applied Half-Quadratic Splitting (HQS) algorithm. We develop a new parametrization scheme which enforces layer-specific parameters to asymptotically approach certain fixed points. Through extensive experimental studies, we verify that our approach achieves competitive performance with state-of-the-art unrolled layer-specific learning and significantly improves over the traditional HQS algorithm. We further establish convergence of the proposed unrolled network as the number of layers approaches infinity, and characterize its convergence rate. Our experimental verification involves simulations that validate the analytical results as well as comparison with state-of-the-art non-blind deblurring techniques on benchmark datasets. The merits of the proposed convergent unrolled network are established over competing alternatives, especially in the regime of limited training.
Coupling Graph Neural Networks with Fractional Order Continuous Dynamics: A Robustness Study
Jan 09, 2024



Abstract:In this work, we rigorously investigate the robustness of graph neural fractional-order differential equation (FDE) models. This framework extends beyond traditional graph neural (integer-order) ordinary differential equation (ODE) models by implementing the time-fractional Caputo derivative. Utilizing fractional calculus allows our model to consider long-term memory during the feature updating process, diverging from the memoryless Markovian updates seen in traditional graph neural ODE models. The superiority of graph neural FDE models over graph neural ODE models has been established in environments free from attacks or perturbations. While traditional graph neural ODE models have been verified to possess a degree of stability and resilience in the presence of adversarial attacks in existing literature, the robustness of graph neural FDE models, especially under adversarial conditions, remains largely unexplored. This paper undertakes a detailed assessment of the robustness of graph neural FDE models. We establish a theoretical foundation outlining the robustness characteristics of graph neural FDE models, highlighting that they maintain more stringent output perturbation bounds in the face of input and graph topology disturbances, compared to their integer-order counterparts. Our empirical evaluations further confirm the enhanced robustness of graph neural FDE models, highlighting their potential in adversarially robust applications.
SSN: Stockwell Scattering Network for SAR Image Change Detection
Apr 22, 2023



Abstract:Recently, synthetic aperture radar (SAR) image change detection has become an interesting yet challenging direction due to the presence of speckle noise. Although both traditional and modern learning-driven methods attempted to overcome this challenge, deep convolutional neural networks (DCNNs)-based methods are still hindered by the lack of interpretability and the requirement of large computation power. To overcome this drawback, wavelet scattering network (WSN) and Fourier scattering network (FSN) are proposed. Combining respective merits of WSN and FSN, we propose Stockwell scattering network (SSN) based on Stockwell transform which is widely applied against noisy signals and shows advantageous characteristics in speckle reduction. The proposed SSN provides noise-resilient feature representation and obtains state-of-art performance in SAR image change detection as well as high computational efficiency. Experimental results on three real SAR image datasets demonstrate the effectiveness of the proposed method.
* 5 pages, 6 figures
A Comparative Study of Deep Reinforcement Learning-based Transferable Energy Management Strategies for Hybrid Electric Vehicles
Feb 22, 2022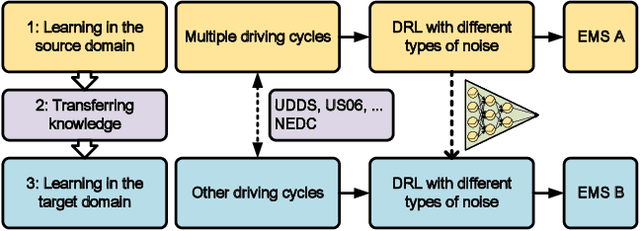
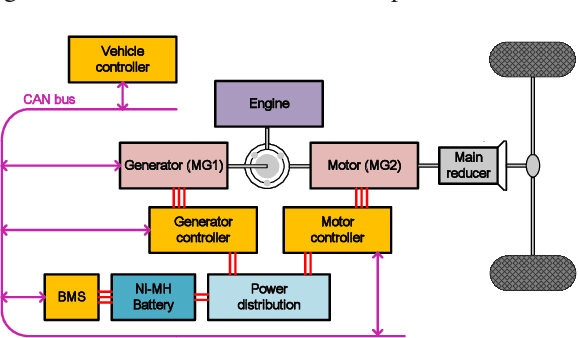
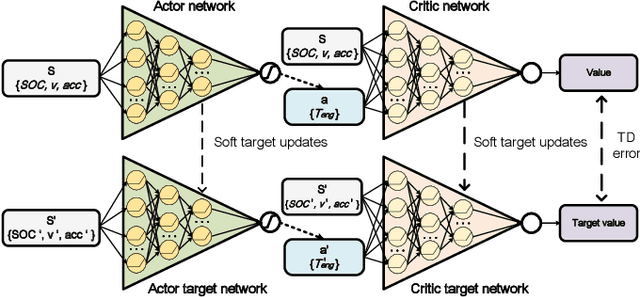
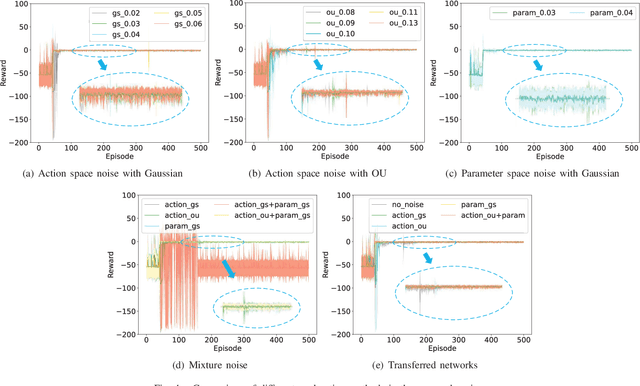
Abstract:The deep reinforcement learning-based energy management strategies (EMS) has become a promising solution for hybrid electric vehicles (HEVs). When driving cycles are changed, the network will be retrained, which is a time-consuming and laborious task. A more efficient way of choosing EMS is to combine deep reinforcement learning (DRL) with transfer learning, which can transfer knowledge of one domain to the other new domain, making the network of the new domain reach convergence values quickly. Different exploration methods of RL, including adding action space noise and parameter space noise, are compared against each other in the transfer learning process in this work. Results indicate that the network added parameter space noise is more stable and faster convergent than the others. In conclusion, the best exploration method for transferable EMS is to add noise in the parameter space, while the combination of action space noise and parameter space noise generally performs poorly. Our code is available at https://github.com/BIT-XJY/RL-based-Transferable-EMS.git.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge