Neural Variable-Order Fractional Differential Equation Networks

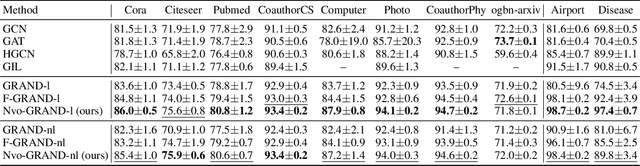
Neural differential equation models have garnered significant attention in recent years for their effectiveness in machine learning applications.Among these, fractional differential equations (FDEs) have emerged as a promising tool due to their ability to capture memory-dependent dynamics, which are often challenging to model with traditional integer-order approaches.While existing models have primarily focused on constant-order fractional derivatives, variable-order fractional operators offer a more flexible and expressive framework for modeling complex memory patterns. In this work, we introduce the Neural Variable-Order Fractional Differential Equation network (NvoFDE), a novel neural network framework that integrates variable-order fractional derivatives with learnable neural networks.Our framework allows for the modeling of adaptive derivative orders dependent on hidden features, capturing more complex feature-updating dynamics and providing enhanced flexibility. We conduct extensive experiments across multiple graph datasets to validate the effectiveness of our approach.Our results demonstrate that NvoFDE outperforms traditional constant-order fractional and integer models across a range of tasks, showcasing its superior adaptability and performance.

Efficient Training of Neural Fractional-Order Differential Equation via Adjoint Backpropagation

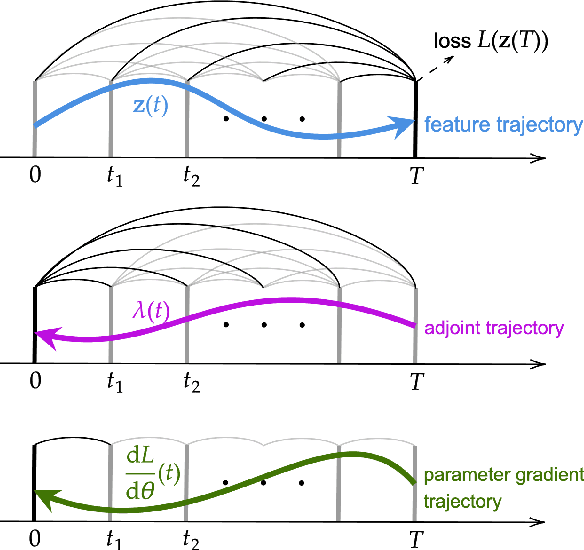
Fractional-order differential equations (FDEs) enhance traditional differential equations by extending the order of differential operators from integers to real numbers, offering greater flexibility in modeling complex dynamical systems with nonlocal characteristics. Recent progress at the intersection of FDEs and deep learning has catalyzed a new wave of innovative models, demonstrating the potential to address challenges such as graph representation learning. However, training neural FDEs has primarily relied on direct differentiation through forward-pass operations in FDE numerical solvers, leading to increased memory usage and computational complexity, particularly in large-scale applications. To address these challenges, we propose a scalable adjoint backpropagation method for training neural FDEs by solving an augmented FDE backward in time, which substantially reduces memory requirements. This approach provides a practical neural FDE toolbox and holds considerable promise for diverse applications. We demonstrate the effectiveness of our method in several tasks, achieving performance comparable to baseline models while significantly reducing computational overhead.

Distributed-Order Fractional Graph Operating Network

We introduce the Distributed-order fRActional Graph Operating Network (DRAGON), a novel continuous Graph Neural Network (GNN) framework that incorporates distributed-order fractional calculus. Unlike traditional continuous GNNs that utilize integer-order or single fractional-order differential equations, DRAGON uses a learnable probability distribution over a range of real numbers for the derivative orders. By allowing a flexible and learnable superposition of multiple derivative orders, our framework captures complex graph feature updating dynamics beyond the reach of conventional models. We provide a comprehensive interpretation of our framework's capability to capture intricate dynamics through the lens of a non-Markovian graph random walk with node feature updating driven by an anomalous diffusion process over the graph. Furthermore, to highlight the versatility of the DRAGON framework, we conduct empirical evaluations across a range of graph learning tasks. The results consistently demonstrate superior performance when compared to traditional continuous GNN models. The implementation code is available at \url{https://github.com/zknus/NeurIPS-2024-DRAGON}.

Unleashing the Potential of Fractional Calculus in Graph Neural Networks with FROND

We introduce the FRactional-Order graph Neural Dynamical network (FROND), a new continuous graph neural network (GNN) framework. Unlike traditional continuous GNNs that rely on integer-order differential equations, FROND employs the Caputo fractional derivative to leverage the non-local properties of fractional calculus. This approach enables the capture of long-term dependencies in feature updates, moving beyond the Markovian update mechanisms in conventional integer-order models and offering enhanced capabilities in graph representation learning. We offer an interpretation of the node feature updating process in FROND from a non-Markovian random walk perspective when the feature updating is particularly governed by a diffusion process. We demonstrate analytically that oversmoothing can be mitigated in this setting. Experimentally, we validate the FROND framework by comparing the fractional adaptations of various established integer-order continuous GNNs, demonstrating their consistently improved performance and underscoring the framework's potential as an effective extension to enhance traditional continuous GNNs. The code is available at \url{https://github.com/zknus/ICLR2024-FROND}.

Toward Explainable and Fine-Grained 3D Grounding through Referring Textual Phrases

Recent progress on 3D scene understanding has explored visual grounding (3DVG) to localize a target object through a language description. However, existing methods only consider the dependency between the entire sentence and the target object, thus ignoring fine-grained relationships between contexts and non-target ones. In this paper, we extend 3DVG to a more reliable and explainable task, called 3D Phrase Aware Grounding (3DPAG). The 3DPAG task aims to localize the target object in the 3D scenes by explicitly identifying all phrase-related objects and then conducting reasoning according to contextual phrases. To tackle this problem, we label about 400K phrase-level annotations from 170K sentences in available 3DVG datasets, i.e., Nr3D, Sr3D and ScanRefer. By tapping on these developed datasets, we propose a novel framework, i.e., PhraseRefer, which conducts phrase-aware and object-level representation learning through phrase-object alignment optimization as well as phrase-specific pre-training. In our setting, we extend previous 3DVG methods to the phrase-aware scenario and provide metrics to measure the explainability of the 3DPAG task. Extensive results confirm that 3DPAG effectively boosts the 3DVG, and PhraseRefer achieves state-of-the-arts across three datasets, i.e., 63.0%, 54.4% and 55.5% overall accuracy on Sr3D, Nr3D and ScanRefer, respectively.