Simple Graph Contrastive Learning via Fractional-order Neural Diffusion Networks

Graph Contrastive Learning (GCL) has recently made progress as an unsupervised graph representation learning paradigm. GCL approaches can be categorized into augmentation-based and augmentation-free methods. The former relies on complex data augmentations, while the latter depends on encoders that can generate distinct views of the same input. Both approaches may require negative samples for training. In this paper, we introduce a novel augmentation-free GCL framework based on graph neural diffusion models. Specifically, we utilize learnable encoders governed by Fractional Differential Equations (FDE). Each FDE is characterized by an order parameter of the differential operator. We demonstrate that varying these parameters allows us to produce learnable encoders that generate diverse views, capturing either local or global information, for contrastive learning. Our model does not require negative samples for training and is applicable to both homophilic and heterophilic datasets. We demonstrate its effectiveness across various datasets, achieving state-of-the-art performance.

Falcon: Faster and Parallel Inference of Large Language Models through Enhanced Semi-Autoregressive Drafting and Custom-Designed Decoding Tree

Striking an optimal balance between minimal drafting latency and high speculation accuracy to enhance the inference speed of Large Language Models remains a significant challenge in speculative decoding. In this paper, we introduce Falcon, an innovative semi-autoregressive speculative decoding framework fashioned to augment both the drafter's parallelism and output quality. Falcon incorporates the Coupled Sequential Glancing Distillation technique, which fortifies inter-token dependencies within the same block, leading to increased speculation accuracy. We offer a comprehensive theoretical analysis to illuminate the underlying mechanisms. Additionally, we introduce a Custom-Designed Decoding Tree, which permits the drafter to generate multiple tokens in a single forward pass and accommodates multiple forward passes as needed, thereby boosting the number of drafted tokens and significantly improving the overall acceptance rate. Comprehensive evaluations on benchmark datasets such as MT-Bench, HumanEval, and GSM8K demonstrate Falcon's superior acceleration capabilities. The framework achieves a lossless speedup ratio ranging from 2.91x to 3.51x when tested on the Vicuna and LLaMA2-Chat model series. These results outstrip existing speculative decoding methods for LLMs, including Eagle, Medusa, Lookahead, SPS, and PLD, while maintaining a compact drafter architecture equivalent to merely two Transformer layers.

Distributed-Order Fractional Graph Operating Network

We introduce the Distributed-order fRActional Graph Operating Network (DRAGON), a novel continuous Graph Neural Network (GNN) framework that incorporates distributed-order fractional calculus. Unlike traditional continuous GNNs that utilize integer-order or single fractional-order differential equations, DRAGON uses a learnable probability distribution over a range of real numbers for the derivative orders. By allowing a flexible and learnable superposition of multiple derivative orders, our framework captures complex graph feature updating dynamics beyond the reach of conventional models. We provide a comprehensive interpretation of our framework's capability to capture intricate dynamics through the lens of a non-Markovian graph random walk with node feature updating driven by an anomalous diffusion process over the graph. Furthermore, to highlight the versatility of the DRAGON framework, we conduct empirical evaluations across a range of graph learning tasks. The results consistently demonstrate superior performance when compared to traditional continuous GNN models. The implementation code is available at \url{https://github.com/zknus/NeurIPS-2024-DRAGON}.

Edge centrality and the total variation of graph distributional signals

This short note is a supplement to [1], in which the total variation of graph distributional signals is introduced and studied. We introduce a different formulation of total variation and relate it to the notion of edge centrality. The relation provides a different perspective of total variation and may facilitate its computation.

Control the GNN: Utilizing Neural Controller with Lyapunov Stability for Test-Time Feature Reconstruction

The performance of graph neural networks (GNNs) is susceptible to discrepancies between training and testing sample distributions. Prior studies have attempted to enhance GNN performance by reconstructing node features during the testing phase without modifying the model parameters. However, these approaches lack theoretical analysis of the proximity between predictions and ground truth at test time. In this paper, we propose a novel node feature reconstruction method grounded in Lyapunov stability theory. Specifically, we model the GNN as a control system during the testing phase, considering node features as control variables. A neural controller that adheres to the Lyapunov stability criterion is then employed to reconstruct these node features, ensuring that the predictions progressively approach the ground truth at test time. We validate the effectiveness of our approach through extensive experiments across multiple datasets, demonstrating significant performance improvements.

The Transferability of Downsamped Sparse Graph Convolutional Networks

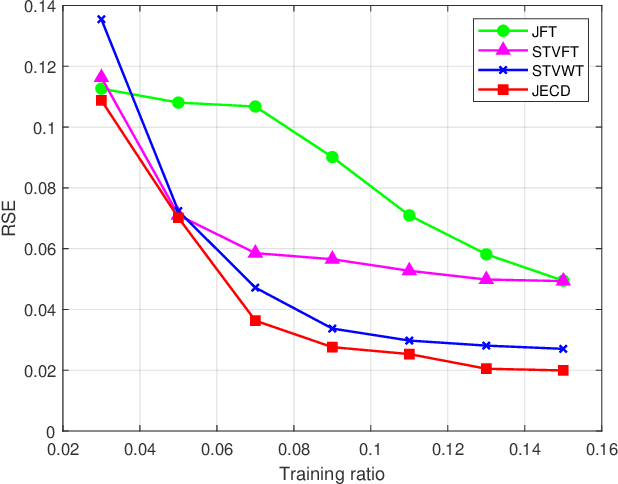
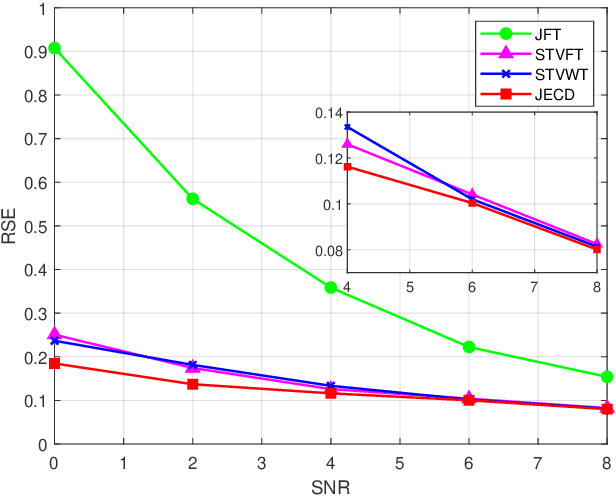
To accelerate the training of graph convolutional networks (GCNs) on real-world large-scale sparse graphs, downsampling methods are commonly employed as a preprocessing step. However, the effects of graph sparsity and topological structure on the transferability of downsampling methods have not been rigorously analyzed or theoretically guaranteed, particularly when the topological structure is affected by graph sparsity. In this paper, we introduce a novel downsampling method based on a sparse random graph model and derive an expected upper bound for the transfer error. Our findings show that smaller original graph sizes, higher expected average degrees, and increased sampling rates contribute to reducing this upper bound. Experimental results validate the theoretical predictions. By incorporating both sparsity and topological similarity into the model, this study establishes an upper bound on the transfer error for downsampling in the training of large-scale sparse graphs and provides insight into the influence of topological structure on transfer performance.

Generalized Graph Signal Reconstruction via the Uncertainty Principle

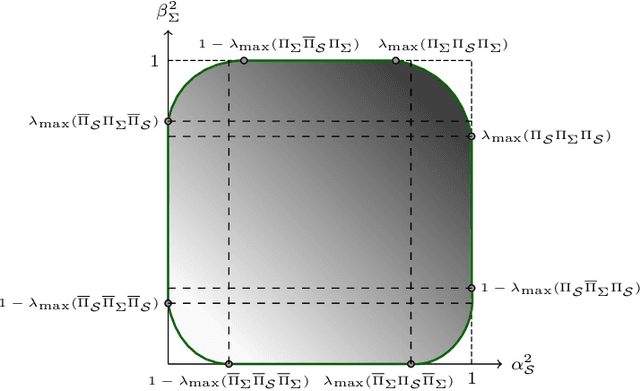
We introduce a novel uncertainty principle for generalized graph signals that extends classical time-frequency and graph uncertainty principles into a unified framework. By defining joint vertex-time and spectral-frequency spreads, we quantify signal localization across these domains, revealing a trade-off between them. This framework allows us to identify a class of signals with maximal energy concentration in both domains, forming the fundamental atoms for a new joint vertex-time dictionary. This dictionary enhances signal reconstruction under practical constraints, such as incomplete or intermittent data, commonly encountered in sensor and social networks. Numerical experiments on real-world datasets demonstrate the effectiveness of the proposed approach, showing improved reconstruction accuracy and noise robustness compared to existing methods.

A Graph Signal Processing Perspective of Network Multiple Hypothesis Testing with False Discovery Rate Control

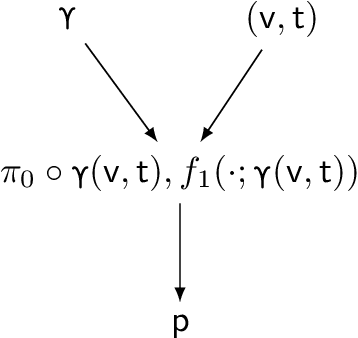
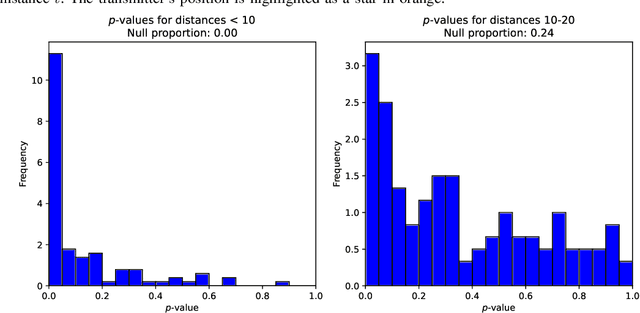
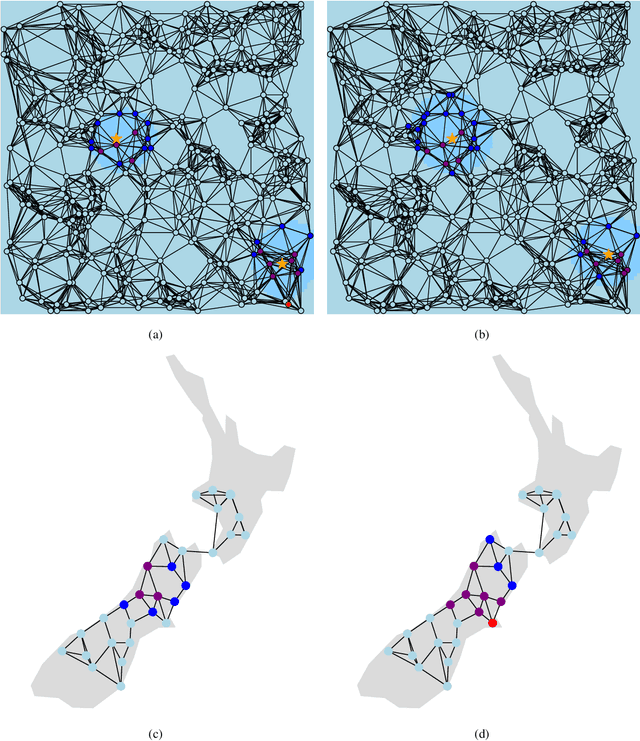
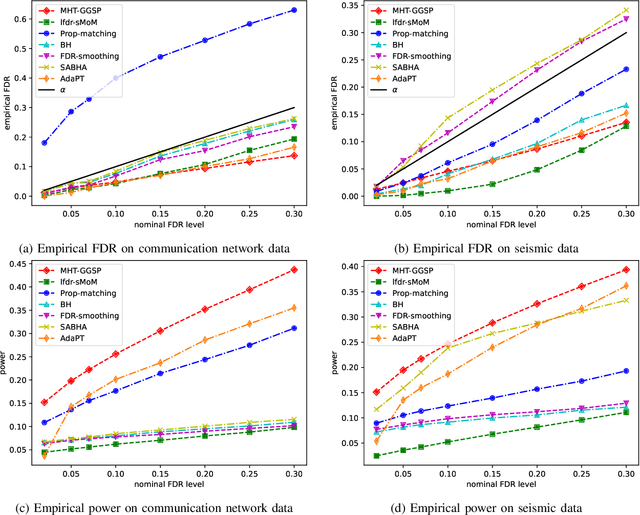
We consider a multiple hypothesis testing problem in a sensor network over the joint spatial-time domain. The sensor network is modeled as a graph, with each vertex representing a sensor and a signal over time associated with each vertex. We assume a hypothesis test and an associated p-value for every sample point in the joint spatial-time domain. Our goal is to determine which points have true alternative hypotheses. By parameterizing the unknown alternative distribution of $p$-values and the prior probabilities of hypotheses being null with a bandlimited generalized graph signal, we can obtain consistent estimates for them. Consequently, we also obtain an estimate of the local false discovery rates (lfdr). We prove that by using a step-up procedure on the estimated lfdr, we can achieve asymptotic false discovery rate control at a pre-determined level. Numerical experiments validate the effectiveness of our approach compared to existing methods.

Unleashing the Potential of Fractional Calculus in Graph Neural Networks with FROND

We introduce the FRactional-Order graph Neural Dynamical network (FROND), a new continuous graph neural network (GNN) framework. Unlike traditional continuous GNNs that rely on integer-order differential equations, FROND employs the Caputo fractional derivative to leverage the non-local properties of fractional calculus. This approach enables the capture of long-term dependencies in feature updates, moving beyond the Markovian update mechanisms in conventional integer-order models and offering enhanced capabilities in graph representation learning. We offer an interpretation of the node feature updating process in FROND from a non-Markovian random walk perspective when the feature updating is particularly governed by a diffusion process. We demonstrate analytically that oversmoothing can be mitigated in this setting. Experimentally, we validate the FROND framework by comparing the fractional adaptations of various established integer-order continuous GNNs, demonstrating their consistently improved performance and underscoring the framework's potential as an effective extension to enhance traditional continuous GNNs. The code is available at \url{https://github.com/zknus/ICLR2024-FROND}.

Online Signed Sampling of Bandlimited Graph Signals

The theory of sampling and recovery of bandlimited graph signals has been extensively studied. However, in many cases, the observation of a signal is quite coarse. For example, users only provide simple comments such as "like" or "dislike" for a product on an e-commerce platform. This is a particular scenario where only the sign information of a graph signal can be measured. In this paper, we are interested in how to sample based on sign information in an online manner, by which the direction of the original graph signal can be estimated. The online signed sampling problem of a graph signal can be formulated as a Markov decision process in a finite horizon. Unfortunately, it is intractable for large size graphs. We propose a low-complexity greedy signed sampling algorithm (GSS) as well as a stopping criterion. Meanwhile, we prove that the objective function is adaptive monotonic and adaptive submodular, so that the performance is close enough to the global optimum with a lower bound. Finally, we demonstrate the effectiveness of the GSS algorithm by both synthesis and realworld data.