Sparse Interpretable Deep Learning with LIES Networks for Symbolic Regression

Symbolic regression (SR) aims to discover closed-form mathematical expressions that accurately describe data, offering interpretability and analytical insight beyond standard black-box models. Existing SR methods often rely on population-based search or autoregressive modeling, which struggle with scalability and symbolic consistency. We introduce LIES (Logarithm, Identity, Exponential, Sine), a fixed neural network architecture with interpretable primitive activations that are optimized to model symbolic expressions. We develop a framework to extract compact formulae from LIES networks by training with an appropriate oversampling strategy and a tailored loss function to promote sparsity and to prevent gradient instability. After training, it applies additional pruning strategies to further simplify the learned expressions into compact formulae. Our experiments on SR benchmarks show that the LIES framework consistently produces sparse and accurate symbolic formulae outperforming all baselines. We also demonstrate the importance of each design component through ablation studies.

Joint Optimization of Primary and Secondary Transforms Using Rate-Distortion Optimized Transform Design

Data-dependent transforms are increasingly being incorporated into next-generation video coding systems such as AVM, a codec under development by the Alliance for Open Media (AOM), and VVC. To circumvent the computational complexities associated with implementing non-separable data-dependent transforms, combinations of separable primary transforms and non-separable secondary transforms have been studied and integrated into video coding standards. These codecs often utilize rate-distortion optimized transforms (RDOT) to ensure that the new transforms complement existing transforms like the DCT and the ADST. In this work, we propose an optimization framework for jointly designing primary and secondary transforms from data through a rate-distortion optimized clustering. Primary transforms are assumed to follow a path-graph model, while secondary transforms are non-separable. We empirically evaluate our proposed approach using AVM residual data and demonstrate that 1) the joint clustering method achieves lower total RD cost in the RDOT design framework, and 2) jointly optimized separable path-graph transforms (SPGT) provide better coding efficiency compared to separable KLTs obtained from the same data.

Rate-Distortion Optimization with Non-Reference Metrics for UGC Compression

Service providers must encode a large volume of noisy videos to meet the demand for user-generated content (UGC) in online video-sharing platforms. However, low-quality UGC challenges conventional codecs based on rate-distortion optimization (RDO) with full-reference metrics (FRMs). While effective for pristine videos, FRMs drive codecs to preserve artifacts when the input is degraded, resulting in suboptimal compression. A more suitable approach used to assess UGC quality is based on non-reference metrics (NRMs). However, RDO with NRMs as a measure of distortion requires an iterative workflow of encoding, decoding, and metric evaluation, which is computationally impractical. This paper overcomes this limitation by linearizing the NRM around the uncompressed video. The resulting cost function enables block-wise bit allocation in the transform domain by estimating the alignment of the quantization error with the gradient of the NRM. To avoid large deviations from the input, we add sum of squared errors (SSE) regularization. We derive expressions for both the SSE regularization parameter and the Lagrangian, akin to the relationship used for SSE-RDO. Experiments with images and videos show bitrate savings of more than 30\% over SSE-RDO using the target NRM, with no decoder complexity overhead and minimal encoder complexity increase.

Image Coding for Machines via Feature-Preserving Rate-Distortion Optimization

Many images and videos are primarily processed by computer vision algorithms, involving only occasional human inspection. When this content requires compression before processing, e.g., in distributed applications, coding methods must optimize for both visual quality and downstream task performance. We first show that, given the features obtained from the original and the decoded images, an approach to reduce the effect of compression on a task loss is to perform rate-distortion optimization (RDO) using the distance between features as a distortion metric. However, optimizing directly such a rate-distortion trade-off requires an iterative workflow of encoding, decoding, and feature evaluation for each coding parameter, which is computationally impractical. We address this problem by simplifying the RDO formulation to make the distortion term computable using block-based encoders. We first apply Taylor's expansion to the feature extractor, recasting the feature distance as a quadratic metric with the Jacobian matrix of the neural network. Then, we replace the linearized metric with a block-wise approximation, which we call input-dependent squared error (IDSE). To reduce computational complexity, we approximate IDSE using Jacobian sketches. The resulting loss can be evaluated block-wise in the transform domain and combined with the sum of squared errors (SSE) to address both visual quality and computer vision performance. Simulations with AVC across multiple feature extractors and downstream neural networks show up to 10% bit-rate savings for the same computer vision accuracy compared to RDO based on SSE, with no decoder complexity overhead and just a 7% encoder complexity increase.

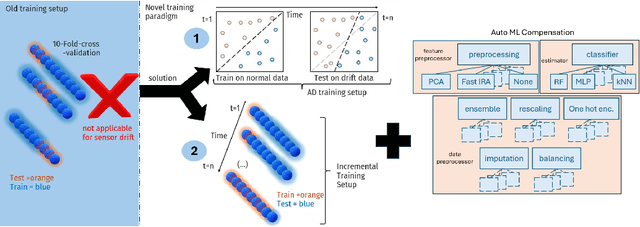
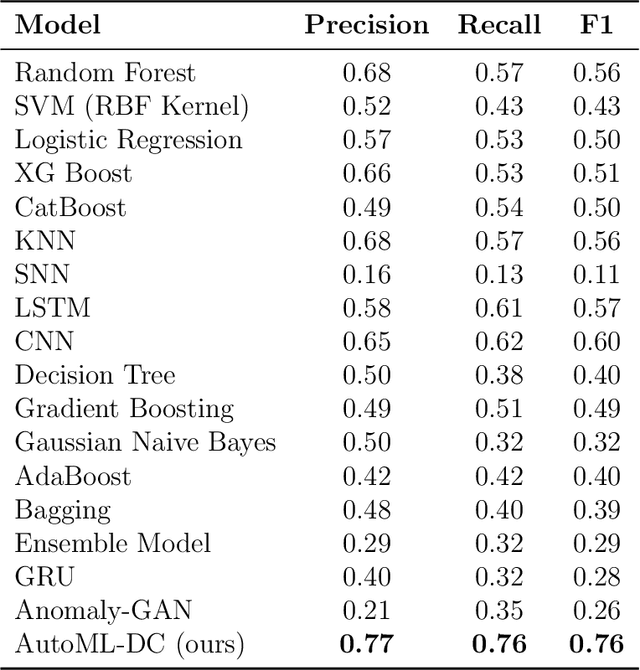
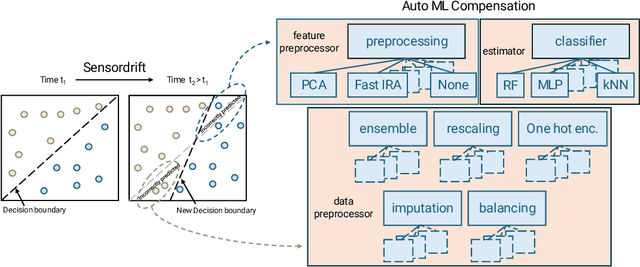
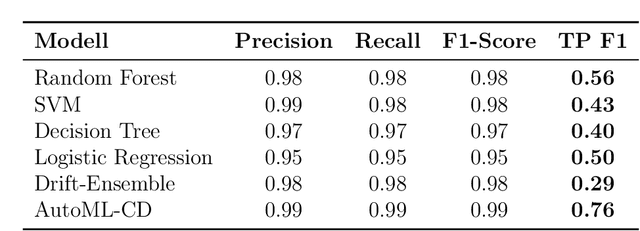
AutoML for Multi-Class Anomaly Compensation of Sensor Drift

Addressing sensor drift is essential in industrial measurement systems, where precise data output is necessary for maintaining accuracy and reliability in monitoring processes, as it progressively degrades the performance of machine learning models over time. Our findings indicate that the standard cross-validation method used in existing model training overestimates performance by inadequately accounting for drift. This is primarily because typical cross-validation techniques allow data instances to appear in both training and testing sets, thereby distorting the accuracy of the predictive evaluation. As a result, these models are unable to precisely predict future drift effects, compromising their ability to generalize and adapt to evolving data conditions. This paper presents two solutions: (1) a novel sensor drift compensation learning paradigm for validating models, and (2) automated machine learning (AutoML) techniques to enhance classification performance and compensate sensor drift. By employing strategies such as data balancing, meta-learning, automated ensemble learning, hyperparameter optimization, feature selection, and boosting, our AutoML-DC (Drift Compensation) model significantly improves classification performance against sensor drift. AutoML-DC further adapts effectively to varying drift severities.

Towards joint graph learning and sampling set selection from data

We explore the problem of sampling graph signals in scenarios where the graph structure is not predefined and must be inferred from data. In this scenario, existing approaches rely on a two-step process, where a graph is learned first, followed by sampling. More generally, graph learning and graph signal sampling have been studied as two independent problems in the literature. This work provides a foundational step towards jointly optimizing the graph structure and sampling set. Our main contribution, Vertex Importance Sampling (VIS), is to show that the sampling set can be effectively determined from the vertex importance (node weights) obtained from graph learning. We further propose Vertex Importance Sampling with Repulsion (VISR), a greedy algorithm where spatially -separated "important" nodes are selected to ensure better reconstruction. Empirical results on simulated data show that sampling using VIS and VISR leads to competitive reconstruction performance and lower complexity than the conventional two-step approach of graph learning followed by graph sampling.

Towards joint graph and sampling set selection from data

We explore the problem of sampling graph signals in scenarios where the graph structure is not predefined and must be inferred from data. In this scenario, existing approaches rely on a two-step process, where a graph is learned first, followed by sampling. More generally, graph learning and graph signal sampling have been studied as two independent problems in the literature. This work provides a foundational step towards jointly optimizing the graph structure and sampling set. Our main contribution, Vertex Importance Sampling (VIS), is to show that the sampling set can be effectively determined from the vertex importance (node weights) obtained from graph learning. We further propose Vertex Importance Sampling with Repulsion (VISR), a greedy algorithm where spatially -separated "important" nodes are selected to ensure better reconstruction. Empirical results on simulated data show that sampling using VIS and VISR leads to competitive reconstruction performance and lower complexity than the conventional two-step approach of graph learning followed by graph sampling.

Variable-size Symmetry-based Graph Fourier Transforms for image compression

Modern compression systems use linear transformations in their encoding and decoding processes, with transforms providing compact signal representations. While multiple data-dependent transforms for image/video coding can adapt to diverse statistical characteristics, assembling large datasets to learn each transform is challenging. Also, the resulting transforms typically lack fast implementation, leading to significant computational costs. Thus, despite many papers proposing new transform families, the most recent compression standards predominantly use traditional separable sinusoidal transforms. This paper proposes integrating a new family of Symmetry-based Graph Fourier Transforms (SBGFTs) of variable sizes into a coding framework, focusing on the extension from our previously introduced 8x8 SBGFTs to the general case of NxN grids. SBGFTs are non-separable transforms that achieve sparse signal representation while maintaining low computational complexity thanks to their symmetry properties. Their design is based on our proposed algorithm, which generates symmetric graphs on the grid by adding specific symmetrical connections between nodes and does not require any data-dependent adaptation. Furthermore, for video intra-frame coding, we exploit the correlations between optimal graphs and prediction modes to reduce the cardinality of the transform sets, thus proposing a low-complexity framework. Experiments show that SBGFTs outperform the primary transforms integrated in the explicit Multiple Transform Selection (MTS) used in the latest VVC intra-coding, providing a bit rate saving percentage of 6.23%, with only a marginal increase in average complexity. A MATLAB implementation of the proposed algorithm is available online at [1].

Color-Guided Flying Pixel Correction in Depth Images

We present a novel method to correct flying pixels within data captured by Time-of-flight (ToF) sensors. Flying pixel (FP) artifacts occur when signals from foreground and background objects reach the same sensor pixel, leading to a confident yet incorrect depth estimation in space - floating between two objects. Commercial RGB-D cameras have a complementary setup consisting of ToF sensors to capture depth in addition to RGB cameras. We propose a novel method to correct FPs by leveraging the aligned RGB and depth image in such RGB-D cameras to estimate the true depth values of FPs. Our method defines a 3D neighborhood around each point, representing a "field of view" that mirrors the acquisition process of ToF cameras. We propose a two-step iterative correction algorithm in which the FPs are first identified. Then, we estimate the true depth value of FPs by solving a least-squares optimization problem. Experimental results show that our proposed algorithm estimates the depth value of FPs as accurately as other algorithms in the literature.

Graph-based Scalable Sampling of 3D Point Cloud Attributes

3D Point clouds (PCs) are commonly used to represent 3D scenes. They can have millions of points, making subsequent downstream tasks such as compression and streaming computationally expensive. PC sampling (selecting a subset of points) can be used to reduce complexity. Existing PC sampling algorithms focus on preserving geometry features and often do not scale to handle large PCs. In this work, we develop scalable graph-based sampling algorithms for PC color attributes, assuming the full geometry is available. Our sampling algorithms are optimized for a signal reconstruction method that minimizes the graph Laplacian quadratic form. We first develop a global sampling algorithm that can be applied to PCs with millions of points by exploiting sparsity and sampling rate adaptive parameter selection. Further, we propose a block-based sampling strategy where each block is sampled independently. We show that sampling the corresponding sub-graphs with optimally chosen self-loop weights (node weights) will produce a sampling set that approximates the results of global sampling while reducing complexity by an order of magnitude. Our empirical results on two large PC datasets show that our algorithms outperform the existing fast PC subsampling techniques (uniform and geometry feature preserving random sampling) by 2dB. Our algorithm is up to 50 times faster than existing graph signal sampling algorithms while providing better reconstruction accuracy. Finally, we illustrate the efficacy of PC attribute sampling within a compression scenario, showing that pre-compression sampling of PC attributes can lower the bitrate by 11% while having minimal effect on reconstruction.