Rate-Distortion Optimization for Ensembles of Non-Reference Metrics

Non-reference metrics (NRMs) can assess the visual quality of images and videos without a reference, making them well-suited for the evaluation of user-generated content. Nonetheless, rate-distortion optimization (RDO) in video coding is still mainly driven by full-reference metrics, such as the sum of squared errors, which treat the input as an ideal target. A way to incorporate NRMs into RDO is through linearization (LNRM), where the gradient of the NRM with respect to the input guides bit allocation. While this strategy improves the quality predicted by some metrics, we show that it can yield limited gains or degradations when evaluated with other NRMs. We argue that NRMs are highly non-linear predictors with locally unstable gradients that can compromise the quality of the linearization; furthermore, optimizing a single metric may exploit model-specific biases that do not generalize across quality estimators. Motivated by this observation, we extend the LNRM framework to optimize ensembles of NRMs and, to further improve robustness, we introduce a smoothing-based formulation that stabilizes NRM gradients prior to linearization. Our framework is well-suited to hybrid codecs, and we advocate for its use with overfitted codecs, where it avoids iterative evaluations and backpropagation of neural network-based NRMs, reducing encoder complexity relative to direct NRM optimization. We validate the proposed approach on AVC and Cool-chic, using the YouTube UGC dataset. Experiments demonstrate consistent bitrate savings across multiple NRMs with no decoder complexity overhead and, for Cool-chic, a substantial reduction in encoding runtime compared to direct NRM optimization.

Wrapper-Aware Rate-Distortion Optimization in Feature Coding for Machines

Feature coding for machines (FCM) is a lossy compression paradigm for split-inference. The transmitter encodes the outputs of the first part of a neural network before sending them to the receiver for completing the inference. Practical FCM methods ``sandwich'' a traditional codec between pre- and post-processing neural networks, called wrappers, to make features easier to compress using video codecs. Since traditional codecs are non-differentiable, the wrappers are trained using a proxy codec, which is later replaced by a standard codec after training. These codecs perform rate-distortion optimization (RDO) based on the sum of squared errors (SSE). Because the RDO does not consider the post-processing wrapper, the inner codec can invest bits in preserving information that the post-processing later discards. In this paper, we modify the bit-allocation in the inner codec via a wrapper-aware weighted SSE metric. To make wrapper-aware RDO (WA-RDO) practical for FCM, we propose: 1) temporal reuse of weights across a group of pictures and 2) fixed, architecture- and task-dependent weights trained offline. Under MPEG test conditions, our methods implemented on HEVC match the VVC-based FCM state-of-the-art, effectively bridging a codec generation gap with minimal runtime overhead relative to SSE-RDO HEVC.

Rate-Distortion Optimization with Non-Reference Metrics for UGC Compression

Service providers must encode a large volume of noisy videos to meet the demand for user-generated content (UGC) in online video-sharing platforms. However, low-quality UGC challenges conventional codecs based on rate-distortion optimization (RDO) with full-reference metrics (FRMs). While effective for pristine videos, FRMs drive codecs to preserve artifacts when the input is degraded, resulting in suboptimal compression. A more suitable approach used to assess UGC quality is based on non-reference metrics (NRMs). However, RDO with NRMs as a measure of distortion requires an iterative workflow of encoding, decoding, and metric evaluation, which is computationally impractical. This paper overcomes this limitation by linearizing the NRM around the uncompressed video. The resulting cost function enables block-wise bit allocation in the transform domain by estimating the alignment of the quantization error with the gradient of the NRM. To avoid large deviations from the input, we add sum of squared errors (SSE) regularization. We derive expressions for both the SSE regularization parameter and the Lagrangian, akin to the relationship used for SSE-RDO. Experiments with images and videos show bitrate savings of more than 30\% over SSE-RDO using the target NRM, with no decoder complexity overhead and minimal encoder complexity increase.

Image Coding for Machines via Feature-Preserving Rate-Distortion Optimization

Many images and videos are primarily processed by computer vision algorithms, involving only occasional human inspection. When this content requires compression before processing, e.g., in distributed applications, coding methods must optimize for both visual quality and downstream task performance. We first show that, given the features obtained from the original and the decoded images, an approach to reduce the effect of compression on a task loss is to perform rate-distortion optimization (RDO) using the distance between features as a distortion metric. However, optimizing directly such a rate-distortion trade-off requires an iterative workflow of encoding, decoding, and feature evaluation for each coding parameter, which is computationally impractical. We address this problem by simplifying the RDO formulation to make the distortion term computable using block-based encoders. We first apply Taylor's expansion to the feature extractor, recasting the feature distance as a quadratic metric with the Jacobian matrix of the neural network. Then, we replace the linearized metric with a block-wise approximation, which we call input-dependent squared error (IDSE). To reduce computational complexity, we approximate IDSE using Jacobian sketches. The resulting loss can be evaluated block-wise in the transform domain and combined with the sum of squared errors (SSE) to address both visual quality and computer vision performance. Simulations with AVC across multiple feature extractors and downstream neural networks show up to 10% bit-rate savings for the same computer vision accuracy compared to RDO based on SSE, with no decoder complexity overhead and just a 7% encoder complexity increase.

Fast DCT+: A Family of Fast Transforms Based on Rank-One Updates of the Path Graph

This paper develops fast graph Fourier transform (GFT) algorithms with O(n log n) runtime complexity for rank-one updates of the path graph. We first show that several commonly-used audio and video coding transforms belong to this class of GFTs, which we denote by DCT+. Next, starting from an arbitrary generalized graph Laplacian and using rank-one perturbation theory, we provide a factorization for the GFT after perturbation. This factorization is our central result and reveals a progressive structure: we first apply the unperturbed Laplacian's GFT and then multiply the result by a Cauchy matrix. By specializing this decomposition to path graphs and exploiting the properties of Cauchy matrices, we show that Fast DCT+ algorithms exist. We also demonstrate that progressivity can speed up computations in applications involving multiple transforms related by rank-one perturbations (e.g., video coding) when combined with pruning strategies. Our results can be extended to other graphs and rank-k perturbations. Runtime analyses show that Fast DCT+ provides computational gains over the naive method for graph sizes larger than 64, with runtime approximately equal to that of 8 DCTs.

Image Coding via Perceptually Inspired Graph Learning

Most codec designs rely on the mean squared error (MSE) as a fidelity metric in rate-distortion optimization, which allows to choose the optimal parameters in the transform domain but may fail to reflect perceptual quality. Alternative distortion metrics, such as the structural similarity index (SSIM), can be computed only pixel-wise, so they cannot be used directly for transform-domain bit allocation. Recently, the irregularity-aware graph Fourier transform (IAGFT) emerged as a means to include pixel-wise perceptual information in the transform design. This paper extends this idea by also learning a graph (and corresponding transform) for sets of blocks that share similar perceptual characteristics and are observed to differ statistically, leading to different learned graphs. We demonstrate the effectiveness of our method with both SSIM- and saliency-based criteria. We also propose a framework to derive separable transforms, including separable IAGFTs. An empirical evaluation based on the 5th CLIC dataset shows that our approach achieves improvements in terms of MS-SSIM with respect to existing methods.

PRNU Emphasis: a Generalization of the Multiplicative Model

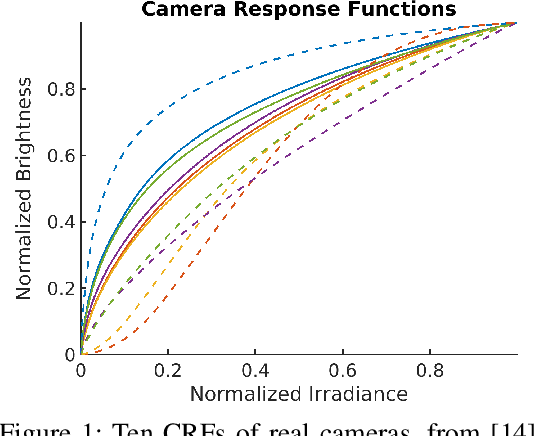
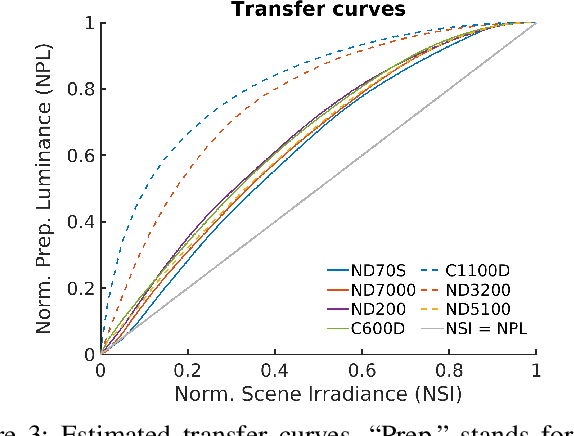
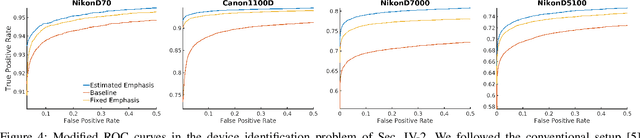
The photoresponse non-uniformity (PRNU) is a camera-specific pattern, widely adopted to solve multimedia forensics problems such as device identification or forgery detection. The theoretical analysis of this fingerprint customarily relies on a multiplicative model for the denoising residuals. This setup assumes that the nonlinear mapping from the scene irradiance to the preprocessed luminance, that is, the composition of the Camera Response Function (CRF) with the optical and digital preprocessing pipelines, is a gamma correction. Yet, this assumption seldom holds in practice. In this letter, we improve the multiplicative model by including the influence of this nonlinear mapping on the denoising residuals. We also propose a method to estimate this effect. Results evidence that the response of typical cameras deviates from a gamma correction. Experimental device identification with our model increases the TPR by a $4.93\, \%$ on average for a fixed FPR of $0.01$.