Eduardo Pavez
Wrapper-Aware Rate-Distortion Optimization in Feature Coding for Machines
Jan 29, 2026Abstract:Feature coding for machines (FCM) is a lossy compression paradigm for split-inference. The transmitter encodes the outputs of the first part of a neural network before sending them to the receiver for completing the inference. Practical FCM methods ``sandwich'' a traditional codec between pre- and post-processing neural networks, called wrappers, to make features easier to compress using video codecs. Since traditional codecs are non-differentiable, the wrappers are trained using a proxy codec, which is later replaced by a standard codec after training. These codecs perform rate-distortion optimization (RDO) based on the sum of squared errors (SSE). Because the RDO does not consider the post-processing wrapper, the inner codec can invest bits in preserving information that the post-processing later discards. In this paper, we modify the bit-allocation in the inner codec via a wrapper-aware weighted SSE metric. To make wrapper-aware RDO (WA-RDO) practical for FCM, we propose: 1) temporal reuse of weights across a group of pictures and 2) fixed, architecture- and task-dependent weights trained offline. Under MPEG test conditions, our methods implemented on HEVC match the VVC-based FCM state-of-the-art, effectively bridging a codec generation gap with minimal runtime overhead relative to SSE-RDO HEVC.
Region-Adaptive Learned Hierarchical Encoding for 3D Gaussian Splatting Data
Oct 26, 2025
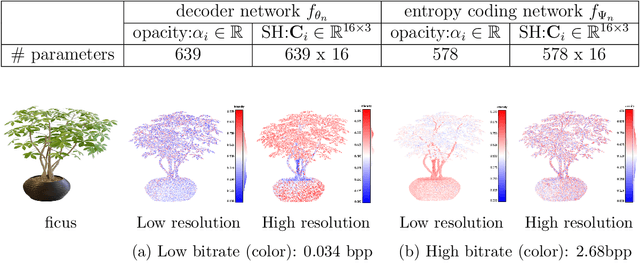
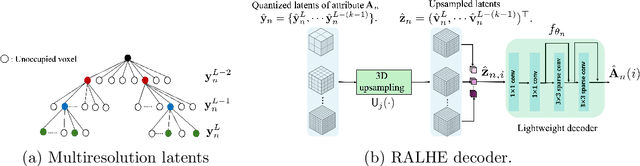

Abstract:We introduce Region-Adaptive Learned Hierarchical Encoding (RALHE) for 3D Gaussian Splatting (3DGS) data. While 3DGS has recently become popular for novel view synthesis, the size of trained models limits its deployment in bandwidth-constrained applications such as volumetric media streaming. To address this, we propose a learned hierarchical latent representation that builds upon the principles of "overfitted" learned image compression (e.g., Cool-Chic and C3) to efficiently encode 3DGS attributes. Unlike images, 3DGS data have irregular spatial distributions of Gaussians (geometry) and consist of multiple attributes (signals) defined on the irregular geometry. Our codec is designed to account for these differences between images and 3DGS. Specifically, we leverage the octree structure of the voxelized 3DGS geometry to obtain a hierarchical multi-resolution representation. Our approach overfits latents to each Gaussian attribute under a global rate constraint. These latents are decoded independently through a lightweight decoder network. To estimate the bitrate during training, we employ an autoregressive probability model that leverages octree-derived contexts from the 3D point structure. The multi-resolution latents, decoder, and autoregressive entropy coding networks are jointly optimized for each Gaussian attribute. Experiments demonstrate that the proposed RALHE compression framework achieves a rendering PSNR gain of up to 2dB at low bitrates (less than 1 MB) compared to the baseline 3DGS compression methods.
Joint Optimization of Primary and Secondary Transforms Using Rate-Distortion Optimized Transform Design
May 21, 2025



Abstract:Data-dependent transforms are increasingly being incorporated into next-generation video coding systems such as AVM, a codec under development by the Alliance for Open Media (AOM), and VVC. To circumvent the computational complexities associated with implementing non-separable data-dependent transforms, combinations of separable primary transforms and non-separable secondary transforms have been studied and integrated into video coding standards. These codecs often utilize rate-distortion optimized transforms (RDOT) to ensure that the new transforms complement existing transforms like the DCT and the ADST. In this work, we propose an optimization framework for jointly designing primary and secondary transforms from data through a rate-distortion optimized clustering. Primary transforms are assumed to follow a path-graph model, while secondary transforms are non-separable. We empirically evaluate our proposed approach using AVM residual data and demonstrate that 1) the joint clustering method achieves lower total RD cost in the RDOT design framework, and 2) jointly optimized separable path-graph transforms (SPGT) provide better coding efficiency compared to separable KLTs obtained from the same data.
Rate-Distortion Optimization with Non-Reference Metrics for UGC Compression
May 21, 2025Abstract:Service providers must encode a large volume of noisy videos to meet the demand for user-generated content (UGC) in online video-sharing platforms. However, low-quality UGC challenges conventional codecs based on rate-distortion optimization (RDO) with full-reference metrics (FRMs). While effective for pristine videos, FRMs drive codecs to preserve artifacts when the input is degraded, resulting in suboptimal compression. A more suitable approach used to assess UGC quality is based on non-reference metrics (NRMs). However, RDO with NRMs as a measure of distortion requires an iterative workflow of encoding, decoding, and metric evaluation, which is computationally impractical. This paper overcomes this limitation by linearizing the NRM around the uncompressed video. The resulting cost function enables block-wise bit allocation in the transform domain by estimating the alignment of the quantization error with the gradient of the NRM. To avoid large deviations from the input, we add sum of squared errors (SSE) regularization. We derive expressions for both the SSE regularization parameter and the Lagrangian, akin to the relationship used for SSE-RDO. Experiments with images and videos show bitrate savings of more than 30\% over SSE-RDO using the target NRM, with no decoder complexity overhead and minimal encoder complexity increase.
Image Coding for Machines via Feature-Preserving Rate-Distortion Optimization
Apr 03, 2025



Abstract:Many images and videos are primarily processed by computer vision algorithms, involving only occasional human inspection. When this content requires compression before processing, e.g., in distributed applications, coding methods must optimize for both visual quality and downstream task performance. We first show that, given the features obtained from the original and the decoded images, an approach to reduce the effect of compression on a task loss is to perform rate-distortion optimization (RDO) using the distance between features as a distortion metric. However, optimizing directly such a rate-distortion trade-off requires an iterative workflow of encoding, decoding, and feature evaluation for each coding parameter, which is computationally impractical. We address this problem by simplifying the RDO formulation to make the distortion term computable using block-based encoders. We first apply Taylor's expansion to the feature extractor, recasting the feature distance as a quadratic metric with the Jacobian matrix of the neural network. Then, we replace the linearized metric with a block-wise approximation, which we call input-dependent squared error (IDSE). To reduce computational complexity, we approximate IDSE using Jacobian sketches. The resulting loss can be evaluated block-wise in the transform domain and combined with the sum of squared errors (SSE) to address both visual quality and computer vision performance. Simulations with AVC across multiple feature extractors and downstream neural networks show up to 10% bit-rate savings for the same computer vision accuracy compared to RDO based on SSE, with no decoder complexity overhead and just a 7% encoder complexity increase.
Towards joint graph learning and sampling set selection from data
Dec 16, 2024


Abstract:We explore the problem of sampling graph signals in scenarios where the graph structure is not predefined and must be inferred from data. In this scenario, existing approaches rely on a two-step process, where a graph is learned first, followed by sampling. More generally, graph learning and graph signal sampling have been studied as two independent problems in the literature. This work provides a foundational step towards jointly optimizing the graph structure and sampling set. Our main contribution, Vertex Importance Sampling (VIS), is to show that the sampling set can be effectively determined from the vertex importance (node weights) obtained from graph learning. We further propose Vertex Importance Sampling with Repulsion (VISR), a greedy algorithm where spatially -separated "important" nodes are selected to ensure better reconstruction. Empirical results on simulated data show that sampling using VIS and VISR leads to competitive reconstruction performance and lower complexity than the conventional two-step approach of graph learning followed by graph sampling.
Towards joint graph and sampling set selection from data
Dec 12, 2024


Abstract:We explore the problem of sampling graph signals in scenarios where the graph structure is not predefined and must be inferred from data. In this scenario, existing approaches rely on a two-step process, where a graph is learned first, followed by sampling. More generally, graph learning and graph signal sampling have been studied as two independent problems in the literature. This work provides a foundational step towards jointly optimizing the graph structure and sampling set. Our main contribution, Vertex Importance Sampling (VIS), is to show that the sampling set can be effectively determined from the vertex importance (node weights) obtained from graph learning. We further propose Vertex Importance Sampling with Repulsion (VISR), a greedy algorithm where spatially -separated "important" nodes are selected to ensure better reconstruction. Empirical results on simulated data show that sampling using VIS and VISR leads to competitive reconstruction performance and lower complexity than the conventional two-step approach of graph learning followed by graph sampling.
Color-Guided Flying Pixel Correction in Depth Images
Oct 10, 2024



Abstract:We present a novel method to correct flying pixels within data captured by Time-of-flight (ToF) sensors. Flying pixel (FP) artifacts occur when signals from foreground and background objects reach the same sensor pixel, leading to a confident yet incorrect depth estimation in space - floating between two objects. Commercial RGB-D cameras have a complementary setup consisting of ToF sensors to capture depth in addition to RGB cameras. We propose a novel method to correct FPs by leveraging the aligned RGB and depth image in such RGB-D cameras to estimate the true depth values of FPs. Our method defines a 3D neighborhood around each point, representing a "field of view" that mirrors the acquisition process of ToF cameras. We propose a two-step iterative correction algorithm in which the FPs are first identified. Then, we estimate the true depth value of FPs by solving a least-squares optimization problem. Experimental results show that our proposed algorithm estimates the depth value of FPs as accurately as other algorithms in the literature.
Graph-based Scalable Sampling of 3D Point Cloud Attributes
Oct 01, 2024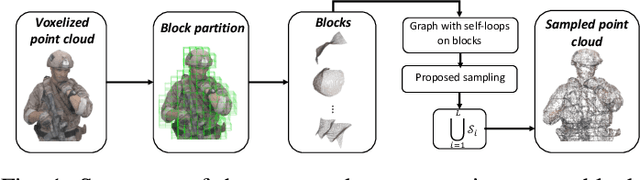
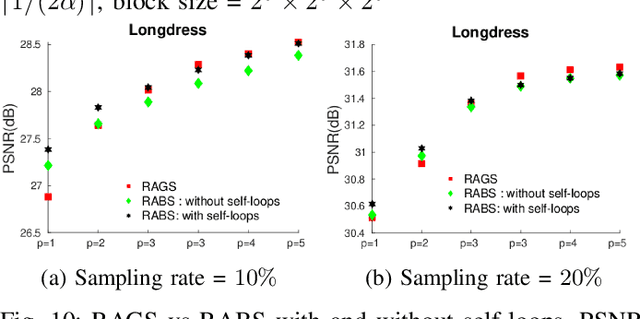
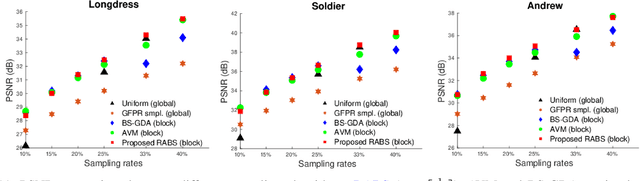
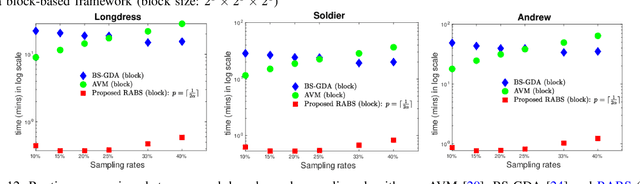
Abstract:3D Point clouds (PCs) are commonly used to represent 3D scenes. They can have millions of points, making subsequent downstream tasks such as compression and streaming computationally expensive. PC sampling (selecting a subset of points) can be used to reduce complexity. Existing PC sampling algorithms focus on preserving geometry features and often do not scale to handle large PCs. In this work, we develop scalable graph-based sampling algorithms for PC color attributes, assuming the full geometry is available. Our sampling algorithms are optimized for a signal reconstruction method that minimizes the graph Laplacian quadratic form. We first develop a global sampling algorithm that can be applied to PCs with millions of points by exploiting sparsity and sampling rate adaptive parameter selection. Further, we propose a block-based sampling strategy where each block is sampled independently. We show that sampling the corresponding sub-graphs with optimally chosen self-loop weights (node weights) will produce a sampling set that approximates the results of global sampling while reducing complexity by an order of magnitude. Our empirical results on two large PC datasets show that our algorithms outperform the existing fast PC subsampling techniques (uniform and geometry feature preserving random sampling) by 2dB. Our algorithm is up to 50 times faster than existing graph signal sampling algorithms while providing better reconstruction accuracy. Finally, we illustrate the efficacy of PC attribute sampling within a compression scenario, showing that pre-compression sampling of PC attributes can lower the bitrate by 11% while having minimal effect on reconstruction.
Graph-Based Signal Sampling with Adaptive Subspace Reconstruction for Spatially-Irregular Sensor Data
Sep 14, 2024



Abstract:Choosing an appropriate frequency definition and norm is critical in graph signal sampling and reconstruction. Most previous works define frequencies based on the spectral properties of the graph and use the same frequency definition and $\ell_2$-norm for optimization for all sampling sets. Our previous work demonstrated that using a sampling set-adaptive norm and frequency definition can address challenges in classical bandlimited approximation, particularly with model mismatches and irregularly distributed data. In this work, we propose a method for selecting sampling sets tailored to the sampling set adaptive GFT-based interpolation. When the graph models the inverse covariance of the data, we show that this adaptive GFT enables localizing the bandlimited model mismatch error to high frequencies, and the spectral folding property allows us to track this error in reconstruction. Based on this, we propose a sampling set selection algorithm to minimize the worst-case bandlimited model mismatch error. We consider partitioning the sensors in a sensor network sampling a continuous spatial process as an application. Our experiments show that sampling and reconstruction using sampling set adaptive GFT significantly outperform methods that used fixed GFTs and bandwidth-based criterion.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge