Graph-Based Signal Sampling with Adaptive Subspace Reconstruction for Spatially-Irregular Sensor Data

Choosing an appropriate frequency definition and norm is critical in graph signal sampling and reconstruction. Most previous works define frequencies based on the spectral properties of the graph and use the same frequency definition and $\ell_2$-norm for optimization for all sampling sets. Our previous work demonstrated that using a sampling set-adaptive norm and frequency definition can address challenges in classical bandlimited approximation, particularly with model mismatches and irregularly distributed data. In this work, we propose a method for selecting sampling sets tailored to the sampling set adaptive GFT-based interpolation. When the graph models the inverse covariance of the data, we show that this adaptive GFT enables localizing the bandlimited model mismatch error to high frequencies, and the spectral folding property allows us to track this error in reconstruction. Based on this, we propose a sampling set selection algorithm to minimize the worst-case bandlimited model mismatch error. We consider partitioning the sensors in a sensor network sampling a continuous spatial process as an application. Our experiments show that sampling and reconstruction using sampling set adaptive GFT significantly outperform methods that used fixed GFTs and bandwidth-based criterion.

Irregularity-Aware Bandlimited Approximation for Graph Signal Iinterpolation

In most work to date, graph signal sampling and reconstruction algorithms are intrinsically tied to graph properties, assuming bandlimitedness and optimal sampling set choices. However, practical scenarios often defy these assumptions, leading to suboptimal performance. In the context of sampling and reconstruction, graph irregularities lead to varying contributions from sampled nodes for interpolation and differing levels of reliability for interpolated nodes. The existing GFT-based methods in the literature make bandlimited signal approximations without taking into account graph irregularities and the relative significance of nodes, resulting in suboptimal reconstruction performance under various mismatch conditions. In this paper, we leverage the GFT equipped with a specific inner product to address graph irregularities and account for the relative importance of nodes during the bandlimited signal approximation and interpolation process. Empirical evidence demonstrates that the proposed method outperforms other GFT-based approaches for bandlimited signal interpolation in challenging scenarios, such as sampling sets selected independently of the underlying graph, low sampling rates, and high noise levels.

WLS Design of ARMA Graph Filters using Iterative Second-Order Cone Programming

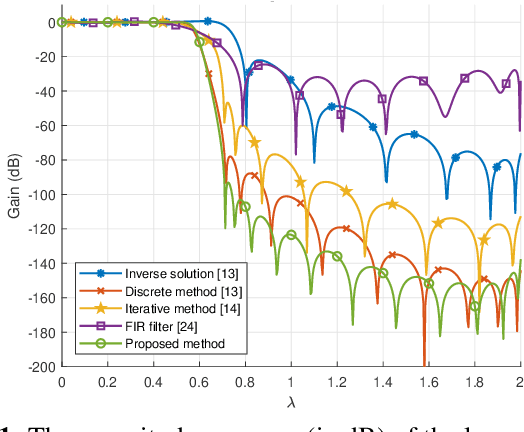
We propose a weighted least-square (WLS) method to design autoregressive moving average (ARMA) graph filters. We first express the WLS design problem as a numerically-stable optimization problem using Chebyshev polynomial bases. We then formulate the optimization problem with a nonconvex objective function and linear constraints for stability. We employ a relaxation technique and convert the nonconvex optimization problem into an iterative second-order cone programming problem. Experimental results confirm that ARMA graph filters designed using the proposed WLS method have significantly improved frequency responses compared to those designed using previously proposed WLS design methods.