WLS Design of ARMA Graph Filters using Iterative Second-Order Cone Programming

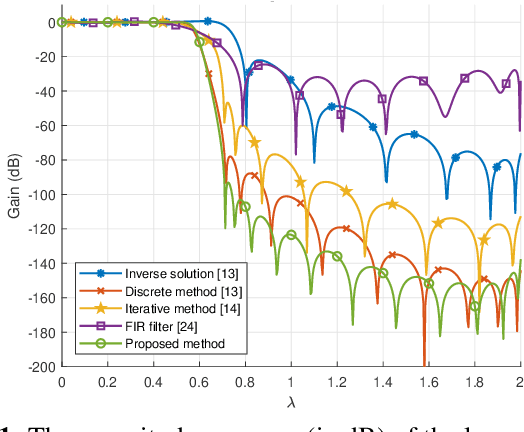
We propose a weighted least-square (WLS) method to design autoregressive moving average (ARMA) graph filters. We first express the WLS design problem as a numerically-stable optimization problem using Chebyshev polynomial bases. We then formulate the optimization problem with a nonconvex objective function and linear constraints for stability. We employ a relaxation technique and convert the nonconvex optimization problem into an iterative second-order cone programming problem. Experimental results confirm that ARMA graph filters designed using the proposed WLS method have significantly improved frequency responses compared to those designed using previously proposed WLS design methods.