Joint Optimization of Primary and Secondary Transforms Using Rate-Distortion Optimized Transform Design

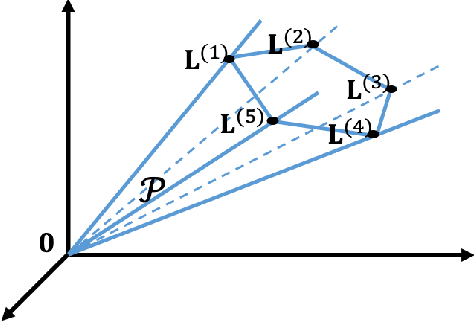
Data-dependent transforms are increasingly being incorporated into next-generation video coding systems such as AVM, a codec under development by the Alliance for Open Media (AOM), and VVC. To circumvent the computational complexities associated with implementing non-separable data-dependent transforms, combinations of separable primary transforms and non-separable secondary transforms have been studied and integrated into video coding standards. These codecs often utilize rate-distortion optimized transforms (RDOT) to ensure that the new transforms complement existing transforms like the DCT and the ADST. In this work, we propose an optimization framework for jointly designing primary and secondary transforms from data through a rate-distortion optimized clustering. Primary transforms are assumed to follow a path-graph model, while secondary transforms are non-separable. We empirically evaluate our proposed approach using AVM residual data and demonstrate that 1) the joint clustering method achieves lower total RD cost in the RDOT design framework, and 2) jointly optimized separable path-graph transforms (SPGT) provide better coding efficiency compared to separable KLTs obtained from the same data.

Standard compliant video coding using low complexity, switchable neural wrappers

The proliferation of high resolution videos posts great storage and bandwidth pressure on cloud video services, driving the development of next-generation video codecs. Despite great progress made in neural video coding, existing approaches are still far from economical deployment considering the complexity and rate-distortion performance tradeoff. To clear the roadblocks for neural video coding, in this paper we propose a new framework featuring standard compatibility, high performance, and low decoding complexity. We employ a set of jointly optimized neural pre- and post-processors, wrapping a standard video codec, to encode videos at different resolutions. The rate-distorion optimal downsampling ratio is signaled to the decoder at the per-sequence level for each target rate. We design a low complexity neural post-processor architecture that can handle different upsampling ratios. The change of resolution exploits the spatial redundancy in high-resolution videos, while the neural wrapper further achieves rate-distortion performance improvement through end-to-end optimization with a codec proxy. Our light-weight post-processor architecture has a complexity of 516 MACs / pixel, and achieves 9.3% BD-Rate reduction over VVC on the UVG dataset, and 6.4% on AOM CTC Class A1. Our approach has the potential to further advance the performance of the latest video coding standards using neural processing with minimal added complexity.

DCT and DST Filtering with Sparse Graph Operators

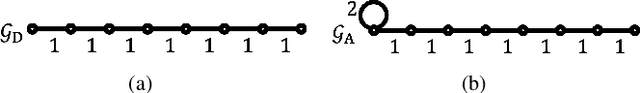
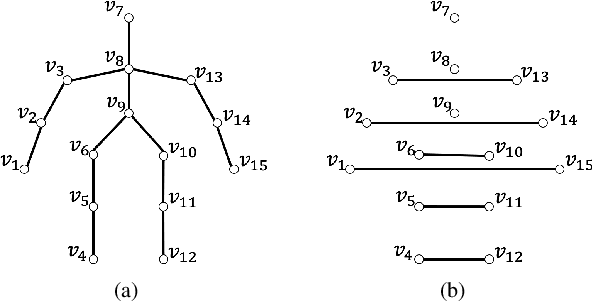
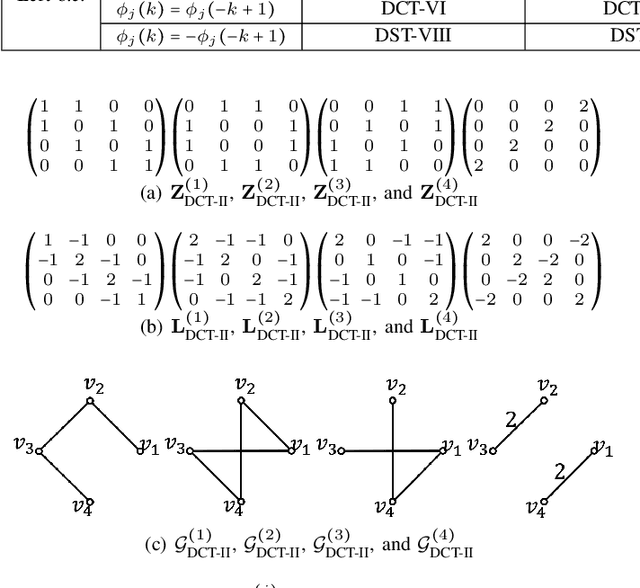
Graph filtering is a fundamental tool in graph signal processing. Polynomial graph filters (PGFs), defined as polynomials of a fundamental graph operator, can be implemented in the vertex domain, and usually have a lower complexity than frequency domain filter implementations. In this paper, we focus on the design of filters for graphs with graph Fourier transform (GFT) corresponding to a discrete trigonometric transform (DTT), i.e., one of 8 types of discrete cosine transforms (DCT) and 8 discrete sine transforms (DST). In this case, we show that multiple sparse graph operators can be identified, which allows us to propose a generalization of PGF design: multivariate polynomial graph filter (MPGF). First, for the widely used DCT-II (type-2 DCT), we characterize a set of sparse graph operators that share the DCT-II matrix as their common eigenvector matrix. This set contains the well-known connected line graph. These sparse operators can be viewed as graph filters operating in the DCT domain, which allows us to approximate any DCT graph filter by a MPGF, leading to a design with more degrees of freedom than the conventional PGF approach. Then, we extend those results to all of the 16 DTTs as well as their 2D versions, and show how their associated sets of multiple graph operators can be determined. We demonstrate experimentally that ideal low-pass and exponential DCT/DST filters can be approximated with higher accuracy with similar runtime complexity. Finally, we apply our method to transform-type selection in a video codec, AV1, where we demonstrate significant encoding time savings, with a negligible compression loss.