Graph-based Scalable Sampling of 3D Point Cloud Attributes

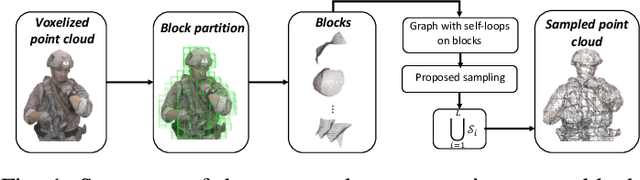
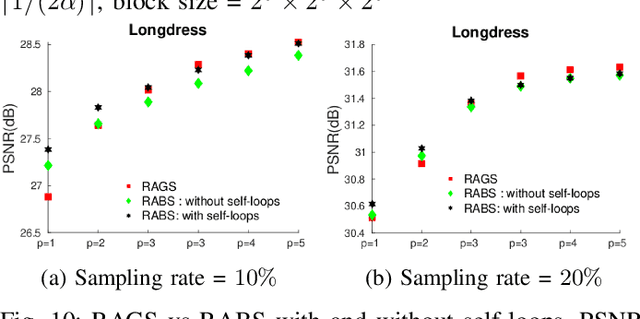
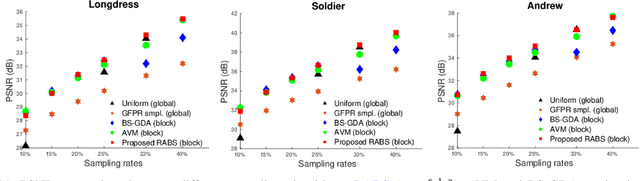
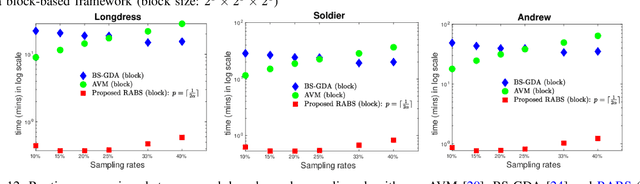
3D Point clouds (PCs) are commonly used to represent 3D scenes. They can have millions of points, making subsequent downstream tasks such as compression and streaming computationally expensive. PC sampling (selecting a subset of points) can be used to reduce complexity. Existing PC sampling algorithms focus on preserving geometry features and often do not scale to handle large PCs. In this work, we develop scalable graph-based sampling algorithms for PC color attributes, assuming the full geometry is available. Our sampling algorithms are optimized for a signal reconstruction method that minimizes the graph Laplacian quadratic form. We first develop a global sampling algorithm that can be applied to PCs with millions of points by exploiting sparsity and sampling rate adaptive parameter selection. Further, we propose a block-based sampling strategy where each block is sampled independently. We show that sampling the corresponding sub-graphs with optimally chosen self-loop weights (node weights) will produce a sampling set that approximates the results of global sampling while reducing complexity by an order of magnitude. Our empirical results on two large PC datasets show that our algorithms outperform the existing fast PC subsampling techniques (uniform and geometry feature preserving random sampling) by 2dB. Our algorithm is up to 50 times faster than existing graph signal sampling algorithms while providing better reconstruction accuracy. Finally, we illustrate the efficacy of PC attribute sampling within a compression scenario, showing that pre-compression sampling of PC attributes can lower the bitrate by 11% while having minimal effect on reconstruction.

Towards bandwidth estimation for graph signal reconstruction

In numerous graph signal processing applications, data is often missing for a variety of reasons, and predicting the missing data is essential. In this paper, we consider data on graphs modeled as bandlimited graph signals. Predicting or reconstructing the unknown signal values for such a model requires an estimate of the signal bandwidth. In this paper, we address the problem of estimating the reconstruction errors, minimizing which would thereby provide an estimate of the signal bandwidth. In doing so, we design a cross-validation approach needed for stable graph signal reconstruction and propose a method for estimating the reconstruction errors for different choices of signal bandwidth. Using this technique, we are able to estimate the reconstruction error on a variety of real-world graphs.

Practical graph signal sampling with log-linear size scaling

Graph signal sampling is the problem of selecting a subset of representative graph vertices whose values can be used to interpolate missing values on the remaining graph vertices. Optimizing the choice of sampling set can help minimize the effect of noise in the input signal. While many existing sampling set selection methods are computationally intensive because they require an eigendecomposition, existing eigendecompostion-free methods are still much slower than random sampling algorithms for large graphs. In this paper, we propose a sampling algorithm that can achieve speeds similar to random sampling, while reaching accuracy similar to existing eigendecomposition-free methods for a broad range of graph types.