Generalized Graph Signal Reconstruction via the Uncertainty Principle
Paper and Code
Sep 06, 2024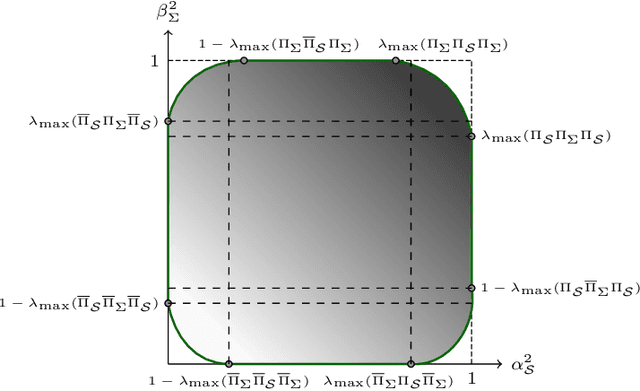
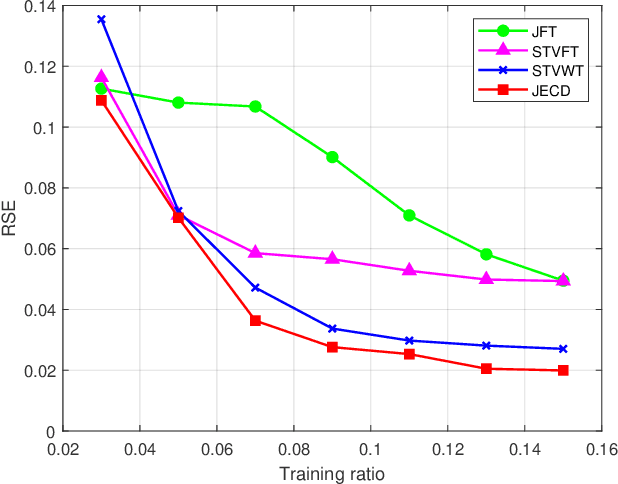
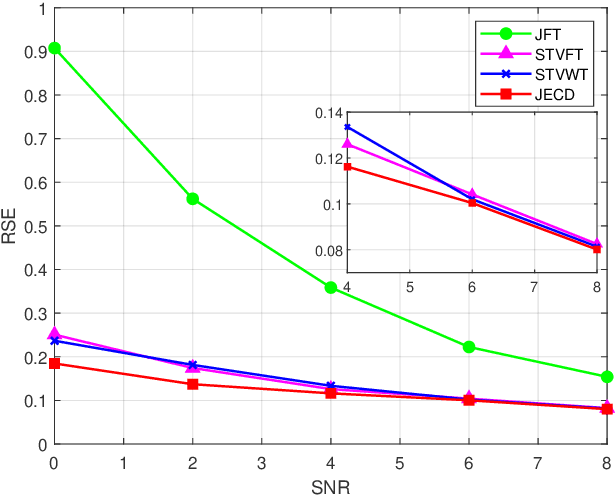
We introduce a novel uncertainty principle for generalized graph signals that extends classical time-frequency and graph uncertainty principles into a unified framework. By defining joint vertex-time and spectral-frequency spreads, we quantify signal localization across these domains, revealing a trade-off between them. This framework allows us to identify a class of signals with maximal energy concentration in both domains, forming the fundamental atoms for a new joint vertex-time dictionary. This dictionary enhances signal reconstruction under practical constraints, such as incomplete or intermittent data, commonly encountered in sensor and social networks. Numerical experiments on real-world datasets demonstrate the effectiveness of the proposed approach, showing improved reconstruction accuracy and noise robustness compared to existing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge