On Sampling of Multiple Correlated Stochastic Signals

Multiple stochastic signals possess inherent statistical correlations, yet conventional sampling methods that process each channel independently result in data redundancy. To leverage this correlation for efficient sampling, we model correlated channels as a linear combination of a smaller set of uncorrelated, wide-sense stationary latent sources. We establish a theoretical lower bound on the total sampling density for zero mean-square error reconstruction, proving it equals the ratio of the joint spectral bandwidth of latent sources to the number of correlated signal channels. We then develop a constructive multi-band sampling scheme that attains this bound. The proposed method operates via spectral partitioning of the latent sources, followed by spatio-temporal sampling and interpolation. Experiments on synthetic and real datasets confirm that our scheme achieves near-lossless reconstruction precisely at the theoretical sampling density, validating its efficiency.

Subset Random Sampling of Finite Time-vertex Graph Signals

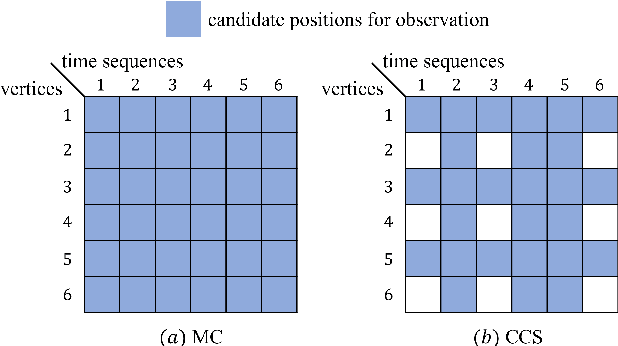
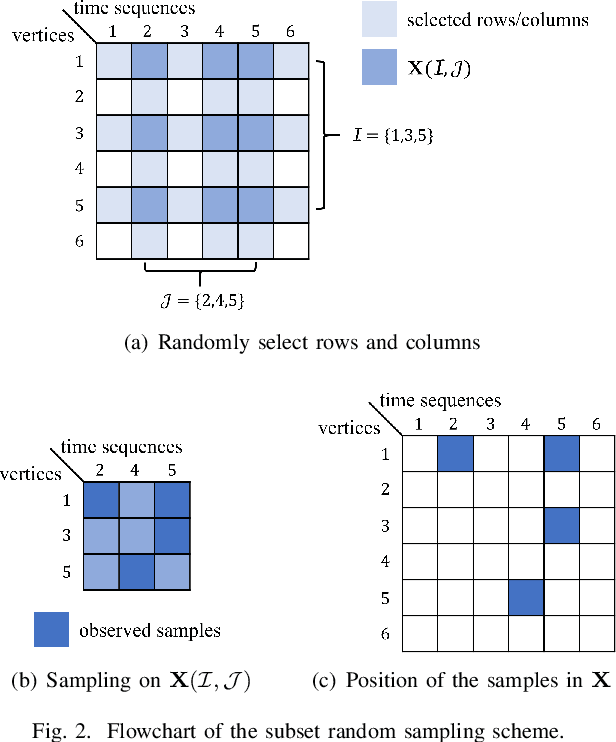
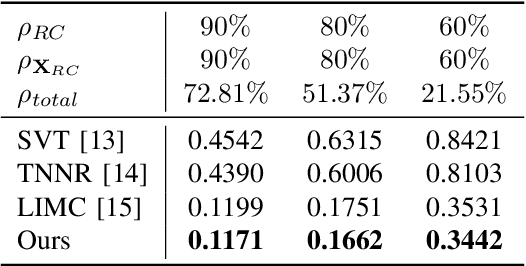
Time-varying data with irregular structures can be described by finite time-vertex graph signals (FTVGS), which represent potential temporal and spatial relationships among multiple sources. While sampling and corresponding reconstruction of FTVGS with known spectral support are well investigated, methods for the case of unknown spectral support remain underdeveloped. Existing random sampling schemes may acquire samples from any vertex at any time, which is uncommon in practical applications where sampling typically involves only a subset of vertices and time instants. In sight of this requirement, this paper proposes a subset random sampling scheme for FTVGS. We first randomly select some rows and columns of the FTVGS to form a submatrix, and then randomly sample within the submatrix. Theoretically, we prove sufficient conditions to ensure that the original FTVGS is reconstructed with high probability. Also, we validate the feasibility of reconstructing the original FTVGS by experiments.

The Transferability of Downsamped Sparse Graph Convolutional Networks

To accelerate the training of graph convolutional networks (GCNs) on real-world large-scale sparse graphs, downsampling methods are commonly employed as a preprocessing step. However, the effects of graph sparsity and topological structure on the transferability of downsampling methods have not been rigorously analyzed or theoretically guaranteed, particularly when the topological structure is affected by graph sparsity. In this paper, we introduce a novel downsampling method based on a sparse random graph model and derive an expected upper bound for the transfer error. Our findings show that smaller original graph sizes, higher expected average degrees, and increased sampling rates contribute to reducing this upper bound. Experimental results validate the theoretical predictions. By incorporating both sparsity and topological similarity into the model, this study establishes an upper bound on the transfer error for downsampling in the training of large-scale sparse graphs and provides insight into the influence of topological structure on transfer performance.

The Transferability of Downsampling Sparse Graph Convolutional Networks

In this paper, we propose a large-scale sparse graph downsampling method based on a sparse random graph model, which allows for the adjustment of different sparsity levels. We combine sparsity and topological similarity: the sparse graph model reduces the node connection probability as the graph size increases, while the downsampling method preserves a specific topological connection pattern during this change. Based on the downsampling method, we derive a theoretical transferability bound about downsampling sparse graph convolutional networks (GCNs), that higher sampling rates, greater average degree expectations, and smaller initial graph sizes lead to better downsampling transferability performance.

Sampling of Correlated Bandlimited Continuous Signals by Joint Time-vertex Graph Fourier Transform

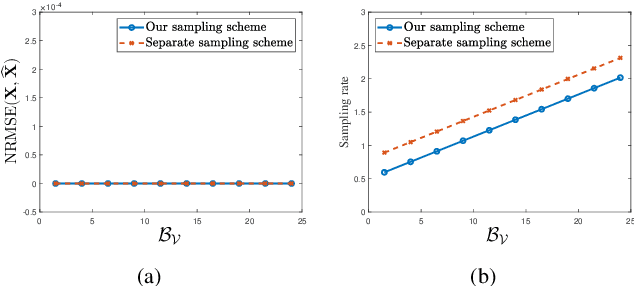
When sampling multiple signals, the correlation between the signals can be exploited to reduce the overall number of samples. In this paper, we study the sampling theory of multiple correlated signals, using correlation to sample them at the lowest sampling rate. Based on the correlation between signal sources, we model multiple continuous-time signals as continuous time-vertex graph signals. The graph signals are projected onto orthogonal bases to remove spatial correlation and reduce dimensions by graph Fourier transform. When the bandwidths of the original signals and the reduced dimension signals are given, we prove the minimum sampling rate required for recovery of the original signals, and propose a feasible sampling scheme.