Subset Random Sampling of Finite Time-vertex Graph Signals

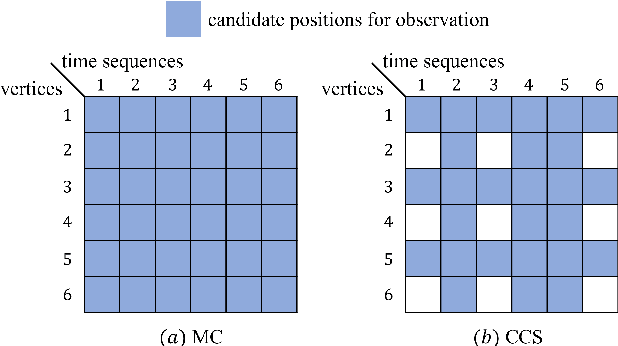
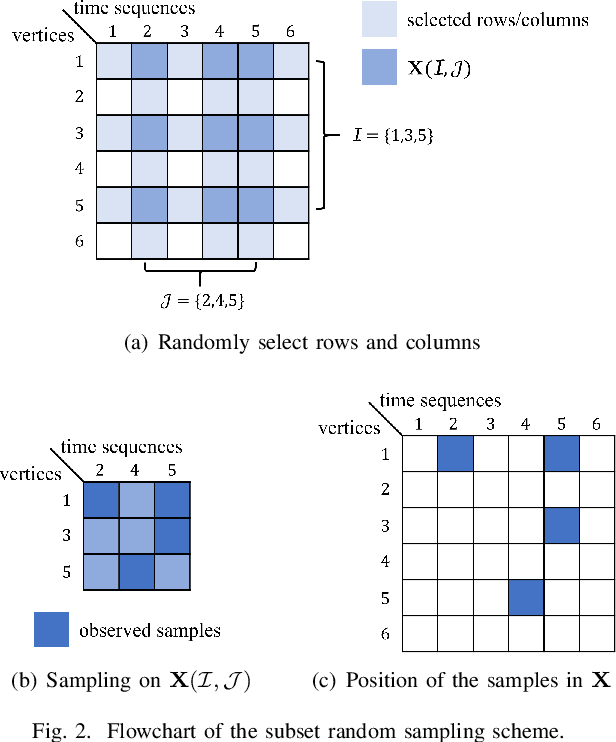
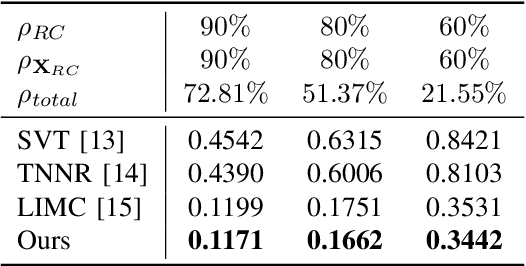
Time-varying data with irregular structures can be described by finite time-vertex graph signals (FTVGS), which represent potential temporal and spatial relationships among multiple sources. While sampling and corresponding reconstruction of FTVGS with known spectral support are well investigated, methods for the case of unknown spectral support remain underdeveloped. Existing random sampling schemes may acquire samples from any vertex at any time, which is uncommon in practical applications where sampling typically involves only a subset of vertices and time instants. In sight of this requirement, this paper proposes a subset random sampling scheme for FTVGS. We first randomly select some rows and columns of the FTVGS to form a submatrix, and then randomly sample within the submatrix. Theoretically, we prove sufficient conditions to ensure that the original FTVGS is reconstructed with high probability. Also, we validate the feasibility of reconstructing the original FTVGS by experiments.